5182. 【NOIP2017提高组模拟6.29】码灵鼠 (Standard IO)

peter_zhu01

于 2018-08-12 20:15:00 发布

阅读量78

点赞数

CC 4.0 BY-SA版权

本文链接：https://blog.youkuaiyun.com/peter_zhu01/article/details/84967266

本文介绍了一个有趣的数学问题：给定一个特殊的数列，如何计算第n项的期望值。通过对数列规律的研究，发现答案实际上非常简洁，即n+1。文中还提供了一段简单的实现代码。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Description

码零鼠是一只很喜欢mx数学的神犇，上面那个不是ta本人的样子。这天，ta在研究一个神奇的数列，这个数列是这样的：
a0 = 1
an = ai + aj (n>=1, i,j均在[0,n-1]内均匀随机)
Ta想知道对于给定的n，an的期望值是多少，你能告诉ta吗？
出于ta对整数的热爱，你只需要输出答案向下取整后的值

Input

一个整数T，表示数据组数
每组数据一行，包括一个整数n

Output

一个整数E(an)，

Solution

看到题解的你们可能吓一跳，我也不会。

但是通过打表，可以发现答案即为：n+1。

意不意外，什么规律都不用找耶。

非要知道Why的话，那......往下看↓

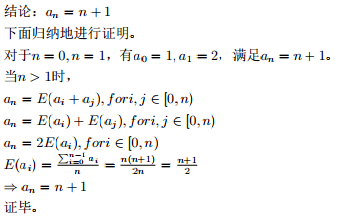
代码

还要看吗？

要？

那就看把......

 1 var
 2   n,t:longint;
 3 begin
 4   readln(t);
 5   while t>0 do
 6     begin
 7       readln(n);
 8       writeln(n+1);
 9       dec(t);
10     end;
11 end.