探秘C语言经典面试题“单身狗”，从此内存管理秒懂！-优快云博客

本文链接：https://blog.youkuaiyun.com/persevereX/article/details/149868939

一.引言

在算法面试和编程实践中，有一个经典而有趣的问题被程序员们亲切地称为 “单身狗” 问题。这类问题的核心是在一组数据中找出那些只出现特定次数的元素，就像在人群中找到独自徘徊的 “单身狗” 一样。今天，我们就来深入探讨其中两种经典的 “单身狗” 问题，并通过代码解析其背后的巧妙逻辑。

二.什么是“单身狗”问题？

单身狗1：在一个整数数组中，除了一个元素只出现一次外，其余元素都出现两次。找出只出现一次的那个元素。

例如数组中有：1 2 3 4 5 1 2 3 4，只有5出现一次，其他数字都出现2次，找出5。

单身狗2：在一个整数数组中，除了两个元素各自只出现一次外，其余元素都出现两次。找出这两个只出现一次的元素。

例如数组中有：1 2 3 4 5 1 2 3 4 6，只有5和6出现一次，其他数字都出现2次，找出5和6。

这类问题看似简单，但若想高效解决，却需要一些巧妙的思路！！！

三.核心思想：异或运算的性质

异或运算（XOR）是C语言中一种重要的位运算符，用于对整数数据的二进制位进行逻辑操作。其语法规则是：相同为0，不同为1。

a（二进制位）	b（二进制位）	a ^ b（运算结果）
0	0	0
0	1	1
1	0	1
1	1	0

①自反性：任何数和自身异或，结果是 0，即 a^a = 0。

例如3 ^ 3：0000 0011 ^ 0000 0011 = 0000 0000（显然自己和自己对应的每一位都相同，异或结果自然为0）。

②零元：任何数和 0 异或，结果仍是这个数，即 a^0 = a。

例如3 ^ 0：0000 0011 ^ 0000 0000 = 0000 0011（显然本身为0的位结果依然为0，本身为1的位结果依然为1）。

③交换律与结合律：异或运算满足交换律和结合律，可以任意变换操作顺序。

正是这些性质，让异或运算在解决 “单身狗”问题时易如反掌。

四.单身狗1详解

结合异或的性质，我们可以知道，若数组中只有一个"单身狗"，将所有元素依次异或，重复的成对元素互相抵消，最终得到的结果即为那个唯一元素。

#include <stdio.h>

int find_single_dog(int arr[], int sz)
{
    int ret = 0;
    int i = 0;
    for (i = 0; i < sz; i++)
    {
        ret ^= arr[i];
    }
    return ret;
}
int main()
{
    int arr[] = { 1,2,3,4,5,1,2,3,4 };
    int sz = sizeof(arr) / sizeof(arr[0]);
    int dog = find_single_dog(arr, sz);
    printf("%d\n", dog);


    return 0;
}

①时间复杂度O(n)

②空间复杂度O(1)

五.单身狗2详解

对于“单身狗2”来说因为存在两个只出现一次的元素，不能简单的将所有元素依次异或得到最终的结果。但是有没有什么办法可以把这个数组中的所有元素按某种规则分成两个子集，每个子集确保有且仅有一个“单身狗”元素。如图所示：

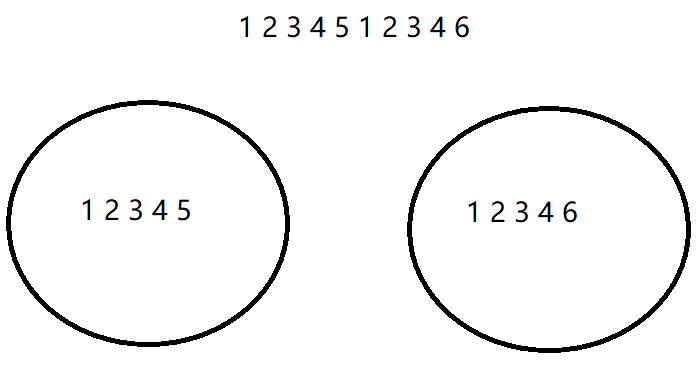
当我们按照某种规则将数组划分为两个子集合后，只需对每个子集合中的元素分别进行异或操作，就能分别得到那两个只出现一次的“单身狗”元素。

那么，究竟该如何划分这两个集合呢？我们知道，不同的整数在二进制表示上至少有一位不同。例如，5的二进制表示是 0000 0101，6的二进制表示是 0000 0110，它们在最低位（第1位）就不同。事实上，对于任意两个不同的整数，从第1位到第32位，它们一定在某一位（记为第k位）上是不同的。

因此，我们可以从第1位开始，逐位检查异或结果 num1 ^ num2，找到第一个为1的位置，即第k位。这个位置表示两个目标元素在该位上的值不同，可以据此将原数组划分为两个子集合：一组中该位为1，另一组中该位为0。

以示例中的5和6为例，它们在最低位上一个为1，一个为0，因此被分入不同的集合。而数组中其余的重复元素（如1、2、3、4、1、2、3、4）也会按照第k位的值分别归入两个集合中。由于这些元素都成对出现，在各自的集合内异或后会被抵消，最终每个集合中只会剩下一个唯一的“单身狗”，也就是我们要找的两个不同的数。

void FindNum(int arr[], int n, int* pnum1, int* pnum2)
{
	int ret = 0;
	int k = 0;
	for (int i = 0;i < n;i++)
	{
		ret ^= arr[i];
	}
	for (k = 0;k < 32;k++)
	{
		if (((ret >> k) & 1))
		{
			break;
		}
	}
	for (int i = 0;i < n;i++)
	{
		if ((arr[i] >> k) & 1)
		{
			*pnum1 ^= arr[i];
		}
		else
		{
			*pnum2 ^= arr[i];
		}
	}
}

int main()
{
	int arr[10] = { 1,2,3,4,5,1,2,3,4,6 };
	int n = sizeof(arr) / sizeof(arr[0]);
	int num1 = 0;
	int num2 = 0;
	FindNum(arr, n, &num1, &num2);
	printf("%d %d", num1, num2);
	return 0;
}

①时间复杂度：O(n)

②空间复杂度：O(1)

这就是C语言中“单身狗”问题的两种典型解法。通过异或运算的巧妙运用，我们不仅获得了简洁高效的实现，也学会了位运算的思维方式。希望对你理解位操作和优化算法有所帮助。