生物启发扑翼机设计与实现

生物启发飞行机器人的设计与开发

米卡埃尔·T·L·维埃拉、曼努埃尔·F·席尔瓦和费尔南多·J·费雷拉

1 引言

机器人领域一个活跃的研究与开发方向是生物启发式机器人的开发。无论是采用腿部、鳍还是机翼作为实现运动方式的机器人，其理念都是获取在数百万年进化过程中形成的生物的知识，并利用这些知识在所开发的机器上实现相同的运动方法（或至少采用生物启发式设计）。人们认为，通过这种方式，我们能够开发出在运动能力和能量效率方面具有与生物相似能力的机器。

研究飞行机器的先驱是列奥纳多·达·芬奇，大约在1490年，但直到这些机器能够成功实现之前，经历了漫长的发展过程。19世纪末期的首批项目成功实现了稳定飞行。

通过利用橡皮筋释放的弹性能量来驱动机翼的振荡运动。此后，项目开始采用蒸汽和压缩空气、人力发动机、内燃机，以及最近使用的电动机 [18] 进行开发。

目前存在多种扑翼机，例如SmartBird [4]、肖恩·金凯德 公园鹰 [6]、Cybird P1[5]和机器乌鸦 [2]。这些扑翼机采用轻质结构设计，同时具备高抗性，以应对飞行过程中所受的力以及可能因碰撞造成的冲击。此类机器的结构首选材料为碳纤维，以满足上述要求。为了实现稳定飞行并确保所需的升力，这些机器依赖于机翼与尾部之间的相互关系。通常由防撕裂尼龙和涤纶胶带制成的机翼负责产生推力，而尾部则负责机器的方向控制（影响方向和倾斜）。为了确保机翼在运动周期中具有不同的倾斜角度，这些设计将机翼分为两个区域：第一个区域固定在传动杆上，并始终保持绷紧；第二个区域由细小的碳棒组成，为第一区域提供直线性，同时作为机翼的弯曲部件，以被动方式获得机翼所需的角度。在电子系统方面，大多数此类机器人采用无刷电机和电子调速器（ESC）、锂聚合物（LiPo）电池为系统供电，两个伺服电机用于驱动尾部，以及一个接收器，用于将来自遥控器（RC）的信号传递至电机控制器。

在简要介绍之后，接下来的第二节介绍了生物的飞行原理。随后，第三和第四节分别介绍了扑翼机设计及其实现。第五节展示了为验证原型而进行的若干测试及获得的结果。最后，第六节总结了本工作的主要结论，并提出了一些关于扑翼机未来改进的想法。

2 生物的飞行

飞行过程中涉及四种力：升力（FL）、推力（FT）、阻力和重力。升力的垂直分量与自身质量产生的力方向相反，根据鸟类期望的运动状态，其中一个力应大于或小于另一个力。推力负责为生物体提供速度，并抵消作用在其上的阻力。

林顿[10]认为FL取决于机翼尺寸、飞行速度及其攻角(α)。增大 α会促进更大的FL（增加升力系数(CL)），但仅限于某一值之前，该值称为临界角（对大多数鸟类而言约为15°）。超过此值将产生湍流，导致阻力增大，从而使动物飞行所必需的速度丧失。鸟类的最大CL通常在1.5到1.7之间，对应于临界角的值。

机翼展弦比（AR）越高，临界角越低，但相反地，会提供更高的CL。

机翼的AR在小型鸟类中为4.8，在信天翁中为15[7]，其取决于两翼尖之间的总长度（b）和机翼面积（SW），依据如下：
$$
AR = \frac{b^2}{S_W}
$$
(1)

通过林顿提出的牛顿公式[9]，可以表述为CL与展弦比和 α之间存在如下表达式的关系：
$$
C_L = \frac{2\pi \times \alpha}{1 + \frac{2}{AR}}
$$
(2)

泰勒 et al [16]指出，动物在流体中以恒定速度运动时，斯特劳哈尔数 （σ）需保持在0.2至0.4之间。该参数将振幅A₀（相对于单个机翼尖端从最高点到最低点的长度，单位为米）与拍翅频率（f）以及给定的速度 v关联起来：
$$
\sigma = \frac{A_0 \times f}{v}
$$
(3)

FT是由翼膜的波动产生的。当机翼向上运动时，获得一个正的 α，而向下运动时则获得一个负的 α。该角度从翼根处的0°变化到翼尖处约22°或 −22°。简而言之，FT在翼根处几乎为零，在翼尖处达到最大值（负值或正值）。基于此，林顿[10]通过沿机翼长度的积分来获得FT。然后，通过另一个积分将鸟类的安装角(β)与沿机翼获得的 α值结合起来，林顿解释了FL是如何计算的。由于这两个力均产生于机翼的下拍阶段，而在上拍阶段不产生任何力，因此平均FT和FL由以下公式给出：
$$
F_{T,\text{MEAN}} = \frac{1}{6} \times \frac{2\pi}{1 + 2 \times AR} \times S_w \times \rho \times v^2 \times \sigma^2
$$
(4)
$$
F_{L,\text{MEAN}} = \frac{1}{4} \times \frac{2\pi}{1 + 2 \times AR} \times S_w \times \rho \times v^2 \times \beta
$$
(5)

2.1 动物飞行的生物力学

生物的翅膀通常由称为肱骨的膜带动。该膜与胸肌和上喙骨肌接触，这些肌肉发出移动翅膀所需的收缩力。胸肌主要负责下拍阶段。位于胸肌内侧的上喙骨肌连接到一条肌腱，该肌腱连接到肱骨顶部。该肌肉的收缩使肌腱带动肢体向上运动[17]。图1展示了这些肌肉如何促发特定的机翼运动。大多数研究项目都采用这种结构，用碳棒替代肱骨。

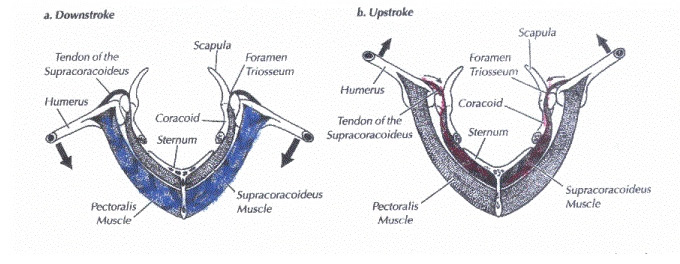
为了获得飞行所需的一定初始速度，生物具有腿部，在起飞时提供助力。因此，翅膀肌肉产生的能量消耗得以减少。此外，为了进一步减轻机翼的负担，当鸟类不拍打翅膀时，会采用两种飞行方式：滑翔和受限飞行[17]。为了实现转弯，鸟类通过胸肌进行不对称收缩，收缩程度较大的一侧即为鸟类滚转的方向。该动作在从头部到尾部的纵轴上产生力矩。这种称为滚转的动作意味着身体的旋转。鸟类的尾部提供飞行稳定性，并影响升力和阻力。通过特定的倾斜角度，可以促进获得期望升力运动的更佳 α值，而较长尾部引起的较大阻力则有助于提高横向稳定性。

2.2 翅膀

根据康奈尔鸟类学实验室的说法，鸟类翅膀有四种类型[12]：被动滑翔、主动滑翔、椭圆形和高速。每种类型都具有一些特定的飞行特性[3]。

机翼设计中的一个重要参数是机翼载荷（WL），它反映了单位面积所支撑的质量[15]。通常，WL的范围在1至20 kg/m²之间，据估计鸟类的最大允许值为25 kg/m²[8]。WL值较大的鸟类相比其他鸟类具有更高的最高速度，但需要更长的距离进行着陆和起飞，且机动更加困难。

3 原型设计

3.1 动物翅膀研究与扑翼机参考参数

实现扑翼机的第一个要点是确定所使用的机翼类型及其参数。本项目选择了椭圆翅膀（类似于蝙蝠和麻雀的翅膀）。这一特点可降低操控机翼所需的扭矩，采用较小的展弦比，并提供更好的飞行控制能力。为了验证此信息，收集了7种鸟类[13][14]和23种蝙蝠[1]的数据，它们均具有椭圆翅膀，以确定展弦比是否接近最小值4.8。事实上，蝙蝠的平均值为6.3，而七种鸟类的平均值为8.6。还进行了计算以验证WL是否在[1；20] kg/m²范围内。蝙蝠的平均值为0.69 kg/m²，七种鸟类的平均值为6.02 kg/m²。可以得出结论，该范围不适用于蝙蝠，但适用于彭尼奎克研究中的所有鸟类[13][14]。这7种鸟类和23种蝙蝠样本的平均WL为0.97 kg/m²。该值与其他项目中使用的数值相近，例如肖恩·金凯德 公园鹰（1.65 kg/m²）[6]和赛鸟P1（0.82 kg/m²）[5]。因此，这些项目的机翼设计似乎以蝙蝠为灵感来源。

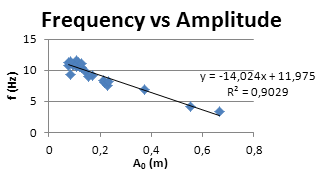
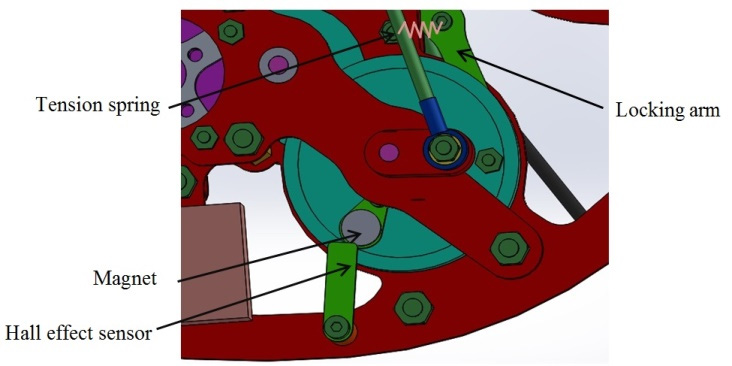
考虑到这些因素，可以利用蝙蝠作为样本，找出飞行中涉及的某些变量之间存在的一些相互依赖关系。图2(a)显示了蝙蝠WL与其质量之间存在0.92的强相关性。巴伦和麦肯齐[1]发现频率f与蝙蝠质量之间的相关性在0.748到0.905之间变化，并且这三个表达式因飞行速度不同而不同。结合上述其他研究，可以验证f与蝙蝠质量相关，如图2(b)所示。为了实现稳定飞行，σ必须处于一定范围的值内。这表明振幅与f相互关联，如图2(c)所示，其中得到的相关性为0.903。还可以绘制出翼展与SW之间的相关性。尽管面积依赖于翼展值，但图2(d)显示机翼始终遵循相同的椭圆形状。

通过对蝙蝠飞行的研究，可以根据扑翼机的质量确定其必须具备的参数。使用SolidWorks 2013计算机辅助设计软件，设计了一台质量为0.593千克的机器。该值反映了表1中所示的参考参数。

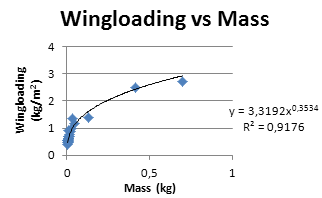WL与蝙蝠质量，(b) f与蝙蝠质量，(c) f与蝙蝠的翼振幅，以及(d) SW与蝙蝠机翼的翼展。)

参数	值	Unit	表达式
Mass	0.593	kg	-
机翼载荷 (WL)	2.760	千克/米²	3.3192·米⁰.³⁵³⁴
机翼面积 (SW)	0.215	m²	m / WL
翼展 (b)	1.264	m	2.8417·Sw⁰.⁵²⁶⁸
展弦比 (AR)	7.436	-	b² / SW
扑翼频率（f）	4.126	Hz	3.6814·米⁻⁰.²¹⁸
振幅（A₀）	0.560	m	频率⁻¹¹.⁹⁷⁵ / ⁻¹⁴.⁰²⁴
振幅角	52.56	度	Arcsen(2·(A₀/2)/(b/2))

3.2 扑翼机电子架构

电子元件的选择与机器的设计同步进行，因为它们会影响机器的重量。电源由两个锂聚合物电池提供，在使用无刷电机时性能充足，重量轻，容量为1300毫安时，电压为7.4伏特。电机包括两个伺服电机HD-1160A（用于尾部方向控制）和一个800千伏的无刷电机Sunnysky Angel A2212（负责机翼循环运动）。

该无刷电机提供所需扭矩，但为了实现从7.4伏特到5伏特的电压调节、直流转交流转换以及将PWM信号转化为电机转速，采用了Turnigy Plush 30 A电子调速器。通信方面采用预编程的6通道接收器与遥控控制器配合使用。该接收器工作电压为5伏特，由电子调速器供电。

当机翼无扭矩输入时，扑翼机必须能够滑翔。为此，在末级齿轮中安装了一块磁铁，并使用霍尔效应传感器，以确保机翼停在指定位置。该功能由 Arduino Nano实现，用于处理传感器提供的脉冲，作为接收器与电子调速器之间的中间件，从而将无刷电机停在指定位置。

3.3 扑翼机机械设计

机翼由防撕裂尼龙以及有粘性和无粘性达克龙胶带构成。由于机翼执行的循环运动与机器本身并非线性相关，因此采用球铰通过垂直轴连接来传递动力。这样，后部和前部的碳棒均能实现机翼所需的运动。机翼设计为产生0.56米的振幅，角度为55.2度角（28.4度向上和23.8度向下）。用于动力传递的碳棒直径为3毫米，其提供的屈服强度远高于理论上施加于它们的应力。

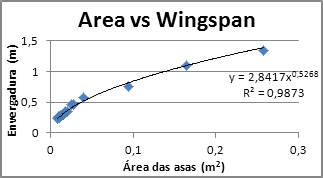
扭矩减速系统采用模数0.8的德尔林齿轮，从电机到末级齿轮实现13.3:1的减速比。该系统基于主框架和两个通过螺纹固定片保持与主框架恒定距离的部件构成。电机旋转方向至关重要，因为机翼在下降运动期间应比上升运动时具有更快的速度。下拍阶段设计为179度，上拍阶段为181度。图3(a)展示了在使用垂直轴系统时，这如何影响旋转方向。无刷电机的施加扭矩为0.046牛·米。为克服此扭矩，预计需要4.13安培电流。为了获得所需f = 4，计算出1赫兹时电流为4.4安培，而电机的最大允许电流为10安培。

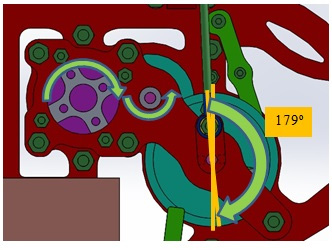
为了补充由霍尔效应传感器执行的锁定系统，该部件被集成到一个机械锁臂中，并在最后一个齿轮上设有弹簧，以防止电机无法承受施加扭矩时进入滑翔飞行位置。图3(b)展示了该系统的实现方式。一旦传感器指示机翼停止位置，由于拉伸弹簧作用，齿轮内置螺钉会与锁臂对齐。此时，由于机器将向下运动在重力作用下运动时，机翼会因风的作用而向上移动，此时螺栓固定在臂上。

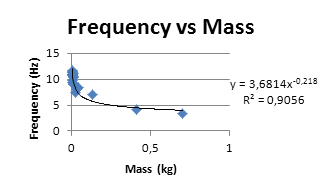
图3(c)展示了伺服电机如何工作以实现尾部运动。伺服电机1负责控制尾部的方向，其功能是将尾部施加的力的垂直分量移向一侧，从而在纵轴上产生力矩。该扭矩形成飞行过程中转弯所需的滚转运动。该伺服电机与尾部之间的中间部分应确保一定的倾斜角度，以促进碗形轨迹，并保持由另一个伺服电机设定的攻角。伺服电机2负责调节第一个伺服电机的倾斜角度，以获得机器所需的攻角。

尾翼面积为1.31 平方分米²，伺服电机提供的最大扭矩为2.0 千克·厘米。这些计算很难精确进行，因为它们依赖于空气阻力产生的阻力系数，而该参数通常通过实验获得。然而，在一种极端情况下进行了计算，其中阻力系数取值为0.67（通过迭代得到的值），气流速度为11.5 米/秒。在这种特定情况下，确定在舵机升降装置施加的最大扭矩下，尾部的最大面积为3.8 平方分米²。

主框架负责支撑扑翼机中的所有部件，并设计为便于这些部件的快速组装。其前部安装减速箱，中部放置电子元件，后部安装用于驱动尾部的伺服电机，上方则安装机翼。该机器的质心（CoM）应位于机翼长度的1/3至1/4处，沿纵轴方向。该部分设计的主要挑战在于如何将各部件向前布置，并将此位置与机翼的位置进行协调比较。

在机器上，该质心理论上位于机翼长度的0.319处。在此2毫米厚的框架内，质心位于其中一个表面1.2毫米的位置。图4(a)和4(b)显示了该质心的位置。

4 原型的实现

机翼和尾部结构采用防撕裂尼龙制成，通过涤纶胶带和3M VHB双面胶带固定到机械结构上。使用VHB双面胶带时，首先将非粘性涤纶胶带（图5(a)中的蓝色胶带）嵌入机翼中，形成用于插入碳棒的“袋状结构”。随后将小型碳棒插入其中，并利用双面VHB胶带将其固定，再用小条防撕裂尼龙覆盖，以形成机翼的波动区域。最后阶段，使用粘性涤纶胶带（图5(b)中所示的黑色胶带）加固非粘性胶带的固定部分。机翼单独制作，最后连接在一起。在该连接处，使用非粘性涤纶胶带和双面VHB胶带在机翼中心形成一个“袋状结构”，其功能类似于人体的脊柱（见图5(c)）。图6(a)标识了插入此中央口袋的部分。该区域也使用粘性涤纶胶带来加强机翼之间的连接。尾部采用相同的构造方法。使用四根直径为1毫米的杆，确保尾部始终沿垂直方向（从图6(b)视角）伸展，并在主杆两侧的双面胶带层中固定一根从一侧弯向另一侧的弯曲杆。

使用胶粘剂也为此项目带来了优势。对于机翼和尾部，杆与相应连接件之间需要一种具有较强强度且具有一定延展性的连接。这些连接采用 SikaForce 7752 FRW L60。用于传动箱中轴承的固定时，使用乐泰603，可确保接触部件之间的径向固定。

机械结构部件（如图6(c)所示）所用材料为5083铝合金，通过激光切割、水射流切割和折弯加工而成。

机械锁臂需要处于固定位置，同时也能自由旋转。通过使用带翻边衬套，并利用垫圈将该部件置于所需位置，再通过穿过衬套中心的螺钉实现永久固定。锁定系统中的传感器发送信号需要几微秒的时间，因此其位置应可调节，以确保在固定螺栓穿过锁臂后机翼立即停止运动。

为了控制扑翼机，开发了一个程序，使Arduino Nano作为接收器、霍尔效应传感器和电子调速器（连接至电机）之间的中间件。Arduino控制器每20毫秒读取一次来自遥控控制器的值，以计算需要执行的操作。遥控控制器传输的PWM信号在1.1和1.7毫秒之间变化（已确认机器在1.7毫秒时显示最大频率为5赫兹），在此情况下，当推子低于1.35毫秒时，向电子调速器发出指令，使其输出1.40毫秒的信号，直到霍尔效应传感器检测到非零值，此时命令电机停止。在实现机器的期望运行后，进行了整体组装（图7）。

5 测试执行和结果达成

最初确定了机器的总质量。由于防撕裂尼龙的密度为56克/米²，机翼面积为0.215米²，因此该部件的质量预计为12克。然而，机翼和尾部的预期质量与实际质量存在差异。建造完成后，经核实其重量约为45克。这是因为在波动区域加入了直径为1毫米的杆、涤纶胶带以及VHB双面胶带所致。这一因素解释了预期质量0.593千克与实际值0.647千克之间的差异。然而，为此重量确定的值，例如f和SW，与所实现原型的实际测量值之间并无显著差异。

为了确定产生的FT，将扑翼机通过一根绳子悬挂起来，并使其与质心对齐，同时用两根绳子从侧面固定，以确保FT仅在前进方向上产生。另外，从机器后部连接一根绳子到测力计。该测力计使用一根木杆来帮助测力计与扑翼机之间的对齐。测力计测得的数值会波动，因为扑翼机仅在机翼向下运动时才产生FT，但在频率为f = 5赫兹、振幅为0.55米时，记录到的峰值在1至2牛之间。这些数值接近通过林顿[10]给出的表达式计算出的理论值（FT = 1.31 N）。

为了了解该机器是否能够施加持续飞行所需的FL，使用了一根与扑翼机质心对齐的绳子。该测试通过将扑翼机沿圆形路径投掷（圆心为绳子上端固定点），并观察其能否实现稳定飞行。由于绳子刚性较大，其产生的张力最终会影响扑翼机的稳定性。因此，实验改用弹性绳重复进行，但弹性绳无法保证圆形路径，并且最终也会影响飞行中的力。实验未使用测量仪器对FL进行量化，但结论表明该机器无法施加使其升空所需的力。

6 结论与未来发展

本文描述了一种扑翼机的设计与开发。其构造表明，在设计阶段不易察觉的一些细节确实存在。结构的机械行为符合预期。伺服电机能够传递必要的力，以将尾部稳定在固定位置，而无刷电机确保提供f = 5赫兹的频率。通过悬吊测试可知，质心位于预期位置。3毫米直径杆具有良好的抗弯强度，并确保扭矩传递。电子系统工作正常且尺寸设计合理。该系统的局限性在于PWM信号在1.1和1.7毫秒之间的传输范围。若增加投入，可获得符合预期1到2毫秒范围的遥控控制器。因此可以获得更大的FT并实现更高速度，有利于提高FL。

根据所进行的测试，可以得出结论：FT 的期望值在实验结果范围内，并且它取决于f。林顿也证实了这一信息，因为他指出该力取决于f、振幅和机翼尺寸，而FL 则取决于飞行速度、机翼尺寸和α。因此，在扑翼机设计中，可以通过制造具有较佳表面积的机翼来改善性能，但需始终考虑σ和AR的值。这样，在这些条件下，扑翼机产生所需升力时可采用较低的速度或f值。