面试顺序问题的Matlab和Lingo解法

本文lingo解法来源[1]。

1 面试顺序问题

有 4 名同学到一家公司参加三个阶段的面试：公司要求每个同学都必须首先 找公司秘书初试，然后到部门主管处复试，最后到经理处参加面试，并且不允许插队（即 在任何一个阶段 4 名同学的顺序是一样的）。由于 4 名同学的专业背景不同，所以每人 在三个阶段的面试时间也不同，如下表所示。这 4 名同学约定他们全部面试完以后一起离开公司。假定现在时间是早晨 8:00，请问他们最早何时能离开公司？

	秘书初试	主管复试	经理面试
同学甲	13	15	20
同学乙	10	20	18
同学丙	20	16	10
同学丁	8	10	15

2 建立模型

实际上，这个问题就是要安排 4 名同学的面试顺序，使完成全部面试所花费的时间最少。
记$t_{ij}$为第i名同学参加第 j 阶段面试需要的时间（已知），令$x_{ij}$表示第i名同学参加第j阶段面试的开始时间（不妨记早上 8:00 面试开始为 0 时刻） （i=1,2,3,4 ; j =1,2,3），T 为完成全部面试所花费的最少时间。
优化目标：
min ⁡ { T } = { [ max ⁡ i   ( x i 3 + t i 3 ) ] } \min \left\{ T \right\}=\left\{ \left[ \underset{i}{\mathop{\max }}\,\left( {{x}_{i3}}+{{t}_{i3}} \right) \right] \right\} min{T}={[imax​(xi3​+ti3​)]} （1）

约束条件：
1） 时间先后次序约束（每人只有参加完前一个阶段的面试后才能进入下一个阶段）：
$x_{ij}+t_{ij}\le x_{i,j+1},i=1,2,3,4,j=1,2$
2） 每个阶段j同一时间只能面试1名同学：用0−1变量$y_{ik}$表示第k名同学是否排在第i名同学前面（1 表示“是”，0 表示“否”）。

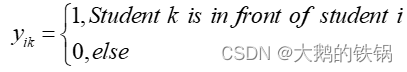
参考文献[1]中此处比较简略，本文按笔者理解较为详细阐述。
例如，当i=1，k=2时，y₁₂=1表示第2个同学在第1个同学前面，y₁₂=0表示第1个同学在第2个同学前面，假定此时是第一次面试j=1。
按照y₁₂=1和y₁₂=0分别画出时间线图：

图1 y~12~=1

图2 y~12~=0

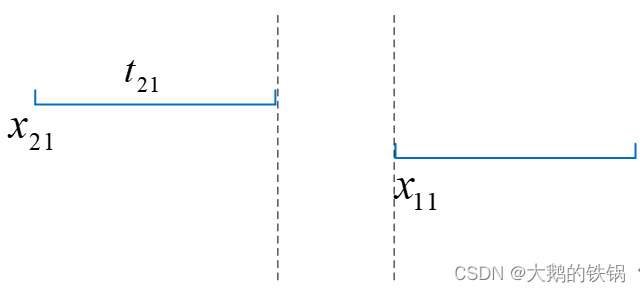
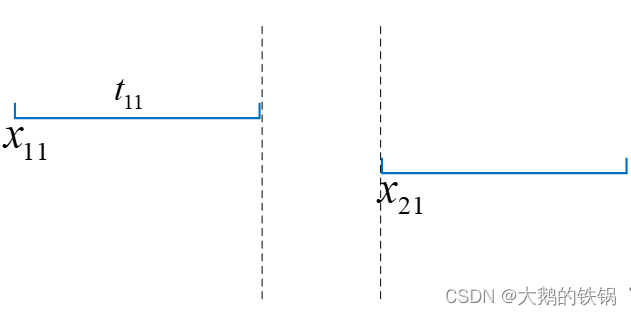
上述两种情况分别需要满足：

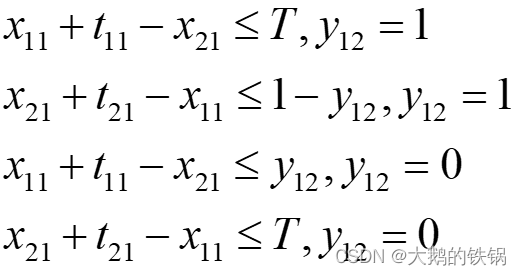
上式可以写为：

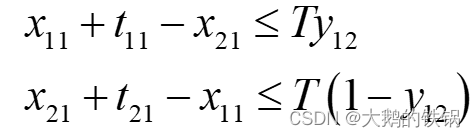
所以第二个约束条件为

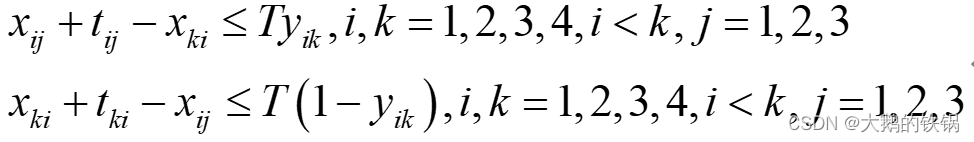
上式是一个非线性约束条件，可以将T写为一个较大常数M，转化为线性约束。
3） 非线性的优化目标改写成如下线性优化目标

4） 所有变量的非负约束和$y_{ik}$的0-1约束。

3 模型求解

3.1 Lingo求解

程序：

model:
Title 面试问题; 
SETS: Person/1..4/; 
Stage/1..3/; 
PXS(Person,Stage): T, X; 
PXP(Person,Person)|&1 #LT# &2: Y; 
ENDSETS 
DATA: 
T=13, 15, 20, 10 , 20 , 18, 20, 16, 10, 8, 10, 15; 
ENDDATA 
[obj] min=MAXT; 
MAXT>= @max(PXS(i,j)|j#EQ#@size(stage):x(i,j)+t(i,j)); 
! 只有参加完前一个阶段的面试后才能进入下一个阶段; 
@for(PXS(i,j)|j#LT#@size(stage):[ORDER]x(i,j)+t(i,j)<x(i,j+1)); 
! 同一时间只能面试1名同学; 
@for(Stage(j):   
    @for(PXP(i,k):[SORT1]x(i,j)+t(i,j)-x(k,j)<MAXT*Y(i,k));  
    @for(PXP(i,k):[SORT2]x(k,j)+t(k,j)-x(i,j)<MAXT*(1-Y(i,k)))); 
@for(PXP: @bin(y)); 
end

结果：所有面试完成至少需要 84min，面试顺序为 4－1－2－3（丁－甲－ 乙－丙）。早上 8:00 面试开始，最早 9:24 面试可以全部结束。

3.2 Matlab求解

程序：

% 面试顺序问题matlab程序
clear;clc;close all;
%% 输入数据
t = [13, 15, 20;
    10, 20, 18;
    20, 16, 10;
    8, 10, 15];
A = zeros(20,19);
b  = zeros(19,1);
M = sum(sum(t)); % M设置为所有同学总计约束时间
cnt = 1;
%% 约束条件
% 约束1
for loop1 = 1:8
    for loop2 = 1:2
        A(loop1, (ceil(loop1/2)-1)*3+mod(loop1,2)*-1+2) = 1;
        A(loop1, (ceil(loop1/2)-1)*3+mod(loop1,2)*-1+3) = -1;
        b(loop1) = -1*t(ceil(loop1/2), mod(loop1,2)*-1+2);
    end
end
% 约束2
for loopk = 3:4
    for loopi = 1:loopk-1
        for loopj = 1:3
            if loopk == 3
                temp = 1;
            else
                temp =3;
            end
            A(8+cnt,(loopi-1)*3+loopj) = 1;
            A(8+cnt,(loopk-1)*3+loopj) = -1;
            A(8+cnt,12+temp+loopi) = -1*M;
            b(8+cnt) = -1*t(loopi,loopj);
            A(9+cnt,(loopk-1)*3+loopj) = 1;
            A(9+cnt,(loopi-1)*3+loopj) = -1;
            A(9+cnt,12+temp+loopi) = M;
            b(9+cnt) = -1*t(loopk, loopj)+M;
            cnt = cnt+2;
        end
    end
end
sizeA = size(A,1);
cnt = 1;
for loopj = 1:3
     % k=2,i=1
    A(sizeA+cnt,loopj) =1; A(sizeA+cnt,3+loopj) =-1;   A(sizeA+cnt,13) =-1*M;     
    b(sizeA+cnt)  = -1*t(1,loopj); 
    A(sizeA+cnt+1,loopj) = -1; A(sizeA+cnt+1,3+loopj) =1; A(sizeA+cnt+1,13) = M;     
    b(sizeA+cnt+1)  = M-1*t(2,loopj);
    cnt = cnt+2;
end
% 约束3
sizeA = size(A,1);
for loopi = 1:4
    A(sizeA+loopi,(loopi-1)*3+3) = 1;
    A(sizeA+loopi,19) = -1;
    b(sizeA+loopi) = -1*t(loopi,3);
end
% 边界约束
lb = zeros(19,1);
ub = inf(19,1); ub(13:18) = 1;
intcon = 1:19;
%% 目标函数
f = zeros(19,1); f(19) = 1;
%% 优化
options = optimoptions('intlinprog','Display','off');
[x,fval,exitflag,output] = intlinprog(f,intcon,A,b,[],[],lb,ub,[],options);
if exitflag==1 && fval==M
    disp('find');
    x_opt = x;
    fval_opt = fval;
end
x
fval

计算结果为：
8 21 36 21 36 56 31 58 74 0 8 18 0 0 0 1 1 1 84
对应19个决策变量，分别为
$x_1\sim x_{12}:$每名学生面试开始时间；
$x_{13}\sim x_{18}:$第k名同学是否在第i名前面，分别为第2名同学是否在第1名同学前面，3是否在1、2前面，4是否在1、2、3前面；
$x_{19}:$全部面试所花费的最少时间。
所以，所有面试完成至少需要 84min，面试顺序为 4－1－2－3（丁－甲－ 乙－丙）。早上 8:00 面试开始，最早 9:24 面试可以全部结束。

4 总结

1、0-1变量$y_{ik}$的引入。
2、非线性约束的线性化，T写为一个较大常数M。
3、目标函数中包含max时的处理。

参考文献：
[1]: 司守奎. 数学建模算法与程序[M]. 国防工业出版社，2013.