刷题笔记-蘑菇阵

最新推荐文章于 2022-06-05 10:30:00 发布

转载最新推荐文章于 2022-06-05 10:30:00 发布 · 217 阅读

CC 4.0 BY-SA版权

原文链接：https://blog.youkuaiyun.com/yl_puyu/article/details/103185429?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522162669709016780264087257%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=162669709016780264087257&biz_id=0&

算法刷题专栏收录该内容

7 篇文章

订阅专栏

该博客介绍了一道概率计算题目，A和B在蘑菇阵中，A从起点(1,1)随机向B( n, m )移动，求避开蘑菇到达B家的概率。通过动态规划方法，利用概率转移来计算每个位置避开蘑菇的概率，最终得出结果。文章讲解了代码实现，包括概率矩阵的初始化和转移概率的计算，并给出了C++代码示例。

1. 题目来源
链接：蘑菇阵
来源：牛客网

2. 题目说明

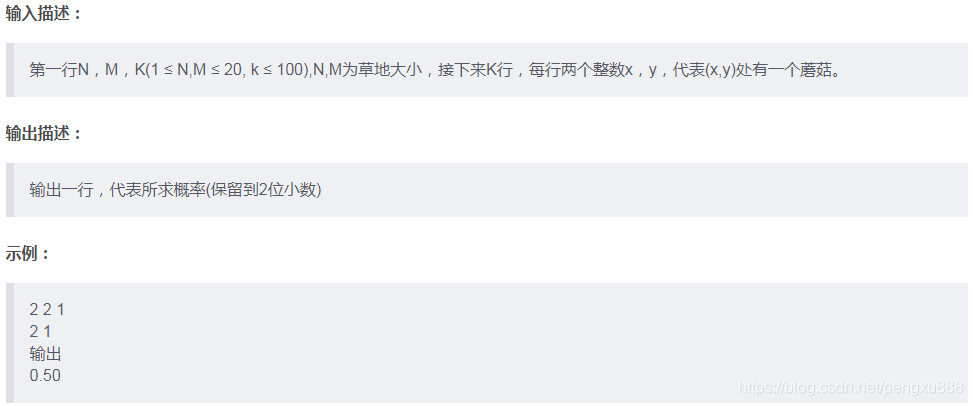
现在有两个好友A和B，住在一片长有蘑菇的由n＊m个方格组成的草地，A在(1,1),B在(n,m)。现在A想要拜访B，由于她只想去B的家，所以每次她只会走(i,j+1)或(i+1,j)这样的路线，在草地上有k个蘑菇种在格子里(多个蘑菇可能在同一方格),问：A如果每一步随机选择的话(若她在边界上，则只有一种选择)，那么她不碰到蘑菇走到B的家的概率是多少？

在这里插入图片描述

3. 题目解析

题意很明确，就是区域dp。将原矩阵各个元素转化为概率，直接进行概率运算即可。由于A只能往右、下走，故当其不在边界时会有常规的两种走法，而当其位置在边界位置时，只会有一种走法，这时踩到蘑菇的概率会由0.5—>1 起点概率设置为1，有蘑菇的位置概率设置为0。最后输出2位小数，注意fixed、setprecision()的函数使用，忘记拼写的话…printf（%.2f，p[n][m]）也能派上用场。

常见误区：
在这里插入图片描述

4. 代码展示

#include <bits/stdc++.h>

using namespace std;
int main() {
    int n, m , k;
    while (cin >> n >> m >> k) {
        vector<vector<int>> table((n + 1), vector<int>(m + 1));  // 记录蘑菇
        vector<vector<double>> p((n + 1), vector<double>(m + 1));  // p[i][j]表示不碰到蘑菇走到i,j的概率
        int x, y;
        for (int i = 0; i < k; ++i) {
            cin >> x >> y;
            table[x][y] = 1;
        }
        p[1][1] = 1.0;  // 起点概率为1
        for (int i = 1; i <= n; ++i) {
            for (int j = 1; j <= m; ++j) {
                if (!(i == 1 && j == 1)) {  // 跳过起点
                    p[i][j] = p[i - 1][j] * (j == m ? 1 : 0.5) + p[i][j - 1] * (i == n ? 1 : 0.5);  // 边界的时候，概率为1
                    if (table[i][j] == 1)
                        p[i][j] = 0;  // 如果该点有蘑菇，概率置为0
                    
                }
            }
        }
        cout << fixed << setprecision(2) << p[n][m] << endl;
    }
    return 0;
}
————————————————
版权声明：本文为优快云博主「Ypuyu」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.youkuaiyun.com/yl_puyu/article/details/103185429