单词的含义
如何定义一个单词的意思?通过韦伯字典对于单词”meaning"的解释来看,有如下几点
- 单词或者短语呈现的意思。
- 人想要通过短语、符号表达的实际含义。
- 文章、艺术作品呈现的想法。
故最普通对meaning的理解,其实是表示符号(symbol)向想法(idea)的转换。
如何在计算机中计算语义。可以使用,wordnet,一个包含同义词集合和词间关系的词库。

但是WordNet仍有缺点,如下
- 缺少语境信息。如"proficient"被列为"good"的同义词,但这其实只在特定语境情况下满足。
- 缺少新派生的单词,不可能一直保持更新。
- 有一定偏见性。
- 需要人来进行适配。
- 不能精确的计算词语的相似性。
在传统的NLP中,我们把单词看作为离散的变量,如hotel, conference, motel这三个词使用one-hot(独热)均做局部表示,

但是这种表示方法,有很大的缺点,对于任意两个单词,他们之间是正交的,即没有办法计算任意两个单词之间的相似度。
分布式语义表示
一个单词的语义由其经常出现的周围的单词表示。对与一个单词w,他的上下文是固定大小的窗口附近的单词,并且使用这个窗口内的单词来表示中心词w.

之后,我们将会为每一个单词构建一个稠密向量,以便出现在相似上下文中的单词向量也相似。通常这个word vector被叫做word embedding(单词嵌入)或者word representations(单词表示)。他们都是分布式表示。
Word2vec
Word2vec的基本思想
Word2vec是一个学习单词向量的框架,其基本思想如下:
- 已经拥有包含大量文本的语料库。
- 在固定单词表中的每一个单词都将被表示为向量形式。
- 遍历文本的每一个位置ttt,每遍历一个位置,将其分为中心词ccc和上下文词ooo。(使用滑动窗口,滑动窗口中心为中心词,其余词作为上下文词)
- 使用中心词ccc和上下文词ooo的词向量相似度来计算已知ccc出现ooo的概率,即P(o∣c)P(o|c)P(o∣c)(反过来也可以)。
- 随着遍历位置的变化,不断调整词向量,使得条件概率最大化。
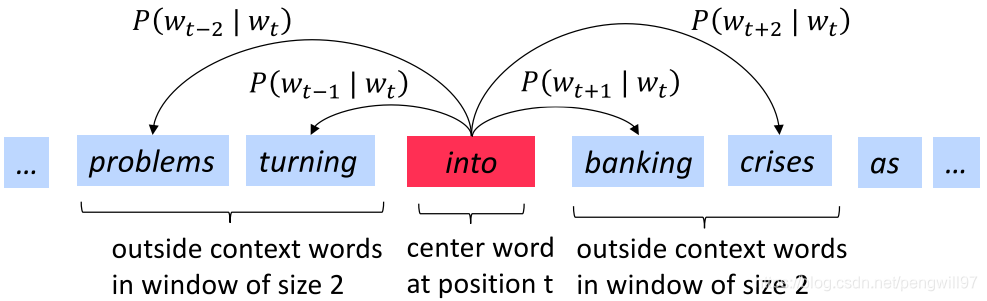
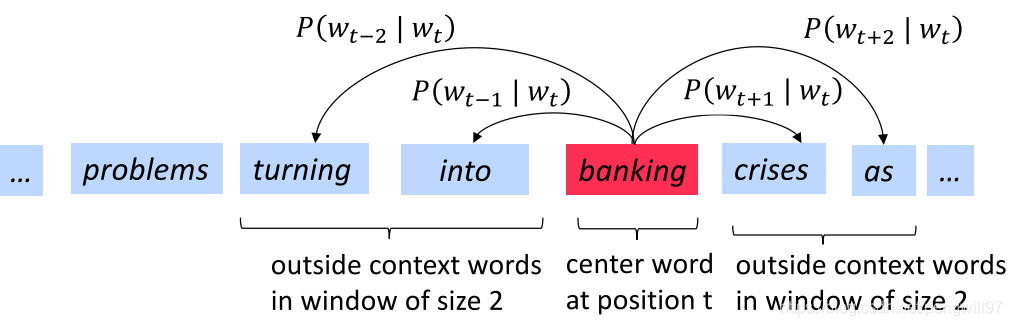
Word2vec的目标函数
对于一个位置t=1...Tt=1...Tt=1...T,使用长度固定为mmm的滑动窗口,在已知中心词的情况下预测上下文wjw_jwj。
Likelihood=L(θ)=∏t=1T∏−m≤j≤m,j≠0P(wt+j∣wt;θ)
Likelihood=L(\theta)=\prod_{t=1}^{T}\prod_{-m\le j \le m, j\ne 0} P(w_{t+j}|w_t;\theta)
Likelihood=L(θ)=t=1∏T−m≤j≤m,j=0∏P(wt+j∣wt;θ)
其中θ\thetaθ是所有待优化变量。上式即,对于每一个中心词wtw_twt,求出对每一个上下文词wt+jw_{t+j}wt+j的条件概率,做乘积做似然函数。由于连乘积很容易太小,这样导致求解不易,通常取logloglog处理;另外一般对目标函数求最小,故求负;最后对TTT求平均,即将损失均摊到每一个位置上,可得:
J(θ)=−1TlogL(θ)=−1T∑t=1T∑−m≤j≤m,j≠0logP(wt+j∣wt;θ)
J(\theta)=-\frac{1}{T}logL(\theta) = -\frac{1}{T}\sum_{t=1}^T\sum_{-m\le j \le m, j \ne 0} logP(w_{t+j}|w_t;\theta)
J(θ)=−T1logL(θ)=−T1t=1∑T−m≤j≤m,j=0∑logP(wt+j∣wt;θ)
那么问题转换成,如何求解P(wt+j∣wt;θ)P(w_{t+j}|w_t;\theta)P(wt+j∣wt;θ)?
对于每个单词www,令vwv_wvw表示一个中心词的向量表示,uwu_wuw表示一个上下文词的向量表示。那么对于一个中心词ccc和一个滑动窗口内的上下文单词ooo,
P(o∣c)=exp(uoTvc)∑w∈Vexp(uwTvc)
P(o|c) = \frac{exp(u_o^Tv_c)}{\sum_{w\in V} exp(u_w^Tv_c)}
P(o∣c)=∑w∈Vexp(uwTvc)exp(uoTvc)
其中VVV表示语料库中所有的词;向量的点积用于衡量向量间的相似度(物理含义为向量投影);expexpexp函数作为映射函数,将实数范围映射为正数,同时保证映射的大小关系;最后分母做归一化。
更准确说,这种求出概率的方式称为softmax\text{softmax}softmax,其把任意值xix_ixi映射为概率分布pip_ipi,一般写作:
softmax(xi)=exp(xi)∑j=1nexp(xj)=pi
\text{softmax}(x_i) = \frac{exp(x_i)}{\sum_{j=1}^{n}exp(x_j)} = p_i
softmax(xi)=∑j=1nexp(xj)exp(xi)=pi
称为softmax\text{softmax}softmax的原因为,其保证了最大的xmaxx_{max}xmax仍然最大且放大了其概率值;同时减小了其他值的概率值。
Word2vec的训练
我们使用梯度下降方法调整参数,使得目标函数不断下降到最小。θ\thetaθ表示所有的模型参数,ddd表示每个单词的向量维度长度,是一个超参数,在训练前手动指定。每个单词有两个向量,因为有一个作为uuu,一个作为vvv(一个作为中心词的表示,一个作为上下文单词的表示)。
通过计算概率公式,也就是上面的P(o∣c)P(o|c)P(o∣c)可以得出在已知中心词的情况下,各个词(语料库中所有词)作为上下文单词的概率,但是我们窗口大小是mmm(包括中心词在内),即找到最大的m−1m-1m−1的概率所对应的词向量,与输入已知的ground truth(也就是上下文单词对应的uuu)做交叉熵,作为单次迭代的损失,反向传播训练。
最后得到的各个单词的单词向量uuu,即为每个单词的embeddingembeddingembedding。
Word2vec的形式
Word2vec有两种形式,一种是输入中心词,预测周围上下文词,称为Skip-gram。另外一种是输入上下文词,预测中心词,称为Continue Bag Of Word(CBOW)。两种方法的核心思想是如出一辙的。





 探讨了词向量的概念,分布式语义表示及其在Word2Vec中的应用,包括Skip-gram与CBOW两种模型,以及如何通过上下文预测中心词或反之。
探讨了词向量的概念,分布式语义表示及其在Word2Vec中的应用,包括Skip-gram与CBOW两种模型,以及如何通过上下文预测中心词或反之。
















 2741
2741

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








