回归分析应用_多元线性回归模型中,已知多重判定系数为0.8,样本量为100,求调整的多重判定系数值-优快云博客

在统计学中，回归分析（regression analysis）指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。回归分析按照涉及的变量的多少，分为一元回归和多元回归分析；按照因变量的多少，可分为简单回归分析和多重回归分析；按照自变量和因变量之间的关系类型，可分为线性回归分析和非线性回归分析。

适用条件

在大数据分析中，回归分析是一种预测性的建模技术，它研究的是因变量（目标）和自变量（预测器）之间的关系。这种技术通常用于预测分析，时间序列模型以及发现变量之间的因果关系。

回归分析类型选择

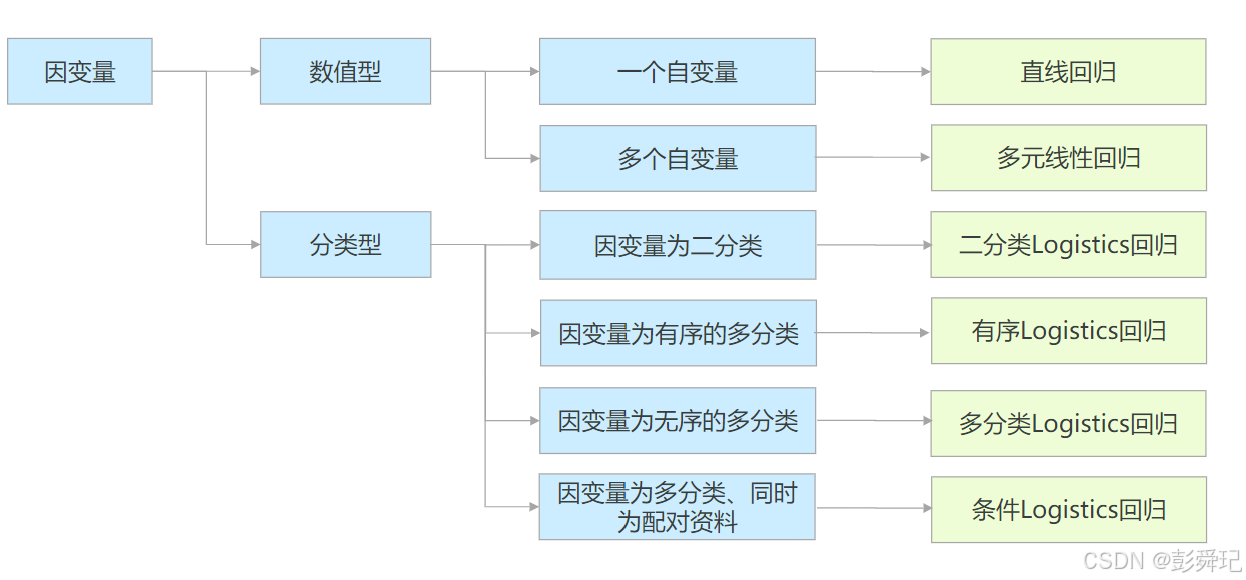
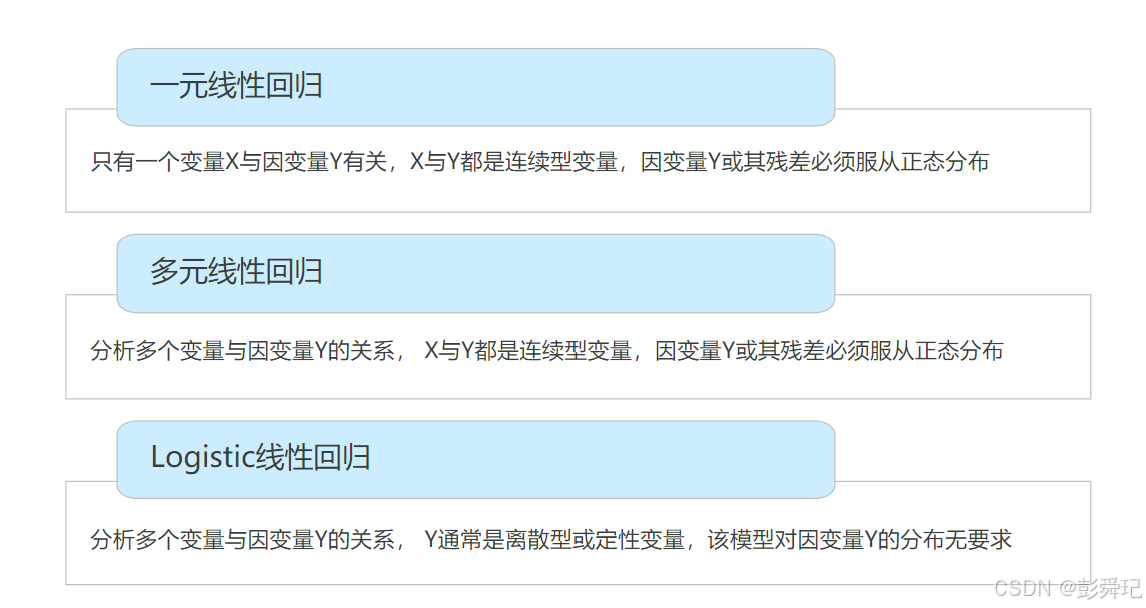
一元回归

一元线性回归

假定自变量 x 是一般变量，因变量 y 是随机变量。对于固定的 x 值，y 值有可能是不同的。假定 y 的均值是 x 的线性函数，并且波动是一致的。此外总假定 n 组数据的收集是独立进行的，在以下的检验及计算概率时还进一步假定 y 服从正态分布。在这些假定的基础上，建立如下一元线性回归模型：。其中

x 为自变量，y 为因变量。β_0 和 β_1 称为模型的参数，β_0 为截距，β_1 为回归系数，表明自变量对因变量的影响程度。误差项 ε 是随机变量，反映了除 x 和 y 之间的线性关系外的随机因素对 y 的影响，是不能由 x 和 y 之间的线性关系所解释的变异性。

一元非线性回归

实际问题中，变量之间常常不是直线。这时，通常是选配一条比较接近的曲线，通过变量替换把非线性方程加以线性化，然后按照线性回归的方法进行拟合。

常见的可转化一元线性回归的模型包括：

许多曲线都可以通过变换化为直线，于是可以按直线拟合的方法来处理。对变换后的数据进行线性回归分析，之后将得到的结果再代回原方程。因而，回归分析是对变换后的数据进行的，所得结果仅对变换后的数据来说是最佳拟合，当再变换回原数据坐标时，所得的回归曲线严格地说并不是最佳拟合，不过，其拟合程度通常是令人满意的。

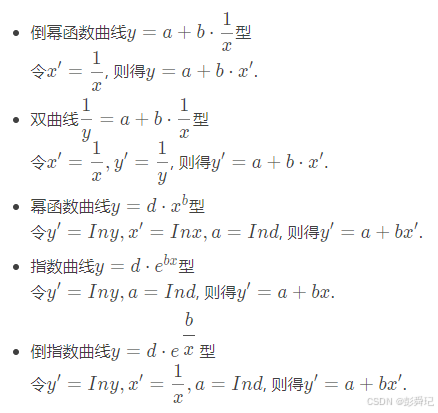
一元多项式回归

不是所有的一元非线性函数都能转换成一元线性方程，但任何复杂的一元连续函数都可用高阶多项式近似表示，因此对于那些较难直线化的一元函数，可用下式来拟合。

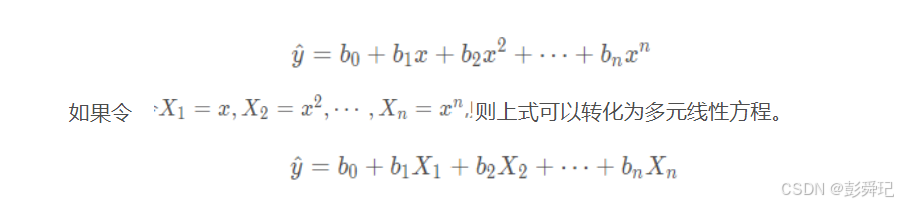
多元回归

多元线性回归

其表达式为:

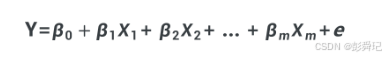
其中：βj（j = 1,2,...,n）表示在其他自变量保持不变时，x_j 增加或减少一个单元时 y 的平均变化量。

e表示去除m个自变量对Y影响后的随机误差。

多元多项式回归

一元二次多项式模型：y_i =β_0 +β_1 x_i +β_2 x_i² +ε_i，i = 1,2,...,n 是条抛物线，又被称为二项式回归函数。回归系数 β_1 为线性效应系数，β_2 为二次效应系数。

一元三次多项式模型：y_i =β_0 +β_1 x_i +β_2 x_i² +β_3 x_i³ +ε_i，i = 1,2,...,n。当自变量的幂次超过 3 时，回归系数解释变的困难，并且不稳定，因此不常用。

二元二次多项式模型：y_i =β_0 +β_1 x_i1 +β_2 x_2 +β_21 x_i²+β_22 x_i²+β_12 x_1 x_2 +ε_i。其中，β_12 x_i1 x_i 被称作交叉乘积项，表示了自变量 x_1 和 x_2 的交互作用，β_12 被称作交叉影响系数。

多项式回归可以转换成线性回归，但是要注意自变量和高次自变量之前有很强的相关性，需要考虑多重共线性的影响。

数据预处理

标准化（Standardization）：将数据转换为均值为 0，标准差为 1 的分布。标准化可以提高模型的性能和稳定性，特别是在使用梯度下降等优化算法时。

归一化（Normalization）：将数据转换为特定的范围，例如 [0, 1] 或 [-1, 1]。归一化可以避免不同变量之间的量纲差异对模型的影响。

模型选择与优化

变量选择：选择对因变量有重要影响的自变量，可以通过逐步回归、Lasso 回归、Ridge 回归等方法进行变量选择。

模型优化：调整模型的参数，以提高模型的性能。可以使用交叉验证等方法来选择最佳的模型参数。

应用场景

预测：根据已知的自变量值，预测因变量的值。

关系研究：研究自变量与因变量之间的关系，例如确定哪些因素对销售额有显著影响。

政策评估：评估政策变化对因变量的影响，例如税收政策对经济增长的影响。

一元线性回归模型实例

题目

对数据进行一元线性回归分析

内容

先要引入需要的库

#引入姿用的库
import math
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error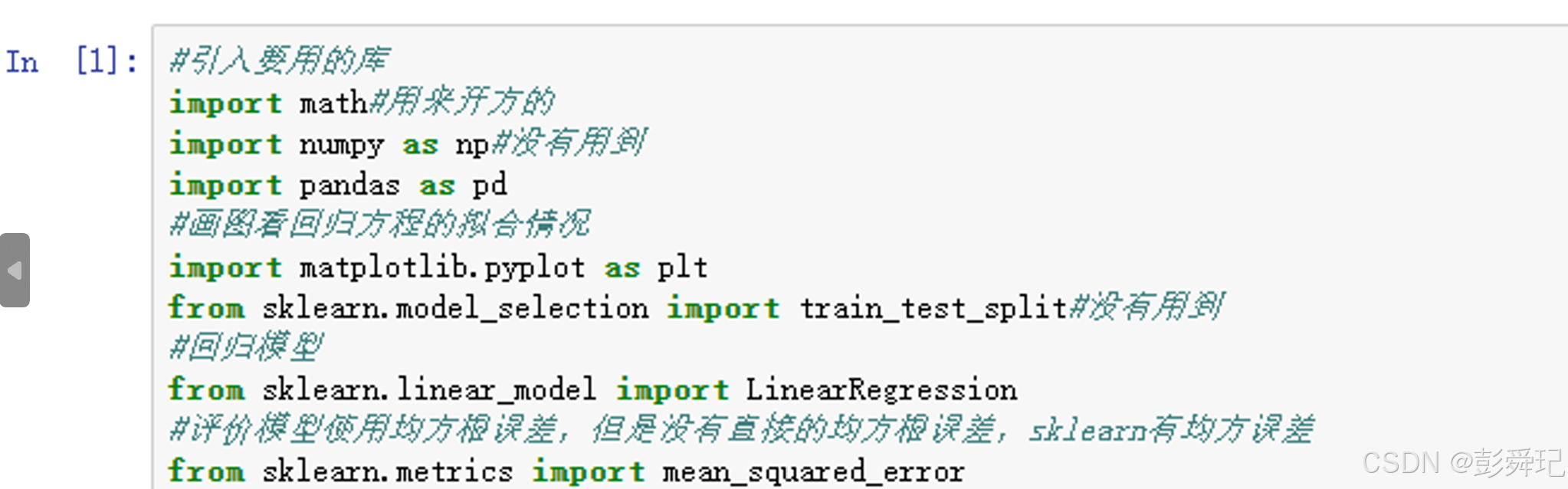

再导入的数据文件

data=pd.read_csv('C:/Users/adnin/esktop/ODS_PROV_GDP_TA_INF0.csv', encoding='gb2312')
data.head()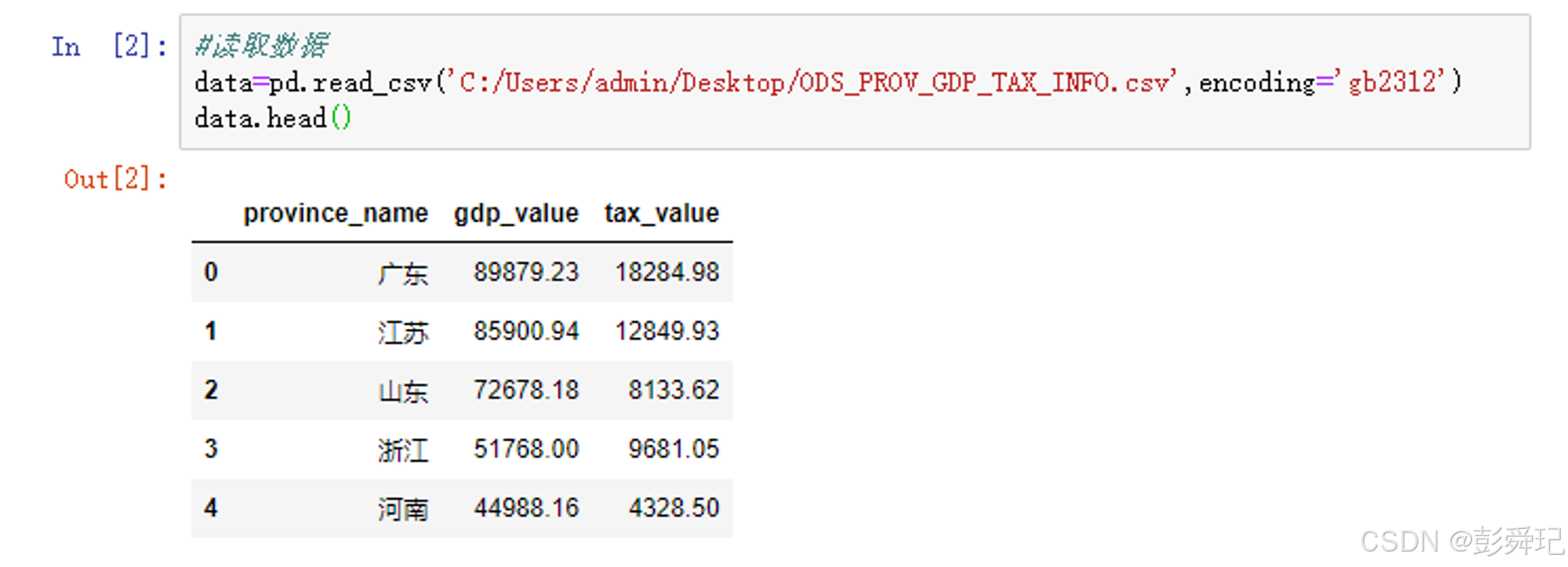

统计类型

describe() 方法用于生成描述性统计信息，它可以对数据框（DataFrame）或一系列（Series）对象进行操作。

data.describe()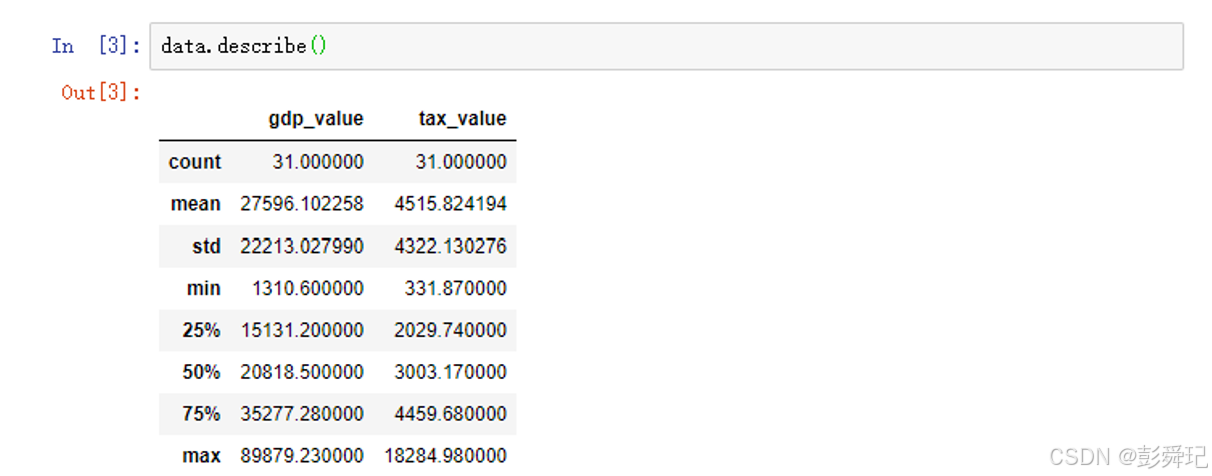

查看数据的基本信息

info()查看数据是否有缺失值

data.info()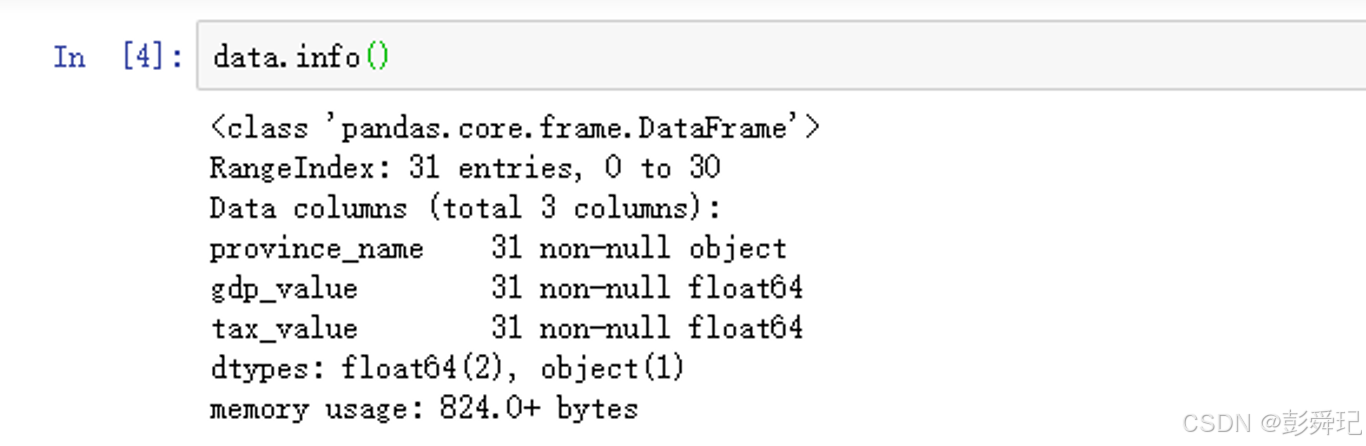

切割数据

# 切割x和y
y = data['tax_value'].values
x = data['gdp_value'].values

构建线性回归模型并拟合

model = LinearRegression()
model.fit(x, y)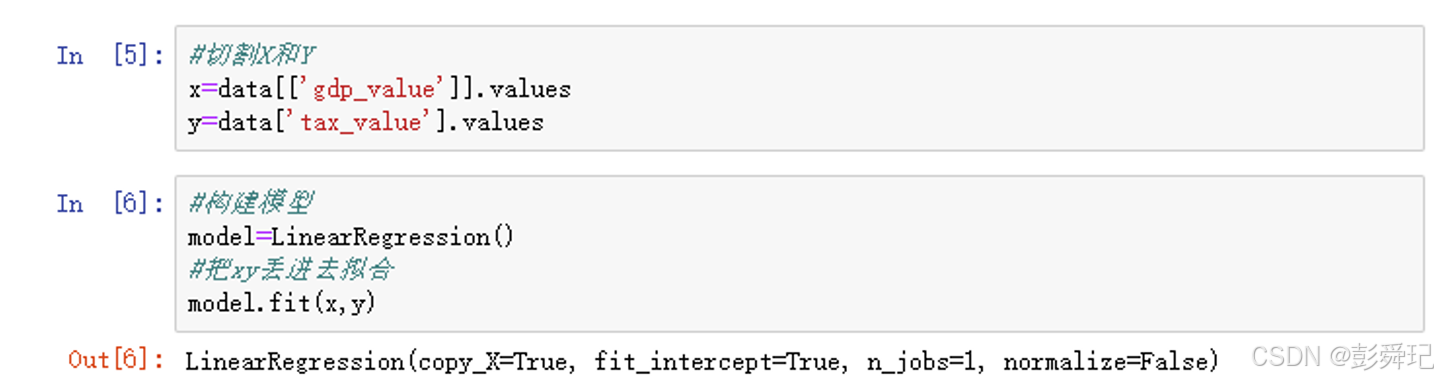

打印模型

# 打印模型的截距项和回归系数
print('模型的截距项(a)是:{}, 回归系数(b)是:{}'.format(model.intercept_, model.coef_))

计算均方根误差

# 计算均方根误差（RMSE）并打印
print('模型的RMSE值:{}'.format(math.sqrt(mean_squared_error(y, model.predict(x)))))

画图查看模型拟合

# 画图查看模型拟合情况
plt.plot(x, y, 'b.')
plt.plot(x, model.predict(x), 'r')
plt.xlabel('GDP')
plt.ylabel('tax')
plt.grid(True)
plt.show()

画图结果

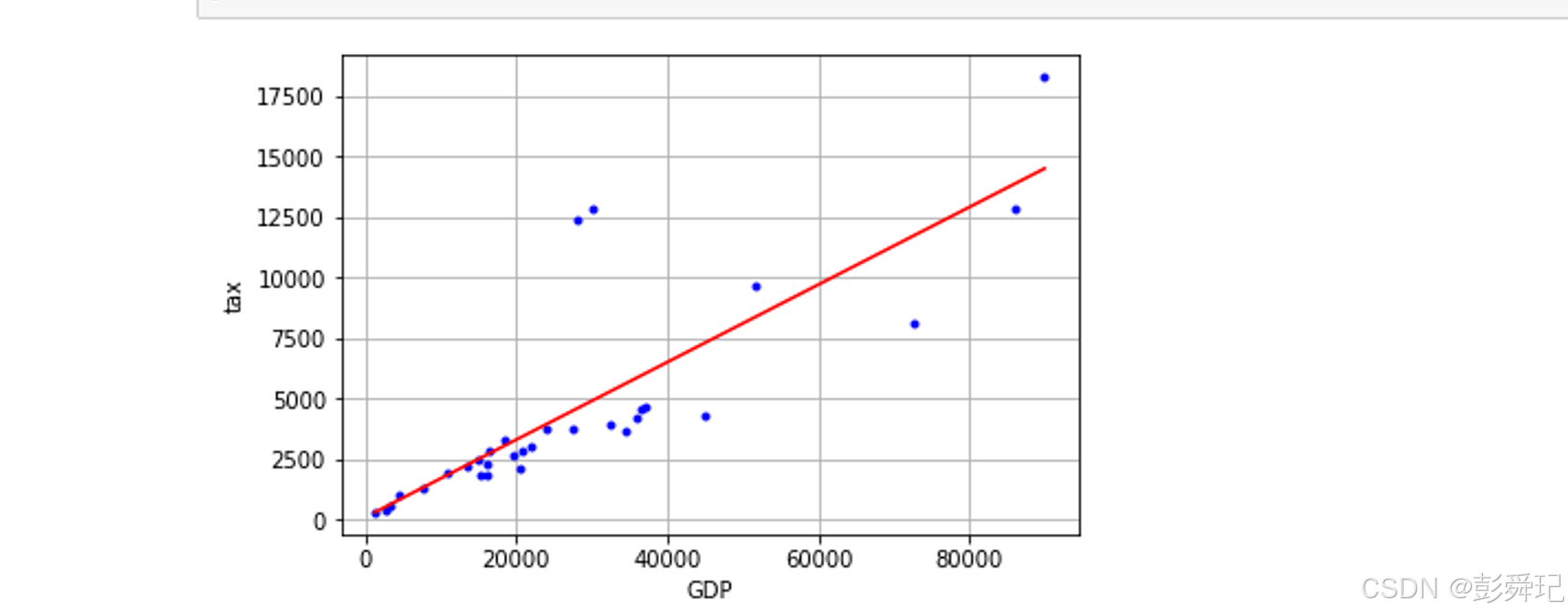
多元线性回归模型实例

题目

对数据进行多元线性回归分析

内容

先要引入需要的库

import math
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

再导入的数据文件

data = pd.read_csv('C:/Users/adnin/Desktop/ODS_PROV_GDP_TaX_CPI_EXPENDITURE_INFO.csv', encoding='gb2312')
data.head()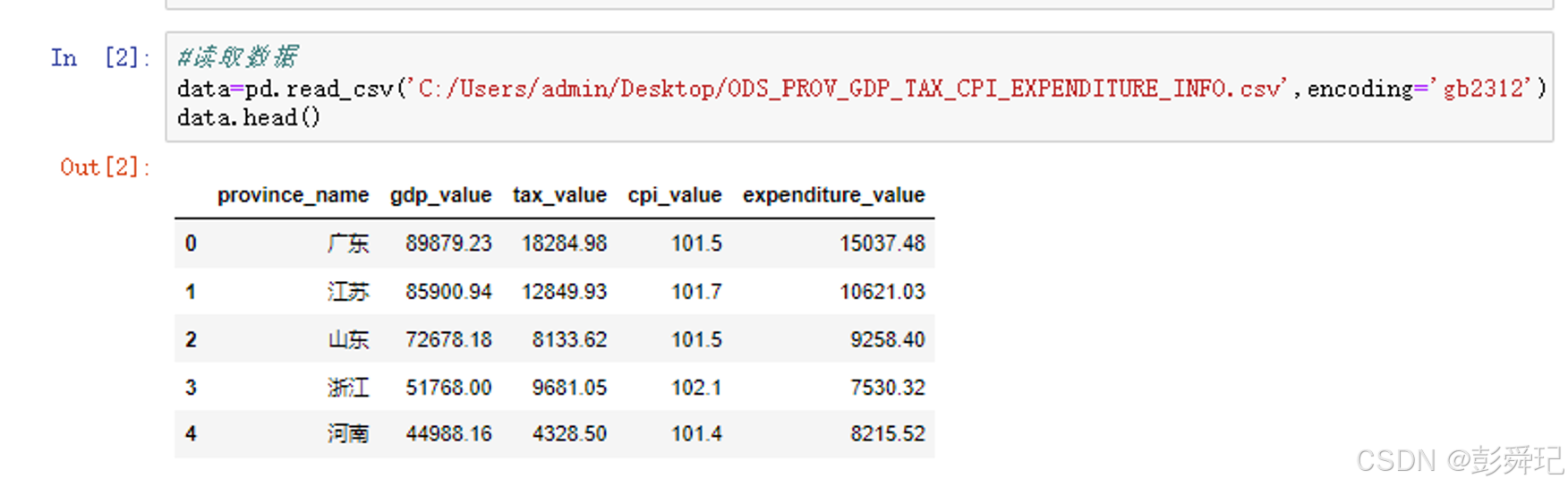

统计数据类型

data.describe()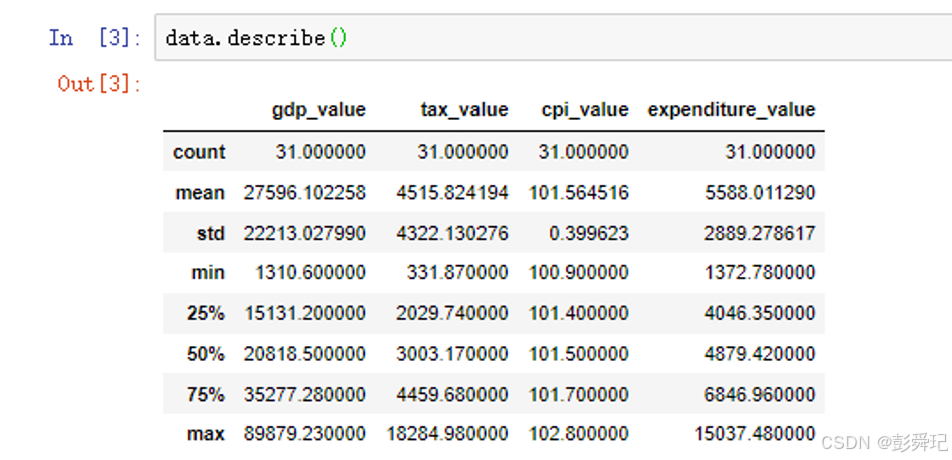

查看数据的基本信息

data.info()

定义 x 和 y

# 切割 X 和 y
X = data[['gdp_value','cpi_value','expenditure_value']].values
y = data['tax_value'].values

数据预处理

# 对 X 进行标准化
scaler = StandardScaler()
X_scaled = scaler.fit_transform(X)

构建模型

# 构建线性回归模型并拟合
model1 = LinearRegression()
model1.fit(X, y)

打印截距项和回归系数

# 打印未标准化的模型截距项和回归系数
print('未标准化的模型截距项是: {}, 回归系数是: {}'.format(model1.intercept_, model1.coef_))

打印均方根误差

# 计算并打印均方根误差
print('RMSE: {}'.format(math.sqrt(mean_squared_error(y, model1.predict(X)))))

打印 R 方值

# 计算并打印 R 方值
print('R方值: {}'.format(r2_score(y, model1.predict(X))))

预测

# 进行预测
print(model1.predict([[27202, 100.2, 4676.4]]))

总结

综上所述，通过不同类型的回归分析，我们可以深入了解经济变量之间的关系，建立有效的预测模型，并为实际问题提供决策支持。同时，在进行回归分析时，需要合理选择变量、进行适当的数据预处理，并选择合适的评估指标来确保模型的可靠性和有效性。