动态规划解0-1背包-优快云博客

本文链接：https://blog.youkuaiyun.com/penglei123456/article/details/86032363

动态规划适合求解最优问题，比如最大值最小值等。它可以显著的降低时间复杂度，提高代码的执行效率。

0-1 背包问题

在上篇总结中，用回溯算法解决了 0-1背包问题。但是，在求解的过程中，我们应该能想象的出，有些步骤是一直在重复执行。如果背包的总载重为 9 ，物品个数为 5 ，质量分别为 [2，2，4，6，3]。那么将这些数据带入回溯算法的代码中，执行阶段用递归树来表示：
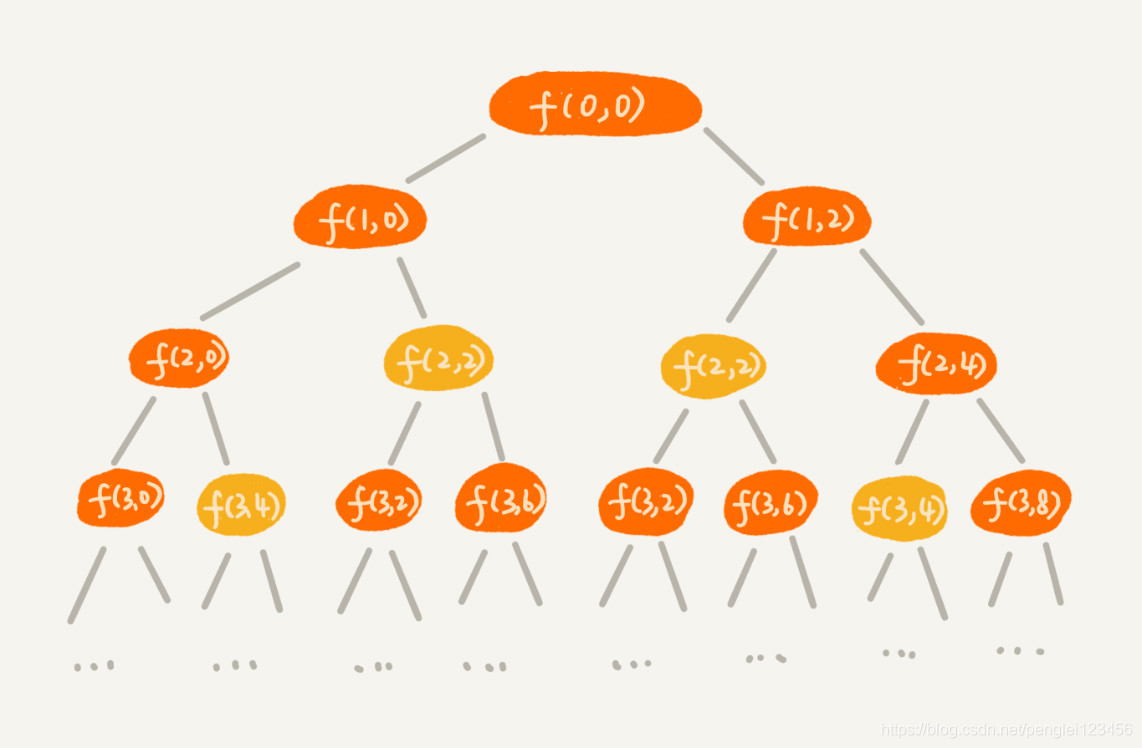
在这里插入图片描述

在上图中递归树中每个节点的状态，用 (i，cw) 来表示。i 表示要决策第几个物品是否放入背包，cw 代表当前背包的总质量。例如 (2，2) 代表第二个物品将决定是否放入背包，决策之前背包的总质量是 2。

通过上面的图例加说明，我们可以看出 f(2，2) 和 f(3，4) 都被重复计算了两次。为了减少重复计算的次数，我们可以把计算过的情况记录在案，当下次遇到相同的计算的时候，直接取值用就好。代码如下：

	// 存储背包中物品总重量的最大值
	public int maxW = Integer.MIN_VALUE; 

	private int[] weight = {2,2,4,6,3};  // 物品重量
	private int n = 5; // 物品个数
	private int w = 9; // 背包承受的最大重量
	private boolean[][] mem = new boolean[5][10]; // 备忘录，默认值 false
	
	/**
	 * 
	 * @param i  表示任务进行的阶段，考察到哪个物品了
	 * @param cw 表示当前已经装进去的物品的重量和
	 * @param items 数组存放每个物品的质量
	 */
	public void f(int i, int cw) {
		// cw==w 表示装满了 ;i==n 表示已经考察完所有的物品
		if (cw == w || i == n) { 
			if (cw > maxW){
				maxW = cw;			
			}
			return;
		}
		
		if (mem[i][cw]){
			return; // 重复状态
		}
		mem[i][cw] = true; // 记录 (i, cw) 这个状态
		
		//该物品不放入背包
		f(i + 1, cw);
		
		//该物品放入背包，物品放入背包的时候，需要判断当前物品总质量是否小于等于背包的承载重量
		if (cw + weight[i] <= w) {
			//放入该物品，进行下一个阶段
			f(i + 1, cw + weight[i]);
		}
	}

上面的过程理解之后，接下来总结动态规划如何实现上面的过程。

求解的过程分解成 n 个阶段，n 代表物品的数量。每个阶段，决定一个物品是否放入，决策之后，背包的重量会发生变化，这个变化的状态对应到递归树中就是不同的节点。

现在，我们把递归树中每一层中相同状态的节点合并，只留下不同状态的集合，并且在本次状态集合下去推导下一次的状态集合。由于我们值保存不相同的状态，并且总重量不能大于 w (w 代表总重量)，所以每层的状态集合最多有 w 个。(此处补充一下：前提是物品的质量都是整数，不可分割。)这样我们就避免了每一层的结果集成指数增长。

针对每一层的状态集，创建一个 states[n][w + 1] 二维数组来存储。n 代表层级，w + 1 代表结果集区间是从 0 到 w + 1。

对于放入第 0 个物品，质量为 2 ，对应数组中就是 states[0][0] = true，states[0][2] = true。states[0][0] 代表没有放入，states[0][2] 代表放入。以此类推，整个过程就是如下图所示：

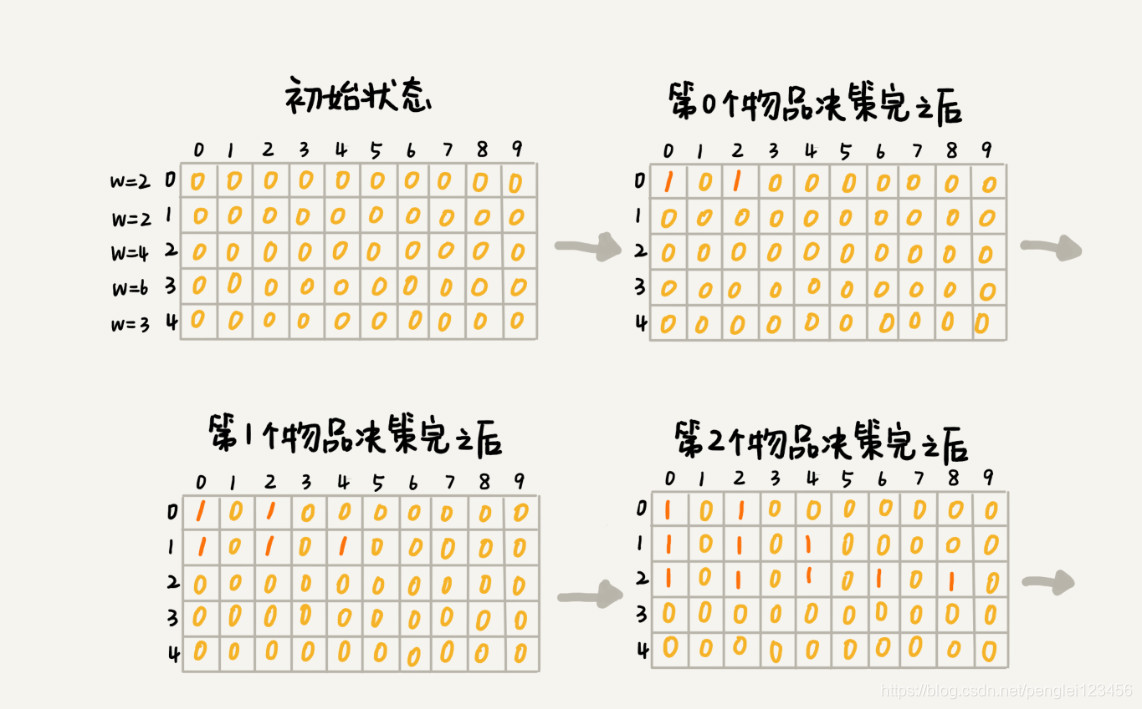
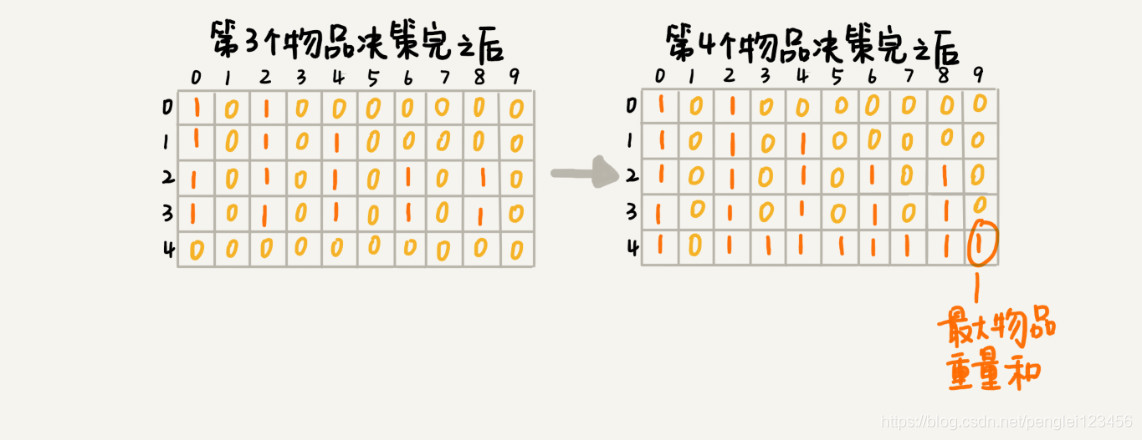
在这里插入图片描述

代码如下：

	// weight: 物品重量，n: 物品个数，w: 背包可承载重量
	public int knapsack(int[] weight, int n, int w) {
		boolean[][] states = new boolean[n][w + 1]; // 默认值 false
		// 第一个物品不放
		states[0][0] = true; 
		// 第一个物品放
		states[0][weight[0]] = true;
		// 遍历 n 个物品等于执行 n 个阶段
		for (int i = 1; i < n; ++i) { 
			// 以下两个 for 循环执行动态规划状态转移
			
			// 不把第  i 个物品放入背包
			for (int j = 0; j <= w; ++j) {
				//如果上一层有状态，直接转移到本层
				if (states[i - 1][j] == true){
					states[i][j] = states[i - 1][j];
				}					
			}
			// 把第 i 个物品放入背包
			// w - weight[i] 代表该物品放入之后，只有 j 以及 j 前面的不超重
			for (int j = 0; j <= w - weight[i]; ++j) {
				if (states[i - 1][j] == true){
					//叠加上一层的状态存起来
					states[i][j + weight[i]] = true;
				}
			}
		}
		for (int i = w; i >= 0; --i) { 
			// 输出最后一层结果
			if (states[n - 1][i] == true)
				return i;
		}
		return 0;
	}

上述代码中有详细的注释，足以看懂整个过程。

上面所举的例子以及代码的实现，就是一个动态规划算法的实现。将问题分阶段解决，每个阶段都有不同的结果集，我们合并相同的结果集，然后用该结果集去推到下一阶段的结果集，这就是一个动态规划的过程。

当然，上述代码虽然比起回溯算法提高了效率，但是却需要额外开辟一个二维数组，增加可空间的消耗。下面用代码实现一种用一维数组完成的动态规划：

	public static int knapsack2(int[] items, int n, int w) {
		boolean[] states = new boolean[w + 1]; // 默认值 false
		// 第一个物品不放入背包
		states[0] = true; 
		// 第一个物品不放入背包
		states[items[0]] = true;
		for (int i = 1; i < n; ++i) { // 动态规划
			// 把第 i 个物品放入背包
			// w - items[i] 代表该物品放入之后，只有 j 以及 j 前面的不超重
			for (int j = w - items[i]; j >= 0; --j) {
				if (states[j] == true){
					// 叠加上一层的状态存起来
					states[j + items[i]] = true;
				}
			}
		}
		for (int i = w; i >= 0; --i) { // 输出结果
			if (states[i] == true)
				return i;
		}
		return 0;
	}

上述代码之所以可以用一维数组实现，主要是省略了每一层中物品不放入背包的逻辑。如果不省略，进行了不放入背包的判断，其实只是把上一次的状态搬移到本层。但是这次搬移其实是无用功的，因为上一层已经满足的条件，搬移到这一整层，依旧是满足条件的。所以，有意义的操作就是对本层物品放入的判断。另外一个原因，因为是动态规划，我们都是用上一层的结果集推导下一层的结果集。也就是说，当本层的结果集推导出来后，上一层的结果集已经没有用处了。所以，我们才可以采用本层额结果集覆盖上层的结果集，最终完成动态规划。