53 给定一个整数数组，找到一个具有最大和的连续子数组，返回其最大和

点击此处返回总目录     【题目】   【方法一】 求和最大的一段nums[a]+...+nums[b]最大，即sum[b] - sum[a-1]最大。 我们先来求出sum数组。sum[i]为从前i项和。 原数组：[-2,  1,  -3,  4,  -1,  2,  1,  -5,  4] 累加和：[-2, -1,  -4,  0,  -1,  1,  2,  -3,  1] 现在的问题是，前面找一个数i，后面找一个数j，使得两数之差sum[j]-sum[i]最大。这就类似于121题，求股票的最大收益，前面找一个值买入，后面找一个值卖出，然后求最大收益。 不过这里有点不一样，就是如果都是正数，如3,2,4,8,1。最好的结果为8，不是8-2=6。所以，如果前面的数是正数，减去一个正数会变小，不如不减。只有前面是负数的时候，减去一个负数会变大。因此，可以设初试的min=0。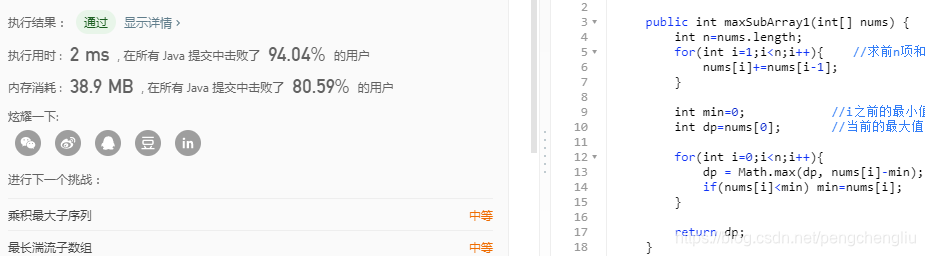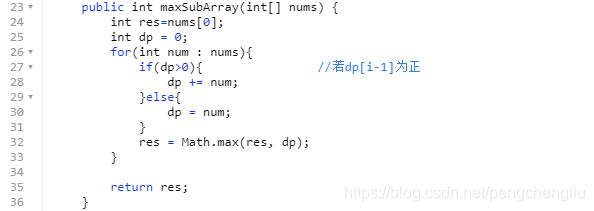   dp式子： 前i项的最大值 = max{前i-1项的最大值，sum[i]-min}   代码：   结果：       【方法二】 dp[i]表示以第i个元素为结尾的连续子数组的最大和。 以第i个元素为结尾的最大和 = max{只有自己一个元素nums[i]，以第i-1为结尾的最大和+nums[i]}。因此： if(dp[i-1]<0){      dp[i] = nums[i]; }else{      dp[i] = dp[i-1]+nums[i]; }   举例： 原数组：[-2,  1,  -3,  4,  -1,  2,  1,  -5,  4] dp[0]   ：[-2,                                          ]     //dp[0]=-2 dp[1]   ：[-2,  1                                      ]     //因为dp[0]=-2，所以以1结尾的最大的和，不如不加前面的负数。 dp[2]   ：[-2,  1,  -2                                ]     //dp[1]=1，所以dp[2] = 1+nums[2] dp[3]   ：[-2,  1,  -2,  4                           ] dp[4]   ：[-2,  1,  -2,  4,  3                      ] dp[5]   ：[-2,  1,  -2,  4,  3,  5                 ] dp[6]   ：[-2,  1,  -2,  4,  3,  5,  6            ] dp[7]   ：[-2,  1,  -2,  4,  3,  5,  6,  1       ] dp[8]   ：[-2,  1,  -2,  4,  3,  5,  6,  1,  5  ]   结果为dp[6]=6。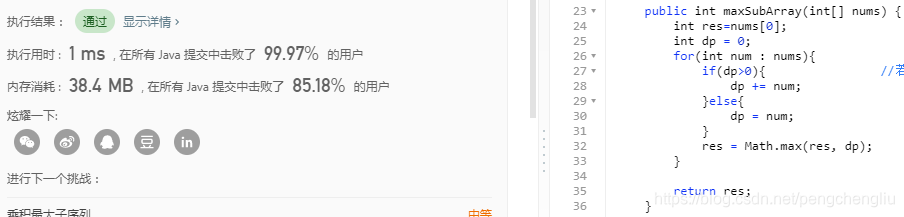   代码：   结果：