数据结构(11)-UnionFind(并查集)的实现与优化

今天来看看并查集的实现与优化～- ( ゜- ゜)つロ

1.1.什么是并查集

并查集这种数据结构的出现是为了解决一类被称为动态连通的问题：
所谓的动态连通问题是指在一组可能相互连接也可能相互没有连接的对象中，判断给定的两个对象是否联通的一类问题。

在并查集中需要对外提供两个方法，一是find(int x, int y)方法，用于查询x和y之间是否连通；二是union(int x, int y)方法，用于将x和y建立连通关系；

1.2.并查集的实现

底层基于一个parent数组，使用parent[i] = j，用来标识i的父节点为j,这样就可以实现元素之间的连通关系;在初始化并查集时，将每个节点的父节点都初始化为自己；

parent	0	1	2	3	4	5	6	7
element	0	1	2	3	4	5	6	7

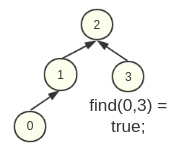
1. find(int x, int y)方法:
这个方法用于查询x和y是否连通，当x与y连通时返回true，反之返回false;实现的思路是判断两个元素的根节点是否为同一个即可判断：

/**
     * @auther: Arong
     * @description: 判断x和y是否属于同一集合
     * @param: [x, y]
     * @return: boolean
     * @date: 下午2:59 19-9-9
     */
    public boolean find(int x, int y) {
        return find(x) == find(y);
    }

    /**
     * @auther: Arong
     * @description: 查找child的根节点
     * @param: [child]
     * @return: int
     * @date: 下午3:06 19-9-9
     */
   private int find(int child) {
        if (child == parent[child]) return child;
        while (child != parent[child]) {
            child = parent[child];
        }
        return child;
    }

2. union(int x, int y)方法:
这个方法用于将x和y建立连通,即让他们拥有同一个根节点：

/**
    * @auther: Arong
    * @description: 将x和y连通
    * @param: [x, y]
    * @return: void
    * @date: 下午3:09 19-9-9
    */
   public void union(int x, int y) {
       //已是同一个祖先，已连通
       if (find(x) == find(y)) return;
       //让y的祖先成为x的父节点
       parent[find(x)] = find(y);
   }

1.3.优化1:高度优化

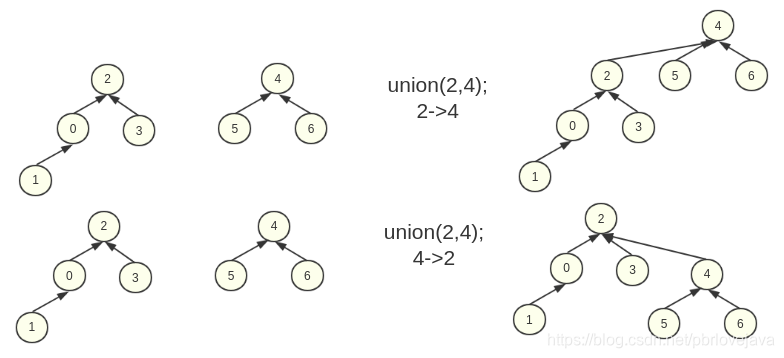
我们可以发现上述的实现中，find(int x)方法查找到根节点的时间和递归的深度有关，即和该节点到根节点的高度有关，当高度越低时，递归次数越少，搜索根节点的时间越短，但是按照我们的程序，可能出现这种情况:
即将2的根设置为4之后，整个连通集的高度增加了；但若设置4的根节点为2，效果都是一样的，但是连通集的高度仍为3；
所以此时可以维护一个rank数组，用来记录每个节点下树的高度；当进行union操作时，将高度小的那个节点设置为高度高的那个节点的子节点

/**
     * @auther: Arong
     * @description: 将x和y连通，增加rank判断
     * @param: [x, y]
     * @return: void
     * @date: 下午3:09 19-9-9
     */
    public void union(int x, int y) {
        //已是同一个祖先，已连通
        if (find(x) == find(y)) return;
        //高度大的节点为根节点
        if (rank[x] < rank[y]) {
            parent[x] = find(y);
            rank[y] += rank[x];
        } else if (rank[y] < rank[x]) {
            parent[y] = find(x);
            rank[x] += rank[y];
        } else {
            //两者高度相等
            parent[x] = find(y);
            rank[y] += 1;
        }
    }

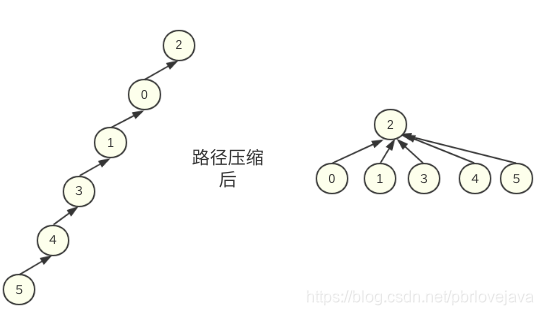
1.4.优化2:路径压缩

所谓的路径压缩，指的是在查询是否连通的过程中去将连通集压缩成２层，以便加速下次查询的时间：

private int find(int child) {
        if (child == parent[child]) return child;
        if (child != parent[child]) {
            //路径压缩
            parent[child] = find(parent[child]);
        }
        return parent[child];
    }

1.５.总体代码实现

/**
 * @Auther: ARong
 * @Date: 19-9-9 下午2:56
 **/
public class UnionFind_Rank {
    //parent数组，标识每个节点对应的父节点，当父节点=当前节点时则表明其已为根节点
    private int[] parent;
    //rank数组维护着每个节点的高度
    private int[] rank;

    public UnionFind_Rank(int capacity) {
        parent = new int[capacity];
        rank = new int[capacity];
        for (int i = 0; i < capacity; i++) {
            //每个节点的父节点都初始化为当前节点
            parent[i] = i;
            rank[i] = 1;
        }
    }
    /**
     * @auther: Arong
     * @description: 判断x和y是否属于同一集合
     * @param: [x, y]
     * @return: boolean
     * @date: 下午2:59 19-9-9
     */
    public boolean find(int x, int y) {
        return find(x) == find(y);
    }

    /**
     * @auther: Arong
     * @description: 查找child的根节点
     * @param: [child]
     * @return: int
     * @date: 下午3:06 19-9-9
     */
    private int find(int child) {
        if (child == parent[child]) return child;
        if (child != parent[child]) {
            //路径压缩
            parent[child] = find(parent[child]);
        }
        return parent[child];
    }

    /**
     * @auther: Arong
     * @description: 将x和y连通
     * @param: [x, y]
     * @return: void
     * @date: 下午3:09 19-9-9
     */
    public void union(int x, int y) {
        //已是同一个祖先，已连通
        if (find(x) == find(y)) return;
        //高度大的节点为根节点
        if (rank[x] < rank[y]) {
            parent[x] = find(y);
            rank[y] += rank[x];
        } else if (rank[y] < rank[x]) {
            parent[y] = find(x);
            rank[x] += rank[y];
        } else {
            //两者高度相等
            parent[x] = find(y);
            rank[y] += 1;
        }
    }

}