LeetCode(8)-回溯:组合排列问题

今天来总结下LeetCode上关于回溯的应用之排列组合相关的问题 - ( ゜- ゜)つロ

1.1 LeetCode 46.全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

一般的排列组合问题的本质都是枚举，对于枚举来说，最适合的算法就是回溯算法，我画了副图来理解这个过程：

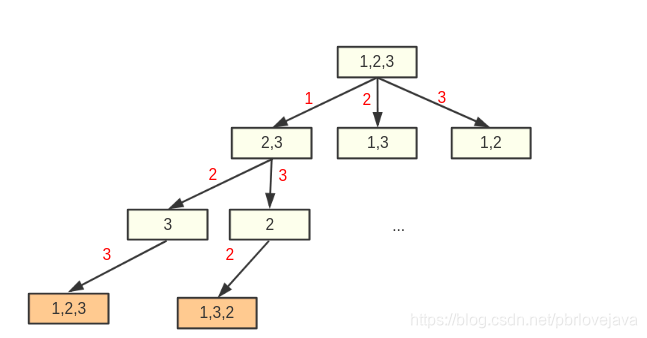
白色框框即为可以取值的数组，红色的数字是取出的数字，而黄色框框则为最后的结果；可以看到这是一个典型的树型结构解，而递归适合解对称类型的树型结构问题，例如二叉树问题，所以采用特殊的递归手段：回溯来解决这个问题：

private List<List<Integer>> res = new ArrayList<>();
    private boolean[] used;
    public List<List<Integer>> permute(int[] nums) {
        used = new boolean[nums.length];
        backTraceSearch(nums, 0, new LinkedList<Integer>());
        return res;
    }

    /**
     * @auther: Arong
     * @description: 回溯搜索
     * @param: [nums:含有所有元素的数组, count:当前结果中已有的元素个数, oneRes：存储当前结果]
     * @return: void
     */
    private void backTraceSearch(int[] nums, int count, LinkedList<Integer> oneRes) {
        //回溯终止条件
        if (count == nums.length) {
            res.add(new ArrayList<Integer>(oneRes));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            //当前结果中没有被使用到的元素才可取出
            if (!used[i]) {
                //已使用当前元素，标识为true，在下一次回溯搜索中不要使用该元素
                used[i] = true;
                //将当前结果添加到oneRes中，count + 1
                oneRes.addLast(nums[i]);
                //回溯搜索
                backTraceSearch(nums, count + 1, oneRes);
                //将状态变回原来的状况
                oneRes.removeLast();
                used[i] = false;
            }
        }
        return;
    }

1.2 LeetCode 47. 全排列 II

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/permutations-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

这个问题和46题是一样的思路，但是不能像之前那样全部枚举出来，因为数组中存在重复的元素，这时就需要用到剪枝优化技术：即在回溯搜索的过程中，剪去完全不可能成立的情况（路径），优化从而避免多余的搜索。
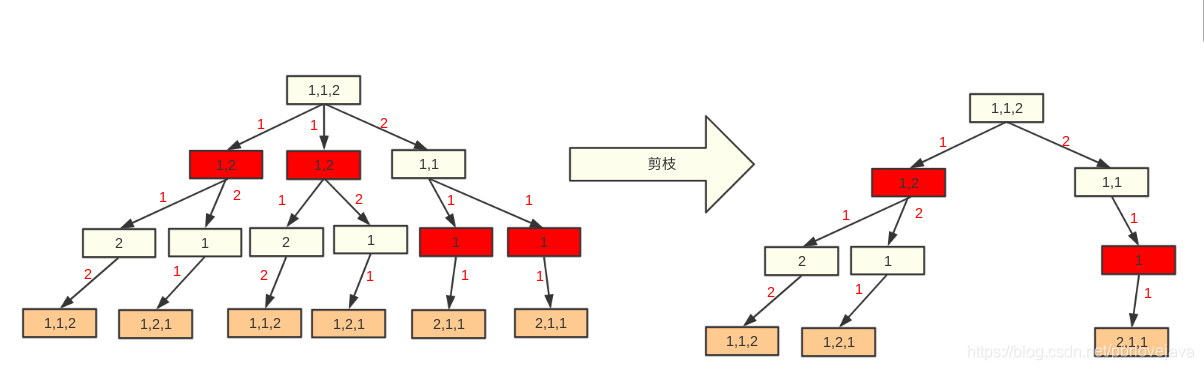
如下图，我们应该让红色方块在同一个层次中只存在一个，就能避免接下来多余的重复搜索了，那么如何进行剪枝呢？

从图中我们可以清晰地看到，当同一层次的节点取的值和上一个节点是一样的，譬如第二层的第一个节点取了1，第二个节点也取了1时，之后的搜索都是重复的，这就是剪枝的条件：nums[i] != nums[i - 1];

	private List<List<Integer>> res = new ArrayList<>();
    private boolean[] used = null;

    public List<List<Integer>> permuteUnique(int[] nums) {
        if (nums.length == 0) return res;
        used = new boolean[nums.length];
        //先对nums进行排序
        Arrays.sort(nums);
        serachWithPruning(nums, 0, new LinkedList<Integer>());
        return res;
    }

    /**
     * @auther: Arong
     * @description:  带有剪枝优化的回溯搜索
     * @param: [nums:含有所有元素的数组, count:当前结果中已有的元素个数, oneRes：存储当前结果]
     * @return: void
     */
    private void serachWithPruning(int[] nums, int count, LinkedList<Integer> oneRes) {
        //回溯终止条件
        if (count == nums.length) {
            res.add(new ArrayList<Integer>(oneRes));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
             //剪枝优化，nums[i - 1] == nums[i](i >= 1时 && !used[i - 1]表示的是上一节点取值和当前取值相同)
             if (i >= 1 && nums[i - 1] == nums[i] && !used[i - 1]) {
                    continue;
             }
            
             if (!used[i]) {
                used[i] = true;
                oneRes.addLast(nums[i]);
                //回溯搜索
                serachWithPruning(nums, count + 1, oneRes);
                //状态转变回来
                oneRes.removeLast();
                used[i] = false;
            }
        }
        return;
    }

1.3 LeetCode 77. 组合

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

输入: n = 4, k = 2
输出:
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/combinations
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

组合问题和排列问题不同的地方在于，用过的元素就不再使用,在方法参数中多传递一个start开始索引即可，每次将其+1

private List<List<Integer>> res = new ArrayList<>();
    private boolean[] used;

    public List<List<Integer>> combine(int n, int k) {
        if (n <= 0) return res;
        used = new boolean[n];
        backTraceSearch(n, k, 1, new LinkedList<Integer>());
        return res;
    }

    private void backTraceSearch(int n, int k, int start, LinkedList<Integer> oneRes) {
        //回溯终止条件
        if (oneRes.size() == k) {
            res.add(new ArrayList<Integer>(oneRes));
            return;
        }
        for (int i = start; i <= n; i++) {
            oneRes.offerLast(i);
            //回溯搜索
            backTraceSearch(n, k, i + 1, oneRes);
            //把状态变回来
            oneRes.removeLast();
        }
        return;
    }

未完持续…