二叉树的最近公共祖先

236. 二叉树的最近公共祖先 - 力扣（Leetcode）

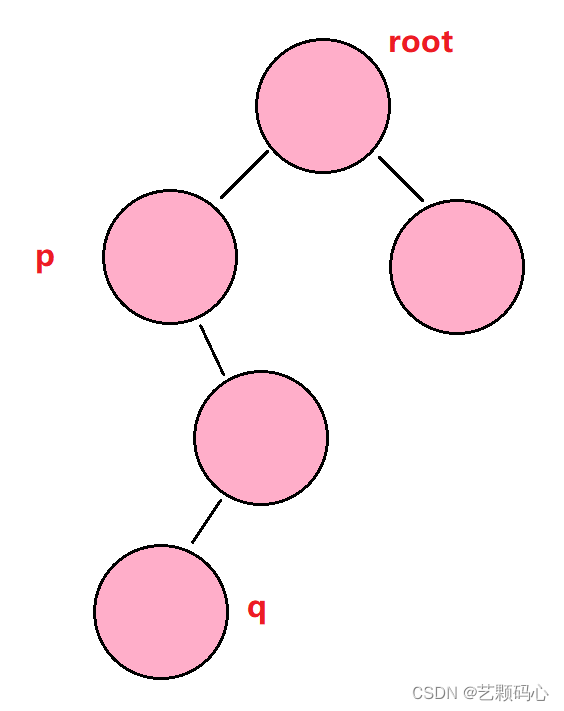
 解题思路 : 遍历方法,从root开始,判断root是不是p或者q,如果是的话,那就直接return root;

如果root不是那我们就去左子树去找 p q , 道理也是一样, 我们使用递归把root.left p  q 传进入.

再去递归右子树 , 传 root.right p  q .

左子树递归完会返回一个节点 或者 null ,  右子树递归完会返回一个节点 或者 null .

我们再去判断 如果左不为空,右也不为空,那就返回root,如果左为空,右不为空那就返回右子树递归返回的节点.如果左不为空,右为空那就返回左递归返回的节点.

具体代码实现 : 

方法一 : 

public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        if (root == p || q == root) {
            return root;
        }
        TreeNode left = lowestCommonAncestor(root.left,p,q);
        TreeNode right = lowestCommonAncestor(root.right,p,q);
        if (left != null && right != null) {
            return root;
        }
        if (left != null) {
            return left;
        }
        if (right != null) {
            return right;
        }
        return null;
    }

 方法二 : 

找到两个节点在root这棵树中的路径分别存在stack1 与 stack2. 如果stack1 的size() 比 stack2 的size()  大, 那就让stack1弹出栈顶元素直到与stack2的size相同,反之stack2大于stack1也弹出stack2中的元素直到与stack1的size相等.

重点在于如何找路径 :  

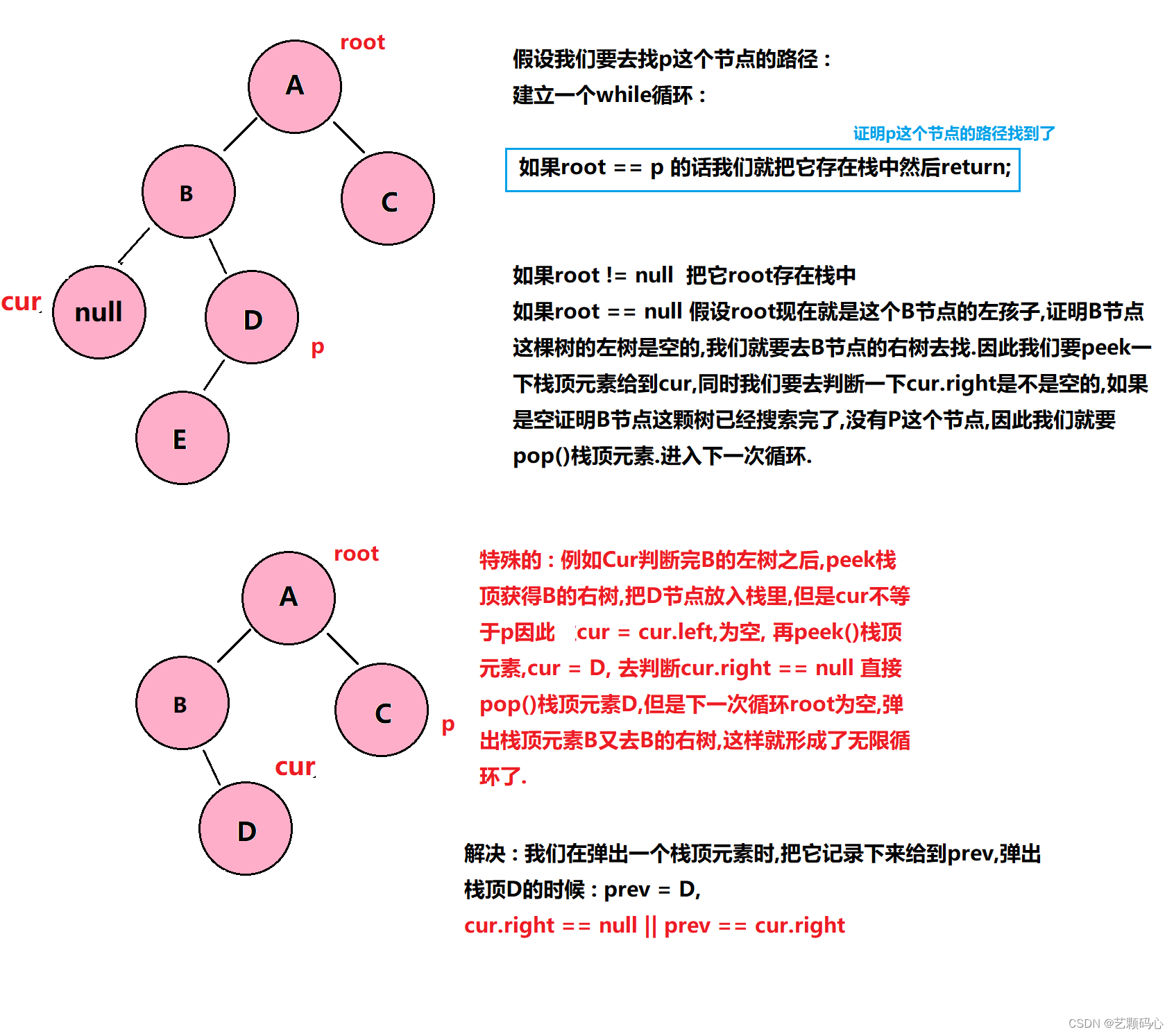
 代码实现 : 

使用while循环实现 : 

private boolean getPath (TreeNode root, TreeNode p, Stack<TreeNode> stack) {
        TreeNode prev = null;
        while (!stack.isEmpty() || root != null) {
            if (root == p) {
                stack.push(root);
                return true;
            }
            if (root != null) {
                stack.push(root);
                root = root.left;
            } else {
                TreeNode cur = stack.peek();
                if (cur.right == null || prev == cur.right) {
                    prev = stack.pop();
                } else {
                    root = cur.right;
                }
            }
        }
        return false;
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<TreeNode> stack2 = new Stack<>();
        //获得p的路径
        getPath(root,p,stack1);
        //获得q的路径
        getPath(root,q,stack2);
        int size1 = stack1.size();
        int size2 = stack2.size();
        int size = size1 - size2;
        if (size1 > size2) {
            while (size-- != 0) {
                stack1.pop();
            }
        } else {
            size = -size;
            while (size-- != 0) {
                stack2.pop();
            }
        }
        while (!stack1.empty()) {
            if (stack1.peek() == stack2.peek()) {
                return stack1.peek();
            } else {
                stack1.pop();
                stack2.pop();
            }
        }
        return null;
    }

使用递归实现 : 

private boolean getPath (TreeNode root, TreeNode p, Stack<TreeNode> stack) {
        if (root == null){
            return false;
        }
        stack.push(root);
        if (root == p) {
            return true;
        }
        boolean flag = getPath(root.left,p,stack);
        if (flag) {
            return true;
        }
        boolean right = getPath(root.right,p,stack);
        if (right) {
            return true;
        }
        stack.pop();
        return false;
    }
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        Stack<TreeNode> stack1 = new Stack<>();
        Stack<TreeNode> stack2 = new Stack<>();
        //获得p的路径
        getPath(root,p,stack1);
        //获得q的路径
        getPath(root,q,stack2);
        int size1 = stack1.size();
        int size2 = stack2.size();
        int size = size1 - size2;
        if (size1 > size2) {
            while (size-- != 0) {
                stack1.pop();
            }
        } else {
            size = -size;
            while (size-- != 0) {
                stack2.pop();
            }
        }
        while (!stack1.empty()) {
            if (stack1.peek() == stack2.peek()) {
                return stack1.peek();
            } else {
                stack1.pop();
                stack2.pop();
            }
        }
        return null;
    }

有问题可以私信我~~