一、线性变换的概念
当一个矩阵 AAA 乘一个向量 v\boldsymbol vv 时,它将 v\boldsymbol vv “变换” 成另一个向量 AvA\boldsymbol vAv. 输入 v\boldsymbol vv,输出 T(v)=AvT(\boldsymbol v)=A\boldsymbol vT(v)=Av. 变换 TTT 和函数类似:对于函数,输入数字 xxx,输出 f(x)f(x)f(x);对于变换,输入一个向量 v\boldsymbol vv,我们用矩阵左乘这个向量,输出 T(v)T(\boldsymbol v)T(v). 我们更深入的目标是所有向量 v\boldsymbol vv 的变换,当我们用矩阵 AAA 左乘每个向量 v\boldsymbol vv 时,我们是在变换整个空间 VVV.
先从矩阵 AAA 开始,它将 v\boldsymbol vv 变换成 AvA\boldsymbol vAv,将 w\boldsymbol ww 变换成 AwA\boldsymbol wAw,当 u=v+w\boldsymbol u=\boldsymbol v+\boldsymbol wu=v+w 时,我们得到 AuA\boldsymbol uAu 等于 Av+AwA\boldsymbol v+A\boldsymbol wAv+Aw. 矩阵乘法 T(v)=AvT(\boldsymbol v)=A\boldsymbol vT(v)=Av 给出了一个线性变换(linear transformation):
一个 变换 T 对于每个输入的向量 v 都对应一个输出 T(v). 如果对于所有的 v 和 w 都满足如下条件,则这个变换是线性的: (a)T(v+w)=T(v)+T(w)(b)对于任意的 c 都有: T(cv)=cT(v)一个\,\pmb{变换\,T}\,对于每个输入的向量\,\boldsymbol v\,都对应一个输出\,T(\boldsymbol v).\,\\如果对于所有的\,\boldsymbol v\,和\,\boldsymbol w\,都满足如下条件,则这个变换是\pmb{线性}的:\\\,\\\color{blue}(a)\kern 5ptT(\boldsymbol v+\boldsymbol w)=T(\boldsymbol v)+T(\boldsymbol w)\kern 15pt(b)\kern 5pt对于任意的\,c\,都有:\,T(c\boldsymbol v)=cT(\boldsymbol v)一个变换T对于每个输入的向量v都对应一个输出T(v).如果对于所有的v和w都满足如下条件,则这个变换是线性的:(a)T(v+w)=T(v)+T(w)(b)对于任意的c都有:T(cv)=cT(v)
由上述定义可知,如果输入 v=0\boldsymbol v=\boldsymbol 0v=0,则输出一定是 T(v)=0T(\boldsymbol v)=\boldsymbol 0T(v)=0,我们可以将条件(a)和(b)合并成一个条件:
线性变换T(cv+dw)=cT(v)+dT(w)\pmb{线性变换}\kern 30pt\color{blue}T(c\boldsymbol v+d\boldsymbol w)=cT(\boldsymbol v)+dT(\boldsymbol w)线性变换T(cv+dw)=cT(v)+dT(w)
我们可以验证矩阵的乘法是线性的:A(cv+dw)=cAv+dAwA(c\boldsymbol v+d\boldsymbol w)=cA\boldsymbol v+dA\boldsymbol wA(cv+dw)=cAv+dAw.
线性变换的限制很强。假设变换 TTT 是对任意向量加上一个非零向量 u0\boldsymbol u_0u0,则 T(v)=v+u0, T(w)=w+u0T(\boldsymbol v)=\boldsymbol v+\boldsymbol u_0,\,T(\boldsymbol w)=\boldsymbol w+\boldsymbol u_0T(v)=v+u0,T(w)=w+u0,这个就不算线性的,我们对 v+w\boldsymbol v+\boldsymbol wv+w 作变换 TTT 会得到 v+w+u0\boldsymbol v+\boldsymbol w+\boldsymbol u_0v+w+u0,它并不等于 T(v)+T(w)T(\boldsymbol v)+T(\boldsymbol w)T(v)+T(w):平移不是线性的v+w+u0不等于T(v)+T(w)=(v+u0)+(w+u0)\pmb{平移不是线性的}\kern 15pt\boldsymbol v+\boldsymbol w+\boldsymbol u_0\kern 5pt不等于\kern 5ptT(\boldsymbol v)+T(\boldsymbol w)=(\boldsymbol v+\boldsymbol u_0)+(\boldsymbol w+\boldsymbol u_0)平移不是线性的v+w+u0不等于T(v)+T(w)=(v+u0)+(w+u0)只有当 u0=0\boldsymbol u_0=\boldsymbol 0u0=0 时才是线性的,此时这个变换简化为 T(v)=vT(\boldsymbol v)=\boldsymbol vT(v)=v,这个是恒等变换(identity transformation,没有任何变换,就如单位矩阵左乘向量一样)。这个当然是线性的,这种情况输入空间 V\pmb{\textrm V}V 和输出空间 W\textrm{\pmb W}W 是完全一样的。
“线性 + 平移(linear-plus-shift)” 变换 T(v)=Av+u0T(\boldsymbol v)=A\boldsymbol v+\boldsymbol u_0T(v)=Av+u0 称为 “仿射的(affine)”,尽管此时 TTT 不是线性的,但是直线变换后仍为直线。移动计算机图形时,就可以使用仿射变换。
【例1】选择一个固定的向量 a=(1,3,4)\boldsymbol a=(1,3,4)a=(1,3,4),令 T(v)T(\boldsymbol v)T(v) 是点积 a⋅v\boldsymbol a\cdot\boldsymbol va⋅v:
输入是 v=(v1,v2,v3),输出是 T(v)=a⋅v=v1+3v2+4v3\boxed{输入是\,\boldsymbol v=(v_1,v_2,v_3),\kern 20pt输出是\,T(\boldsymbol v)=\boldsymbol a\cdot\boldsymbol v=v_1+3v_2+4v_3}输入是v=(v1,v2,v3),输出是T(v)=a⋅v=v1+3v2+4v3点积是线性的。输入 v\boldsymbol vv 来自于三维空间,所以 V=R3\textrm{\pmb V}=\textrm{\pmb{R}}^3V=R3. 输出只是数字,所以输出空间是 W=R1\textrm{\pmb W}=\textrm{\pmb R}^1W=R1. 这个就相当于用行矩阵 A=[134]A=\begin{bmatrix}1&3&4\end{bmatrix}A=[134] 左乘 v\boldsymbol vv,即 T(v)=AvT(\boldsymbol v)=A\boldsymbol vT(v)=Av.
现在我们能够很好的判断哪些变换是线性的了,如果输出包含平方、乘积或长度,v12,v1v2v_1^2,v_1v_2v12,v1v2 或 ∣∣v∣∣||\boldsymbol v||∣∣v∣∣,则 TTT 就不是线性的。
【例2】长度 T(v)=∣∣v∣∣T(\boldsymbol v)=||\boldsymbol v||T(v)=∣∣v∣∣ 不是线性的。线性条件(a)要求 ∣∣v+w∣∣=∣∣v∣∣+∣∣w∣∣||\boldsymbol v+\boldsymbol w||=||\boldsymbol v||+||\boldsymbol w||∣∣v+w∣∣=∣∣v∣∣+∣∣w∣∣,条件(b)要求 ∣∣cv∣∣=c∣∣v∣∣||c\boldsymbol v||=c||\boldsymbol v||∣∣cv∣∣=c∣∣v∣∣. 这两个条件均不满足!
条件(a)不成立:三角形的边满足三角不等式 ∣∣v+w∣∣≤∣∣v∣∣+∣∣w∣∣||\boldsymbol v+\boldsymbol w||\le||\boldsymbol v||+||\boldsymbol w||∣∣v+w∣∣≤∣∣v∣∣+∣∣w∣∣.
条件(b)不成立:长度 ∣∣−v∣∣||-\boldsymbol v||∣∣−v∣∣ 是 ∣∣v∣∣||\boldsymbol v||∣∣v∣∣ 而不是 −∣∣v∣∣-||\boldsymbol v||−∣∣v∣∣. 对于负数 ccc,线性不成立。
【例3】(旋转)TTT 是将每个向量逆时针旋转 30°30°30° 的变换,TTT 的 “定义域(domain)” 是 xyxyxy 平面(所有的输入向量 v\boldsymbol vv),TTT 的 “值域(range)” 也是 xyxyxy 平面(所有旋转了的向量 T(v)T(\boldsymbol v)T(v))。我们不适用矩阵来描述就是:平面逆时针旋转 30°30°30°.
旋转变换是线性的吗?答案是肯定的。我们可以将两个向量旋转后相加,旋转后的向量之和 T(v)+T(w)T(\boldsymbol v)+T(\boldsymbol w)T(v)+T(w) 等于向量和的旋转 T(v+w)T(\boldsymbol v+\boldsymbol w)T(v+w). 在这个线性变换中,整个平面一起旋转。
二、线到线、三角形到三角形、基决定一切
Figure 8.1 展示了输入空间中从 v\boldsymbol vv 到 w\boldsymbol ww 的直线,也展示了输出空间中从 T(v)T(\boldsymbol v)T(v) 到 T(w)T(\boldsymbol w)T(w) 的直线。线性告诉我们:输入直线上的每一个点都映射到输出直线上;进一步地是:等间距的点映射为等间距的点。中点 u=12v+12w\boldsymbol u=\displaystyle\frac{1}{2}\boldsymbol v+\frac{1}{2}\boldsymbol wu=21v+21w 映射为中点 T(u)=12T(v)+12T(w)T(\boldsymbol u)=\displaystyle\frac{1}{2}T(\boldsymbol v)+\frac{1}{2}T(\boldsymbol w)T(u)=21T(v)+21T(w).
另一个图上升一个维度,现在我们有三个顶点 v1,v2,v3\boldsymbol v_1,\boldsymbol v_2,\boldsymbol v_3v1,v2,v3,这些输入有三个输出 T(v1),T(v2),T(v3)T(\boldsymbol v_1),T(\boldsymbol v_2),T(\boldsymbol v_3)T(v1),T(v2),T(v3),输入三角形映射为输出三角形,等间距的点仍然保持等间距(沿着边的和不在边上的都是如此),重心 u=13(v1+v2+v3)\boldsymbol u=\displaystyle\frac{1}{3}(\boldsymbol v_1+\boldsymbol v_2+\boldsymbol v_3)u=31(v1+v2+v3) 映射为重心 T(u)=13(T(v1)+T(v2)+T(v3))T(\boldsymbol u)=\displaystyle\frac{1}{3}(T(\boldsymbol v_1)+T(\boldsymbol v_2)+T(\boldsymbol v_3))T(u)=31(T(v1)+T(v2)+T(v3)).

线性性质可以扩展到三个向量或 n 个向量的组合:\color{blue}线性性质可以扩展到三个向量或\,n\,个向量的组合:线性性质可以扩展到三个向量或n个向量的组合:
线性的u=c1v1+c2v2+⋯+cnvn一定是变换为T(u)=c1T(v1)+c2T(v2)+⋯+cnT(vn)(8.1.1)\begin{array}{c}\pmb{线性的}\kern 15pt{\color{blue}\boldsymbol u=c_1\boldsymbol v_1+c_2\boldsymbol v_2+\cdots+c_n\boldsymbol v_n}\kern 15pt\pmb{一定是变换为}\\\\{\color{blue}T(\boldsymbol u)=c_1T(\boldsymbol v_1)+c_2T(\boldsymbol v_2)+\cdots+c_nT(\boldsymbol v_n)}\end{array}\kern 20pt(8.1.1)线性的u=c1v1+c2v2+⋯+cnvn一定是变换为T(u)=c1T(v1)+c2T(v2)+⋯+cnT(vn)(8.1.1)
由 222 个向量的性质得到推出 333 个向量情形的证明:T(cu+dv+ew)=T(cu)+dT(dv+ew)T(c\boldsymbol u+d\boldsymbol v+e\boldsymbol w)=T(c\boldsymbol u)+dT(d\boldsymbol v+e\boldsymbol w)T(cu+dv+ew)=T(cu)+dT(dv+ew),然后对右边的这些项继续应用线性性质,可以得到 cT(u)+dT(v)+eT(w)cT(\boldsymbol u)+dT(\boldsymbol v)+eT(\boldsymbol w)cT(u)+dT(v)+eT(w).
nnn 个向量的规则(8.1.1)给出线性变换最重要的性质:`
假设知道了一组基 v1,v2,⋯ ,v3\boldsymbol v_1,\boldsymbol v_2,\cdots,\boldsymbol v_3v1,v2,⋯,v3 的全部变换 T(v)T(\boldsymbol v)T(v),那么就知道了这个空间中任意向量 u\boldsymbol uu 的变换 T(u)T(\boldsymbol u)T(u).
理由是:空间中的任意向量 u\boldsymbol uu 均是基向量 vj\boldsymbol v_jvj 的线性组合,由线性性质可知,T(u)T(\boldsymbol u)T(u) 是输出 T(vj)T(\boldsymbol v_j)T(vj) 同样系数的线性组合。
【例4】变换 TTT 是求输入的导数:T(u)=dudxT(u)=\displaystyle\frac{\textrm du}{\textrm dx}T(u)=dxdu. 如何求 u=6−4x+3x2u=6-4x+3x^2u=6−4x+3x2 的导数?我们先从 1,x1,x1,x 和 x2x^2x2 的导数开始,这些就是基向量,它们的导数分别是 0,10,10,1 和 2x2x2x,那么可以使用线性性质求基向量任意线性组合的导数:dudx=6(1 的导数)−4(x 的导数)+3(x2 的导数)=−4+6x\frac{\textrm du}{\textrm dx}=6(1\,的导数)-4(x\,的导数)+3(x^2\,的导数)=-4+6xdxdu=6(1的导数)−4(x的导数)+3(x2的导数)=−4+6x微积分的内容都是基于线性性质的!微积分基础是先求出基本初等函数的导数,如 xn,sinx,cosxx^n,\sin x,\cos xxn,sinx,cosx 和 exe^xex,然后再对它们所有的组合使用线性性质。
微积分中唯一特殊的法则是链式法则(chain rule),链式法则给出了复合函数 f(g(x))f(g(x))f(g(x)) 的导数。
T(u)=dudxT(u)=\displaystyle\frac{\textrm du}{\textrm dx}T(u)=dxdu 的零空间:要得到零空间我们需要求解 T(u)=0T(u)=0T(u)=0. 当且仅当 uuu 是一个常数函数时其导数为零。所以零空间是一维的,它是函数空间中的一条线 —— 包含特解 u=1u=1u=1 所有的倍数。
T(u)=dudxT(u)=\displaystyle\frac{\textrm du}{\textrm dx}T(u)=dxdu 的列空间:该例中输入空间包含所有的二次函数 a+bx+cx2a+bx+cx^2a+bx+cx2,输出空间(列空间)是所有的线性函数 b+2cxb+2cxb+2cx. 注意计数定理 r+(n−r)=n\pmb{r+(n-r)=n}r+(n−r)=n 仍然成立。维数(列空间)+维数(零空间)=2+1=3=维数(输入空间)维数(\pmb{列空间})+维数(\pmb{零空间})=\pmb{2+1=3}=维数(\pmb{输入空间})维数(列空间)+维数(零空间)=2+1=3=维数(输入空间)求导 ddx\displaystyle\frac{\textrm d}{\textrm dx}dxd 对应的矩阵是什么?对于线性变换 T=ddxT=\displaystyle\frac{\textrm d}{\textrm dx}T=dxd,我们知道 TTT 对基函数的作用:v1,v2,v3=1,x,x2dv1dx=0dv2dx=1=v1dv3dx=2x=2v2(8.1.2)\boldsymbol v_1,\boldsymbol v_2,\boldsymbol v_3=\pmb{1,x,x^2}\kern 20pt\frac{\textrm d\boldsymbol v_1}{\textrm dx}=\boldsymbol 0\kern 20pt\frac{\textrm d\boldsymbol v_2}{\textrm dx}=1=\boldsymbol v_1\kern 20pt\frac{\textrm d\boldsymbol v_3}{\textrm dx}=2x=\pmb{2 v_2}\kern 18pt(8.1.2)v1,v2,v3=1,x,x2dxdv1=0dxdv2=1=v1dxdv3=2x=2v2(8.1.2)三维的输入空间 V\pmb{\textrm V}V(二次函数)变换到二维的输出空间 W\textrm{\pmb W}W(线性函数)。如果将 v1,v2,v3\boldsymbol v_1,\boldsymbol v_2,\boldsymbol v_3v1,v2,v3 当做向量,就可以得到变换矩阵A=[010002]是求导变换 T=ddx 的变换矩阵(8.1.3)\boxed{\pmb A=\begin{bmatrix}0&\pmb1&0\\0&0&\pmb2\end{bmatrix}是求导变换\,T=\frac{\textrm d}{\textrm dx}\,的变换矩阵}\kern 25pt(8.1.3)A=[001002]是求导变换T=dxd的变换矩阵(8.1.3)线性变换 dudx\displaystyle\frac{\textrm du}{\textrm dx}dxdu 可以完美的由矩阵的乘法 AuA\boldsymbol uAu 来解释。输入 ua+bx+cx2乘积 Au=[010002][abc]=[b2c]输出 dudx=b+2cx\begin{array}{l}\pmb{输入}\,\boldsymbol u\\a+bx+cx^2\end{array}\begin{array}{c}\pmb{乘积}\,A\boldsymbol u=\begin{bmatrix}0&1&0\\0&0&2\end{bmatrix}\begin{bmatrix}a\\b\\c\end{bmatrix}=\begin{bmatrix}b\\2c\end{bmatrix}&\pmb{输出\,\displaystyle\frac{\textrm du}{\textrm dx}}=b+2cx\end{array}输入ua+bx+cx2乘积Au=[001002]abc=[b2c]输出dxdu=b+2cxTTT 和 AAA 之间的联系(我们可以对每个线性变换都确定一个变换矩阵)依赖于输入基 1,x,x21,x,x^21,x,x2 和输出基 1,x1,x1,x 的选取。
下面看积分,它们给出导数的伪逆 T+T^+T+ ! 这里不能写成 T−1T^{-1}T−1,那么也不能说 “ TTT 的逆 ”,因为所有常数函数的导数都是 000,这是多对一的情况。
【例5】积分 T+T^+T+ 也是线性的:∫0x(D+Ex) dx=Dx+12Ex2\int_0^x(D+Ex)\,\textrm dx=Dx+\displaystyle\frac{1}{2}Ex^2∫0x(D+Ex)dx=Dx+21Ex2.
现在输入基是 1,x1,x1,x,输出基是 1,x,x21,x,x^21,x,x2,T+T^+T+ 对应的矩阵 A+A^+A+ 是 3×23\times23×2 的:输入 vD+Ex乘积 A+v=[001001/2][DE]=[0D12E]输出 v 的积分T+(v)=Dx+12Ex2\begin{array}{l}\pmb{输入\,v}\\D+Ex\end{array}\kern 10pt\pmb{乘积}\,A^+\boldsymbol v=\begin{bmatrix}0&0\\1&0\\0&1/2\end{bmatrix}\begin{bmatrix}D\\E\end{bmatrix}=\begin{bmatrix}\pmb0\\\pmb D\\\pmb{\displaystyle\frac{1}{2}E}\end{bmatrix}\kern 5pt\begin{array}{l}\pmb{输出\,v\,的积分}\\T^+(\boldsymbol v)=Dx+\displaystyle\frac{1}{2}Ex^2\end{array}输入vD+Ex乘积A+v=010001/2[DE]=0D21E输出v的积分T+(v)=Dx+21Ex2微积分基本定理指出:积分是微分的(伪)逆。从线性代数来看,矩阵 A+A^+A+ 是矩阵 AAA 的伪逆:A+A=[001001/2][010002]=[000010001]AA+=[1001](8.1.4)A^+A=\begin{bmatrix}0&0\\1&0\\0&1/2\end{bmatrix}\begin{bmatrix}0&1&0\\0&0&2\end{bmatrix}=\begin{bmatrix}\pmb0&0&0\\0&\pmb1&0\\0&0&\pmb1\end{bmatrix}\kern 15ptAA^+=\begin{bmatrix}\pmb1&0\\0&\pmb1\end{bmatrix}\kern 19pt(8.1.4)A+A=010001/2[001002]=000010001AA+=[1001](8.1.4)常数函数的导数是零,零在 A+AA^+AA+A 的对角线上。如果 T=ddxT=\displaystyle\frac{\textrm d}{\textrm dx}T=dxd 没有一维的零空间,则微积分就不是微积分了(不再完整)。
三、变换的例子(大部分是线性的)
【例6】将任意三维向量投影到水平面 z=1z=1z=1 上:向量 v=(x,y,z)\boldsymbol v=(x,y,z)v=(x,y,z) 变换为 T(v)=(x,y,1)T(\boldsymbol v)=(x,y,1)T(v)=(x,y,1). 这个向量不是线性的。为什么呢?因为 v=0\boldsymbol v=\boldsymbol 0v=0 甚至没有变换为 T(v)=0T(\boldsymbol v)=\boldsymbol 0T(v)=0.
【例7】假设 AAA 是一个可逆矩阵,则有 T(v+w)=Av+Aw=T(v)+T(w)T(\boldsymbol v+\boldsymbol w)=A\boldsymbol v+A\boldsymbol w=T(\boldsymbol v)+T(\boldsymbol w)T(v+w)=Av+Aw=T(v)+T(w). 另一个线性变换是用 A−1A^{-1}A−1 左乘,这个给出了逆变换(inverse transformation)T−1T^{-1}T−1,它将每个向量 T(v)T(\boldsymbol v)T(v) 变换回 v\boldsymbol vv:T−1(T(v))=v对应矩阵的乘积A−1(Av)=vT^{-1}(T(\boldsymbol v))=\boldsymbol v\kern 18pt对应矩阵的乘积\kern 19ptA^{-1}(A\boldsymbol v)=\boldsymbol vT−1(T(v))=v对应矩阵的乘积A−1(Av)=v如果 T(v)=Av,S(u)=BuT(\boldsymbol v)=A\boldsymbol v,S(\boldsymbol u)=B\boldsymbol uT(v)=Av,S(u)=Bu,则乘积 T(S(u))T(S(\boldsymbol u))T(S(u)) 对应乘积 ABuAB\boldsymbol uABu.
下面讨论一个无可避免的问题:所有的从 V=Rn\textrm{\pmb{V}}={\textrm {\pmb R}}^nV=Rn 到 W=Rm\pmb {\textrm W}=\pmb{\textrm R}^mW=Rm 的线性变换都可以由矩阵给出吗? 当线性的 TTT 是 “旋转” “投影” 或其它的变换,TTT 总是有对应的矩阵 AAA 吗?T(v)T(\boldsymbol v)T(v) 总是 AvA\boldsymbol vAv 吗?
答案是肯定的!这是不从矩阵开始的线性代数的一种方法。在我们选择好一组输入基和输出基后,我们可以通过矩阵来描述线性变换。
注: 变换有自己的语言。从矩阵角度来看线性变换 T(v)=AvT(\boldsymbol v)=A\boldsymbol vT(v)=Av,矩阵 AAA 的列空间包含所有的输出 AvA\boldsymbol vAv,零空间包含所有的使 Av=0A\boldsymbol v=\boldsymbol 0Av=0 时的输入;在变换语言中,这些对应的分别是 “值域(range)” 与 “核(kernel)”:
T 的值域:\color{blue}T\,的值域:T的值域: 所有的输出 T(v)T(\boldsymbol v)T(v). 值域对应列空间。
T 的核:\color{blue}T\,的核:T的核:所有使得 T(v)=0T(\boldsymbol v)=\boldsymbol 0T(v)=0 的输入. 核对应零空间。
值域在输出空间 W\textrm {\pmb W}W 中,核在输入空间 V\textrm{\pmb V}V 中,当 TTT 是用一个矩阵左乘,即 T(v)=AvT(\boldsymbol v)=A\boldsymbol vT(v)=Av 时,值域是列空间,核是零空间。
四、平面的线性变换
观察线性变换的作用比起定义它要更有趣。当一个 2×22\times22×2 的矩阵 AAA 左乘 R2\textrm{\pmb R}^2R2 中的所有向量时,我们可以观察它是如何作用的。我们下面以一个有 111111 个顶点的 “房子” 为例,这 111111 个向量 v\boldsymbol vv 变换成 111111 个向量 AvA\boldsymbol vAv,连接 v\boldsymbol vv 的直线变换成了连接 AvA\boldsymbol vAv 的直线(从房子到房子的变换是线性的!)。对一个标准的房子应用 AAA 会产生一个新房子 —— 可能伸缩或旋转或其它的不适合居住的房子。
这一部分是可视化的图像,不属于理论。下面展示了 444 个房子和用于生成它们的矩阵。HHH 的列是第一个房子的 111111 个顶点(HHH 是 2×122\times122×12 的,以便于 plot2d 连接第 111111 个顶点和第 111 个顶点),AAA 左乘房子矩阵 HHH 的 111111 个顶点将得到变换后房子 AHAHAH 的顶点。
房子矩阵H=[−6−6−70766−3−300−6−721812−7−7−2−2−7−7]\pmb{房子矩阵}\kern 16ptH=\begin{bmatrix}-6&-6&-7&0&7&6&\kern 7pt6&-3&-3&\kern 7pt0&\kern 7pt0&-6\\-7&\kern 7pt2&\kern 7pt1&8&1&2&-7&-7&-2&-2&-7&-7\end{bmatrix}房子矩阵H=[−6−7−62−710871626−7−3−7−3−20−20−7−6−7]
MATLAB 中画出标准房子的程序:
H = [-6 -6 -7 0 7 6 6 -3 -3 0 0 -6;-7 2 1 8 1 2 -7 -7 -2 -2 -7 -7];
x = H(1,:)'; y = H(2,:)';
axis([-10 10 -10 10]), axis('square') % 坐标范围是x轴-10~10,y轴-10~10,坐标区域显示为正方形
plot(x, y,'o', x, y, '-'); % 连接线是实线,顶点是圆圈

五、主要内容总结
- 变换 TTT 将每个输入空间中的 v\boldsymbol vv 映射为输出空间中的 T(v)T(\boldsymbol v)T(v).
- 若 T(v+w)=T(v)+T(w)T(\boldsymbol v+\boldsymbol w)=T(\boldsymbol v)+T(\boldsymbol w)T(v+w)=T(v)+T(w) 且 T(cv)=cT(v)T(c\boldsymbol v)=cT(\boldsymbol v)T(cv)=cT(v),则 TTT 是线性的:直线映射为直线。
- 线性变换将线性组合映射为线性组合:T(c1v1+c2v2+⋯+cnvn)=c1T(v1)+c2T(v2)+⋯+cnT(vn)T(c_1\boldsymbol v_1+c_2\boldsymbol v_2+\cdots+c_n\boldsymbol v_n)=c_1T(\boldsymbol v_1)+c_2T(\boldsymbol v_2)+\cdots+c_nT(\boldsymbol v_n)T(c1v1+c2v2+⋯+cnvn)=c1T(v1)+c2T(v2)+⋯+cnT(vn).
- TTT 为求导,T+T^+T+ 为积分都是线性的。AAA 为 m×nm\times nm×n 的矩阵,则 T(v)=AvT(\boldsymbol v)=A\boldsymbol vT(v)=Av 是将 Rn\textrm{\pmb R}^nRn 映射成 Rm\pmb {\textrm R}^mRm.
六、例题
【例8】消元矩阵 A=[1011]A=\begin{bmatrix}1&0\\1&1\end{bmatrix}A=[1101] 给出一个从 (x,y)(x,y)(x,y) 到 T(x,y)=(x,x+y)\pmb{T(x,y)=(x,x+y)}T(x,y)=(x,x+y) 的剪切变换(shearing transformation). 如果输入向量填满一个正方形,画出变换后的正方形。
解: xxx 轴上的点 (1,0)(1,0)(1,0) 和 (2,0)(2,0)(2,0) 进行 TTT 变换后是与 xxx 轴成 45°45°45° 角直线上的点 (1,1)(1,1)(1,1) 和 (2,2)(2,2)(2,2). yyy 轴上的点没有移动:T(0,y)=(0,y)T(0,y)=(0,y)T(0,y)=(0,y),这个是 λ=1\lambda=1λ=1 的特征向量。垂直的线向上滑动,这就是剪切,因此正方形变成了平行四边形。

【例9】若要非线性变换 TTT 可逆,那么需要输出空间中的每个向量 b\boldsymbol bb 都恰好对应输入空间的一个 x\boldsymbol xx:T(x)=bT(\boldsymbol x)=\boldsymbol bT(x)=b 总是恰好有一个解。下面这些变换(xxx 为实数)哪些是可逆的?若可逆,则 T−1T^{-1}T−1 是什么?它们不是线性的,甚至 T3T_3T3 也不是。 当求解 T(x)=bT(\boldsymbol x)=\boldsymbol bT(x)=b 时,就是在求 TTT 的逆:T1(x)=x2T2(x)=x3T3(x)=x+9T4(x)=exT5(x)=1x(x≠0)\color{blue}T_1(x)=x^2\kern 10ptT_2(x)=x^3\kern 10ptT_3(x)=x+9\kern 10ptT_4(x)=e^x\kern 10ptT_5(x)=\frac{1}{x}(x\neq0)T1(x)=x2T2(x)=x3T3(x)=x+9T4(x)=exT5(x)=x1(x=0)解: T1T_1T1 不可逆:x2=1x^2=1x2=1 有两个解并且 x2=−1x^2=-1x2=−1 无解。
T4T_4T4 不可逆因为 ex=−1e^x=-1ex=−1 无解。(如果输出空间改为正数 bbb,则 ex=be^x=bex=b 的逆就是 x=lnbx=\ln bx=lnb.)
注意 T52(x)=1T^2_5(x)=1T52(x)=1(取两次倒数)是恒等变换,但是 T32(x)=x+18T_3^2(x)=x+18T32(x)=x+18,T22(x)=x9T_2^2(x)=x^9T22(x)=x9,T42(x)=eexT_4^2(x)=e^{e^x}T42(x)=eex.
T2,T3,T5T_2,T_3,T_5T2,T3,T5 可逆:x3=b,x+9=bx^3=b,x+9=bx3=b,x+9=b 和 1x=b\displaystyle\frac{1}{x}=bx1=b 都只有一个解:x=T2−1(b)=b1/3x=T3−1(b)=b−9x=T5−1(b)=1b\color{blue}x=T_2^{-1}(b)=b^{1/3}\kern 10ptx=T_3^{-1}(b)=b-9\kern 10ptx=T_5^{-1}(b)=\frac{1}{b}x=T2−1(b)=b1/3x=T3−1(b)=b−9x=T5−1(b)=b1
【例10】HHH 是一个房子图形的矩阵,可以使用下面的函数 plot2d(H) 来绘制这个房子:房子矩阵H=[−6−6−70766−3−300−6−721812−7−7−2−2−7−7]\pmb{房子矩阵}\kern 16ptH=\begin{bmatrix}-6&-6&-7&0&7&6&\kern 7pt6&-3&-3&\kern 7pt0&\kern 7pt0&-6\\-7&\kern 7pt2&\kern 7pt1&8&1&2&-7&-7&-2&-2&-7&-7\end{bmatrix}房子矩阵H=[−6−7−62−710871626−7−3−7−3−20−20−7−6−7]
function [] = plot2d(H) % 定义函数 plot2d,输入参数是 H,无输出参数
x = H(1,:)'; y = H(2,:)';
axis([-10 10 -10 10]), axis('square')
plot(x, y, 'o', x, y, '-'); % 'o' 表示圆圈,'-' 表示实线段
end
(1)使用 plot2d(H) 画出这个房子矩阵的图,并画出以下矩阵作用后的图 plot2d(DH),plot2d(BH),plot2d(U*H):D=[2001]B=[0.70.70.30.3]U=[1101]D=\begin{bmatrix}2&0\\0&1\end{bmatrix}\kern 10ptB=\begin{bmatrix}0.7&0.7\\0.3&0.3\end{bmatrix}\kern 10ptU=\begin{bmatrix}1&1\\0&1\end{bmatrix}D=[2001]B=[0.70.30.70.3]U=[1011](2)设变换 TTT 满足 T(v)=−v+(1,0)T(\boldsymbol v)=-\boldsymbol v+(1,0)T(v)=−v+(1,0) 时,则经过此 “仿射变换” 后的图形如何?
(3)使用 Figure 8.2 中的矩阵来测试 plot2d(A’ * H) 和 plot2d(A’ * A * H).
解: 下面是 MATLAB画出这些图形的程序:
H = [-6 -6 -7 0 7 6 6 -3 -3 0 0 -6;
-7 2 1 8 1 2 -7 -7 -2 -2 -7 -7];
figure('Name','原始房子H','NumberTitle','off');
plot2d(H);
D = [2 0; 0 1];
figure('Name','对角矩阵作用D*H','NumberTitle','off');
plot2d(D*H);
B = [0.7 0.7; 0.3 0.3];
figure('Name','秩一矩阵作用B*H','NumberTitle','off');
plot2d(B*H);
U = [1 1; 0 1];
figure('Name','上三角矩阵作用U*H','NumberTitle','off');
plot2d(U*H);
figure('Name','仿射变换T(v)=-v+(1,0)','NumberTitle','off');
plot2d(-H + [1;0]);
A = [cosd(35) -sind(35); sind(35) cosd(35)]; % cosd(),sind()为直接输入角度的函数
figure('Name','旋转矩阵的转置','NumberTitle','off');
plot2d(A'*H);
figure('Name','旋转矩阵的A''*A','NumberTitle','off');
plot2d(A'*A*H);
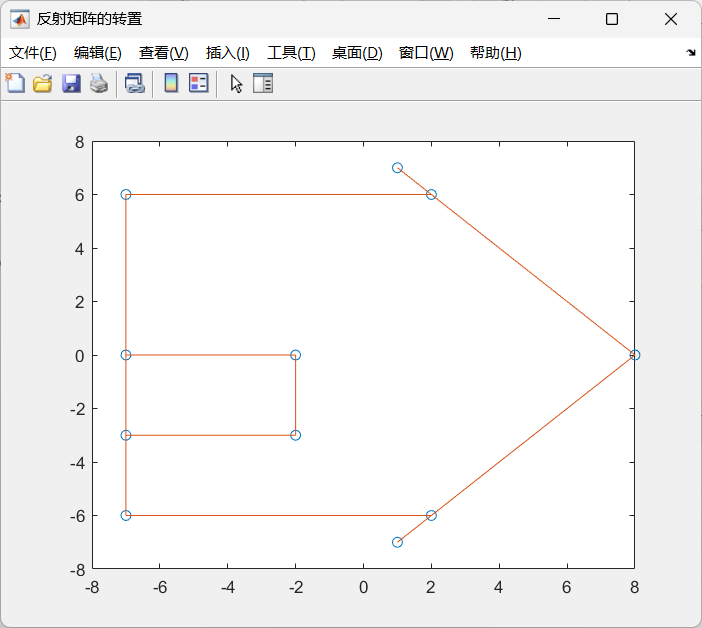
A = [0 1; 1 0]; % 反射矩阵
figure('Name','反射矩阵的转置','NumberTitle','off');
plot2d(A'*H);
figure('Name','反射矩阵的A''*A','NumberTitle','off');
plot2d(A'*A*H);
A = [0.7 0.3; 0.3 0.7]; % 马尔可夫矩阵
figure('Name','马尔可夫矩阵的转置','NumberTitle','off');
plot2d(A'*H);
figure('Name','马尔可夫矩阵的A''*A','NumberTitle','off');
plot2d(A'*A*H);
(1)MATLAB运行的图像如下:
 |  |
 |  |
(2)仿射变换:

(3)矩阵的转置:
 |  |
 |  |
 |  |
【例11】下面代码是先创建一个包含 50 个角度的向量 theta, 然后生成一个单位圆,再使用变换 T(v)=AvT(\boldsymbol v) = A\boldsymbol vT(v)=Av 将这个单位圆变换成椭圆。最后绘制出这个单位圆和椭圆。
A = [2 1;1 2]; % 变换矩阵A
theta = 0:2*pi/50:2*pi; % 0~2π共50个角度的theta向量
circle = [cos(theta); sin(theta)]; % 单位圆矩阵
ellipse = A * circle; % 变换成椭圆
axis([-4 4 -4 4]); axis('square');
plot(circle(1, :), circle(2, :), ellipse(1, :), ellipse(2, :)) % 绘制单位圆和变换后的椭圆,其中circle(1, :)表示矩阵第一列的所有数据,此处是横坐标
解: 下面是 MATLAB运行后的图形






















 1089
1089

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








