树和二叉树

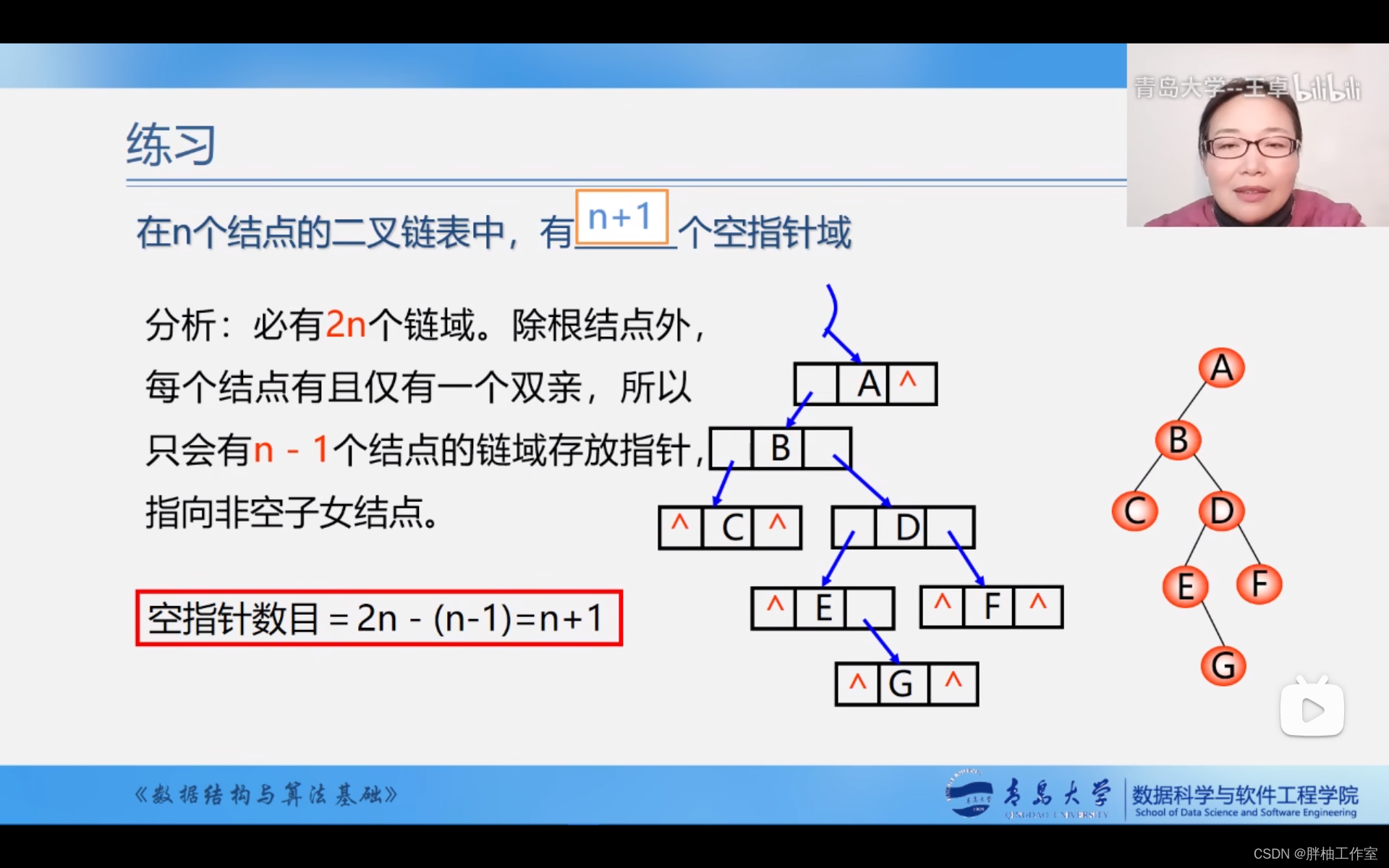
一、定义及基本术语

详见书本P111~113
二叉树不是树的特殊情况，它们是两个概念，但有关树的基本术语对二叉树都适用。

二叉树的子树一定要区分左子树还是右子树，即使只有一棵子树也一定要说明是左子树还是右子树，树只有一个孩子的时候，就不用区分左右的次序了，下图很好解释了这种区别

二、二叉树的性质和存储结构

（其他理论知识参考书本P118~121）

中序遍历的非递归算法：（以此为准）

void InOrder_unrec(BiTree T)
{
SqStack S;
InitStack(&S);
BiTree p = T;
//BiTree pop = NULL;
while (p || !IsEmpty(&S))
{
	if(p)
	{
//栈顶元素始终是p的parent节点
	Push(&S,p);
	p = p->lchild;
	}
	else
	{
	Pop(&S, &p);
//把栈顶元素弹出给p，此时变成了原p的parent
//此时p的左孩子为空，根据in-oder规则，输出根节点p，然后再以相同的方式遍历他的右孩子
	printf("%c", p->data);
	p = p->rchild;
//输出根节点后，遍历其右子树
	}
  }
}

二叉树的层次遍历算法：
对于一颗二叉树，从根节点开始，按照从上到下，从左到右的顺序进行访问，每个结点仅仅访问一次。

void LevelOrer(BiTree T)
{
	BiTree temp = NULL;
	SqQueue Q;
	InitQueue(&Q);
	if(T) //先入队根
	EntryQ(&Q, T);
	while(!IsEmpty(&Q))
{
	OutQ(&Q, &temp); //temp暂存弹出值
	printf("%c", temp->data); //输出
	if (temp->lchild) //在入队temp的左孩子和右孩子
	EntryQ(&Q, temp->lchild);
	if (temp->rchild) EntryQ(&Q, temp->rchild);
  }
}

先序遍历算法建立二叉树

void Creat_BiTree_Pre(BiTree *T)//T是二级指针
{
//根据输出字符识别虚空节点，'#'代表虚空节点
char e;
scanf("%c", &e);
if('#' == e)
*T = NULL; //设置虚空节点
else
{  
	*T =(BiTree)malloc(sizeof(BiNode));
	(*T)->data = e;
	Creat_BiTree_Pre(&(*T)->lchild); //传入参数时需传入二级指针，原本lchild是一级指针，加了&后变成二级指针。
	Creat_BiTree_Pre(&(*T)->rchild);//递归算法
  }
}

复制二叉树（先序遍历，从根节点开始复制，按照“根-左-右”的顺序进行复制）

//复制二叉树算法
void Copy (BiTree T, BiTree *NewT) {
    if (T==NULL) {
     *NewT = NULL;  return;
    }
    else {
        *NewT = new BiTNode; 
        (*NewT)->data = T->data;
        Copy(T->lchild, &(*NewT)->lchild);
        Copy(T->rchild, &(*NewT)->rchild);
    }
}

二叉树的深度：

int Depth(Bitree T){
	if (!T) return 0;
	else 
	{
		int m = Depth(T->lchild);
		int n = Depth(T->rchild);
		return m > n ? (m + 1) : (n + 1);
	}
} 

求二叉树的叶子结点数：

int Leafcount(Bitree T){
	if (!T) return 0;//空树没有叶子结点 
	if (T->lchild == NULL && T->rchild == NULL) return 1;//只有左右孩子均为空时才是叶子结点 
	else return Leafcount(T->lchild) + Leafcount(T->rchild);//左右子树的叶子结点数求和（根节点一定不是叶子结点） 
} 

线索二叉树（详见书本P128~）

树的孩子表示法：

其他具体实例见书本P134~135

三、树、二叉树、森林的相互转化

将树转换成二叉树:
加线：在兄弟之间加一连线
抹线：对每个结点，除了其左孩子，去除其与其余孩子之间的关系
以根节点的左孩子为中心，顺时针旋转45°
兄弟相连留长子

将二叉树转换成树:
加线：若p结点是双亲结点的左孩子，则将p的右孩子，右孩子的右孩子…沿着分支找到所有右孩子，都与p的双亲用线连起来
抹线：抹掉原来二叉树中双亲与右孩子之间的连线
调整：将结点按层次排序，形成树结构
左孩右右连双亲，去掉原来右孩线

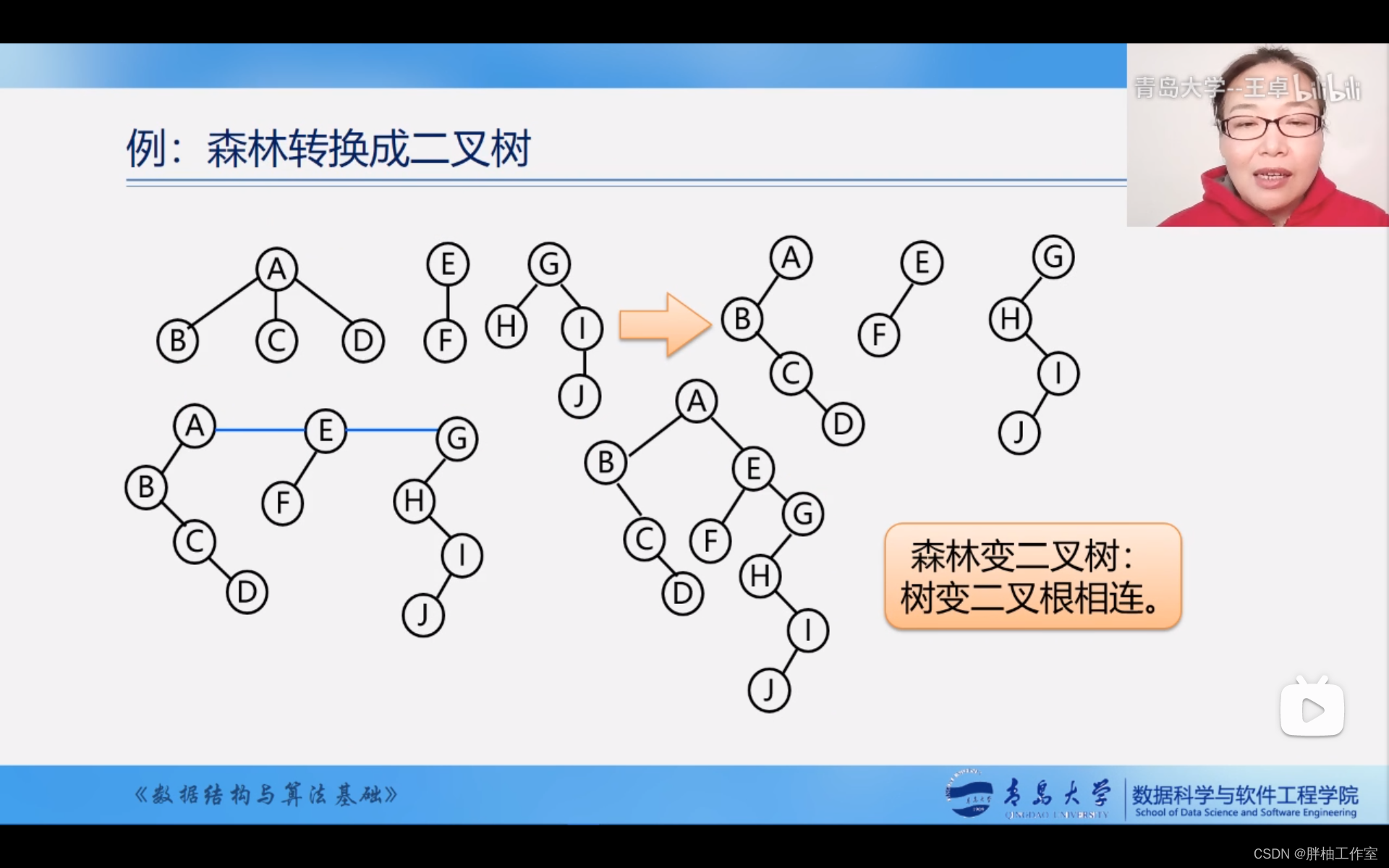
森林变二叉树
1、将各棵树分别转换成二叉树
2、将每棵树的根结点用线相连
3、以第一棵树根结点作为二叉树的根，再以根结点为轴心，顺时针旋转，构成二叉树型结构
树变二叉根相连

二叉树变森林
1、抹线：将二叉树中根结点与其右孩子连线，及沿右分支搜索到的所有右孩子之间的连线全部抹掉，使之变成孤立二叉树
2、还原：将孤立的二叉树还原成树
去掉全部右孩线，孤立二叉再还原

四、树和森林的遍历

树的遍历：
1、先根遍历：若树不为空，则先访问根节点，然后再依次先根遍历遍历各个子树
2、后根遍历：若树不为空，先依次后根遍历各个子树，再访问根节点
3、层次遍历：自上到下，从左到右

森林的遍历：

先序遍历：（每一棵树从左到右进行先根遍历）
森林非空，则：
1、访问森林第一棵树的根结点
2、前序遍历森林中第一棵树的子树森林
3、先序遍历森林中（除第一棵树之外）其余树构成的森林
中序遍历：（每一棵树从左到右进行后根遍历！）
森林非空，则：
1、中序遍历森林中第一棵树的子树森林
2、访问森林中第一棵树的根结点
3、中序遍历森林中（除第一棵树之外）其余树构成的森林

示例：

五、哈夫曼树

5.1、基本概念及构造（见书本P136~137）

构造示例2：

构造二叉树的代码如下：

//哈夫曼树构造算法实现
void CreatHuffmanTree(HuffmanTree *HT, int n) {//构造哈夫曼树——哈夫曼算法
    if (n <= 1) return;
    int m = 2 * n - 1;//数组共有m个元素
    HT = new HTNode[m + 1]; //0号不用，HT[m]表示根结点
    //或：HT = (HuffmanTree)malloc(sizeof(HTnode) * (m + 1));
    for (int i = 1; i <= m; i++) {
        (*HT)[i].lch = (*HT)[i].rch = (*HT)[i].parent = 0;
    }//将2n-1个元素的lch，rch，parent初始化为0
    for (int i = 1; i <= n; i++) cin >> (*HT)[i].weight;
    //初始化步骤结束
    for (int i = n + 1; i <= m; i++) {//合并产生n-1个结点——构造哈夫曼树
    	Select(*HT, i-1, s1, s2); 
    //在HT[K](1 <= K <= i - 1)中选择两个其双亲域是0，且权重最小的结点，返回它们的序列号s1, s2
      	(*HT)[s1].parent = (*HT)[s2].parent = i;//表示F中删除s1,s2
        (*HT)[i].lch = s1; (*HT)[i].rch = s2;//s1,s2分别作为i的左孩子和右孩子
        (*HT)[i].weight = (*HT)[s1].weight + (*HT)[s2].weight;//i的权重为左右孩子权重之和
    }
}

select函数代码实现如下：

void Select(const HTree T, int length, int *e1, int *e2)
{
	int min1, min2;
	min1 = min2 = INT_MAX;//2^31,常用于求最小值；此外，INT_MIN为-2^31，常用于求最大值
	int pos1, pos2;
	pos1 = pos2 = 0;
	for (int i = 1; i <= length; ++i)
{
		if (T[i].parent == 0)
	{
	//!parent == 0说明是根节点
			if (T[i].weight < min1)
		{
			min2 = min1;
			pos2 = pos1;
			min1 = T[i].weight;
			pos1 = i;
		}
		else if (T[i].weight < min2)
		{
			min2 = T[i].weight;
			pos2 = i;
		}
	}
}
	*e1 = pos1;
	*e2 = pos2;
}