基于ABAQUS的岛桥结构仿真方法

基于ABAQUS的可拉伸柔性传感器网络屈曲与后屈曲分析方法

摘要

飞机智能蒙皮技术要求在飞机结构中集成大规模轻量级传感器网络。为满足这些需求，采用了岛桥结构设计，使得传感器网络可以小规模制造并大规模扩展。目前针对岛桥结构的力学性能已开展了理论分析、有限元仿真和实验验证。然而，理论分析难以处理不规则形状结构，而现有的仿真研究主要集中在单个单元的岛桥结构，缺乏对网络的整体分析。本文提出了基于ABAQUS的岛桥结构网络有限元仿真方法，包括屈曲模态分析和后屈曲变形分析。通过屈曲模态分析提取结构的初始屈曲变形状态，并通过后屈曲变形分析获得结构的后屈曲变形状态。该仿真方法应用于不同类型岛桥结构网络（包括蛇形、分形和不规则岛桥结构网络）的力学性能和变形模式分析。结果表明，所提出的仿真方法能够有效指导可拉伸传感器网络的设计。

关键词 —飞机智能蒙皮，结构健康监测，传感器网络，柔性与可拉伸，岛桥结构，仿真方法

一、引言

飞机智能蒙皮是未来飞机的一项先进技术。结构健康监测（SHM）是飞机智能蒙皮的关键功能之一[1‐2]。在现有的SHM技术中，压电（PZT）传感器网络与基于导波的监测相结合的方法广受欢迎[3‐5]。然而，对于大面积航天结构而言，人工布置传感器耗时且效率低下。此外，还存在传感器一致性差以及导线引起的附加重量等问题。通过柔性印刷电路（FPC）工艺，可将压电传感器和导线集成制造，也称为SMART层[6‐7], ，从而简化布线布局、降低网络重量，并保证PZT的一致性。然而，由于制造工艺的限制，直接制造大面积传感器网络非常困难。

近年来，柔性与可拉伸电子技术在医疗、通信和娱乐领域得到了广泛的研究和应用，例如电子皮肤[8],笔形柔性显示器[9]等。基于柔性电子技术，传感器网络可以实现柔性与可拉伸化，并可实现“小规模制造、大规模扩展”的应用，有利于在大面积航空结构上布置传感器网络。

为了使传感器网络不仅具有良好的柔性与拉伸性，还具备信号传输能力，许多学者对岛桥结构进行了研究。在岛桥结构中，岛用于布置传感器，而桥则用于布置信号传输导体。近年来，关于岛桥结构的研究主要集中在具有优良拉伸性的蛇形和分形岛桥结构上，其互连结构分别为蛇形线和分形线。Zhang et al. [10‐11]提出了一个用于研究蛇形和自相似分形互连的力学模型，并通过该模型分析了结构可拉伸性与几何参数之间的关系。基于曲梁理论和平面应变假设，Widlund et al. [12]研究了蛇形几何形状与其力学性能之间的关系。除了理论分析外，许多学者也通过有限元仿真来研究岛桥结构。Zhang et al. [13‐14]基于分形岛桥结构设计了可拉伸电池，并提出了一种针对分形岛桥结构的仿真方法，其计算速度比传统方法更快。基于ABAQUS，Wang et al. [15‐16]提出了蛇形和分形岛桥结构的仿真方法，并对设计的大规模可拉伸传感器网络进行了分析。类似地，Guo和Kim et al. [17]通过对单单元岛桥结构的拉伸变形仿真，分析了传感器网络设计对结构应变减小的影响。然而，以往的研究存在两个主要缺陷：第一，理论模型难以分析任意不规则形状岛桥结构的应力、应变和变形；第二，现有的仿真方法主要集中于仅含单个单元的岛桥结构，无法充分考虑结构网络的整体变形。

本文针对以往研究中的不足，提出了基于 ABAQUS的岛桥结构网络仿真方法，可为可拉伸传感器网络的设计与开发提供指导。基于该仿真方法，获得了拉伸过程中岛桥结构网络的应力、应变分布、拉伸性及变形状态，并进行了分析，包括 1×3阵列蛇形岛桥结构、 2×3阵列蛇形岛桥结构、 2×2阵列分形岛桥结构和 2×2阵列不规则岛桥结构。

II. 岛桥结构网络的仿真方法

A. 仿真模型与方法

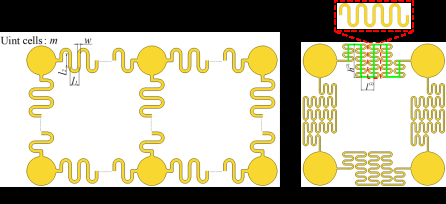
由于蛇形和分形互连结构具有良好的拉伸性，本文主要关注蛇形和分形岛桥结构网络的仿真方法。根据岛状区域的阵列排列，岛桥结构网络可描述为：1×3阵列式蛇形岛桥结构、2×3阵列式蛇形岛桥结构、2×2阵列式分形岛桥结构和2×2阵列式不规则岛桥结构。蛇形和分形几何结构如图1所示。蛇形几何由以下五个几何参数确定：宽度w、厚度t、单元数量m、半圆形弧直径l1,直线段l2。分形互连为基于二阶蛇形的分形互连，结构的整体尺寸由高度h(2)和间距 l(2)控制，局部尺寸由蛇形互连结构控制。

在屈曲变形过程中，蛇形和分形互连不仅会发生大变形和位移，还会产生大转动变形，这是一个几何非线性问题。针对上述问题，ABAQUS有限元分析软件具有良好的仿真效率和精度。基于ABAQUS的岛桥结构网络的仿真方法主要包括两个方面：屈曲模态分析和后屈曲变形分析。当岛桥结构网络受到面内拉伸载荷作用时，由于其宽厚比较大，以及潜在的材料缺陷和外部扰动，互连结构容易发生面外屈曲，并呈现出不同的屈曲模式。通过屈曲模态分析，可以提取出互连结构的不同屈曲模式，反映互连可能的变形趋势。进一步地，在后屈曲变形分析中将屈曲模式作为初始缺陷引入，以确保仿真结果的准确性。引入屈曲模式后，可通过后屈曲变形分析获得结构的变形状态以及结构应力、应变和位移分布。仿真流程如图2所示。

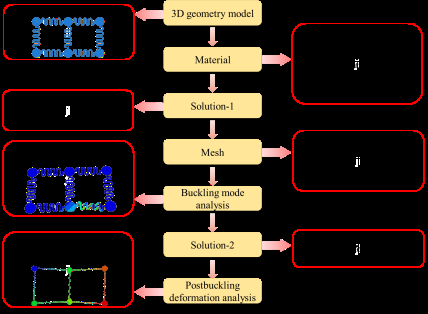
1) 三维几何模型和材料属性：

可在 ABAQUS 的 “Part”模块中创建三维几何模型。由于通常使用柔性印刷电路板（FPC）来制造传感器网络，且聚酰亚胺常作为基底材料，因此本仿真中采用聚酰亚胺（PI）。PI 的弹性应变极限为 2%~3%，本文中取为 2%。仿真仅需获得结构在 PI 弹性应变极限下的变形状态，为简化仿真过程，可将材料视为理想弹塑性材料。此外，在设置材料属性时，ABAQUS 中计算单位的统一对于仿真至关重要。具体参数如下：弹性模量 2500 MPa，泊松比 0.34，屈服应力和对应的屈服应变为 120 MPa 和 0。

2) 求解设置：

求解设置包括步骤、载荷和边界条件。此外，屈曲模态分析和后屈曲变形分析的求解设置不同，将在下文进一步讨论。

3) 网格划分：

单元形状设置为“六面体”，单元类型为八节点三维缩减积分沙漏控制实体单元（C3D8R）。在设置全局种子时，全局近似尺寸设为0.1，最大偏差因子设为0.01，以保证单元尺寸适中且分布合理。对于简单蛇形互连，仿真速度较快；而对于复杂分形互连，则有助于仿真易于收敛。此外，需对变形较小的岛状区域进行局部种子设置，以提高仿真速度。需要注意的是，在完成网格划分后必须进行网格检查，确认无错误和警告后方可进行仿真。

B. 屈曲模态分析

屈曲模态分析的步骤为“屈曲”步，通过屈曲模态分析可获得屈曲模式及相应的临界载荷（特征值与集中力的乘积）。在步长设置中，请求的特征值数量应尽可能大，以确保获得所需的屈曲模式。在屈曲模态分析过程中，还需输出各屈曲模式的位移值，用于后屈曲变形分析。

为了确保结构的仿真与实际拉伸情况一致，应对岛桥结构网络两端或对角角落的岛状区域进行约束。其中一个岛状区域完全固定，其他岛状区域在同一水平面上被拉伸，其余岛状区域自由。在最右侧或底部的岛状区域施加集中力。此外，为了防止局部变形过大导致非收敛，需通过方程约束将集中力作用点与岛状区域耦合。

C. 后屈曲变形分析

后屈曲变形分析的步骤为“静态,Riks”步骤。在仿真之前，为了在模型复制中给结构施加初始缺陷，需采用对应于每个最小正特征值的屈曲模式需要分别引入独立互连，这是单轴拉伸过程中最早的屈曲变形状态。引入屈曲模式位移的方法是在语句“ *End Assembly”之后添加语句“*imperfection, file=buckle, step=1(new line) 9,0.05”。其中，“ buckle”是屈曲模态分析的作业名称，而“9,0.05”表示将屈曲模式9的5%位移值作为初始缺陷引入。

结构的后屈曲变形不再满足小变形假设，因此需要在步长设置中开启“NIgeom”。终止标准中的最大荷载比例系数设置为1，最大增量步数应尽可能设大，以确保结构变形足够大。此外，初始弧长增量应小于临界载荷，最小和最大弧长增量应合理设置，以保证仿真过程中弧长增量在其范围内。对于后屈曲变形分析，边界条件设置保持不变，但载荷的大小应根据仿真的实际情况进行调整。

如果在仿真的初期阶段出现大量负增量步，甚至不收敛，且结构无法完全屈曲和展开，则可以通过适当减小载荷大小或增加初始缺陷使仿真顺利进行。此外，如果仿真中出现错误信息“在Riks步的第一次迭代中发现零位移解”，则可通过调整网格尺寸和载荷获得更大的结构变形。

III. 蛇形岛桥结构网络仿真分析

A. 1×3阵列蛇形岛桥结构

在本仿真中，厚度t为0.05 mm，宽度w为0.4 mm，单元数量m为4，半圆弧直径l1为1.2 mm，直线段长度l2为1.8 mm。此外，岛半径为2 mm，蛇形与岛连接处的半径为0.1 mm。岛的中心间距（30 mm）可视为蛇形互连两端的初始长度。整体拉伸应变定义为结构伸长量与初始长度之比，用于表示结构的拉伸变形程度。当结构应变达到最大弹性应变时，对应的整体拉伸应变即被视为该结构的拉伸性。

1×3阵列蛇形岛桥结构具有对称与反对称形式，可以解释为互连相对于中间岛呈对称和非对称，如图3所示。中间岛可视为互连的一部分，因此1×3蛇形岛桥结构仅有一个独立互连。

在屈曲模态分析中，请求的特征值数量设置为20，集中力为1牛顿，力的方向为拉伸方向。在后屈曲变形分析中，引入屈曲模式5%的位移值作为初始缺陷，集中力为0.1牛顿。此外，在步长设置中，最大增量步数为1000，初始弧长增量为1E‐5，最小弧长增量为1E‐25，最大弧长保持不变。

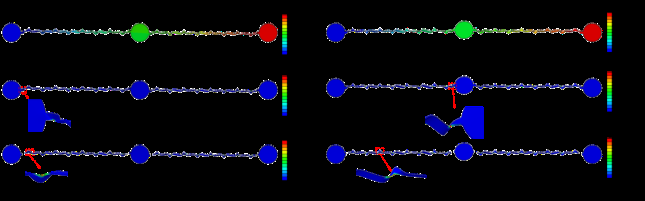
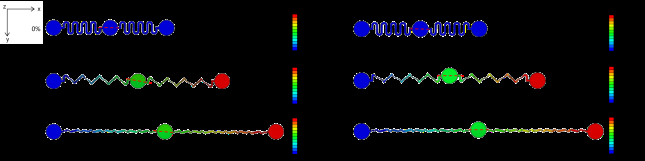
通过仿真可以获得结构的位移和应变分布，用于研究结构的变形状态和拉伸性。对称结构与非对称结构的拉伸性基本相同，如图4和图5所示。当结构的最大应变达到约2%时，整体拉伸应变为90%，最大应变位置位于岛与蛇形连接处。由于圆弧半径过小，在连接处产生应力集中，导致应变较大。实际上，通过增大圆弧半径可以减小应变，因此可将连接处区域隐藏进行分析。在此之后，当整体拉伸应变约为90%时，结构的最大应变仅为1.3%，位于蛇形弧顶处。此外，当结构的最大应变为 2%时，结构的整体拉伸应变约为95%，因此该结构的拉伸性可达约95%。

拉伸过程中，对称与非对称结构网络的中间岛旋转情况不同。如图6所示，非对称结构的中间岛最大旋转角度可超过10°，而对称结构的中间岛旋转角度非常小。因此，非对称结构不利于方向‐敏感型传感器（如应变传感器）的应用。

B. 2×3阵列蛇形岛桥结构

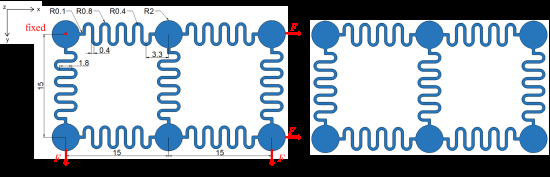
在 2×3阵列蛇形岛桥结构中，蛇形互连的几何参数与上述相同，也存在对称与反对称形式，如图7所示。初始时， 2×3阵列蛇形岛桥结构覆盖一个30 mm×15 mm的矩形区域，该区域作为衡量结构扩展程度的参考。

中间岛通过蛇形互连连接，由于变形协调，中间岛两端的四个蛇形互连以及中间岛之间的互连在结构变形时会相互影响。该结构可视为具有三个独立互连。

在屈曲模态分析中，请求的特征值数量设置为40，集中力设置为1牛顿。在后屈曲变形分析中，引入屈曲模式的5%和10%的位移值作为初始缺陷，分别对应对称结构和反对称结构，力设置为0.1牛顿。此外，在步长设置中，初始弧长增量设置为1E‐5，其他设置与1×3阵列蛇形岛桥结构相同。

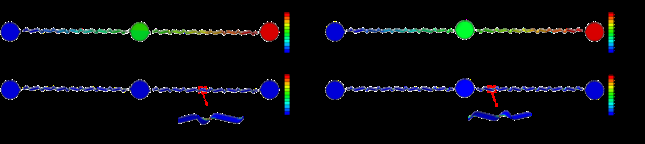
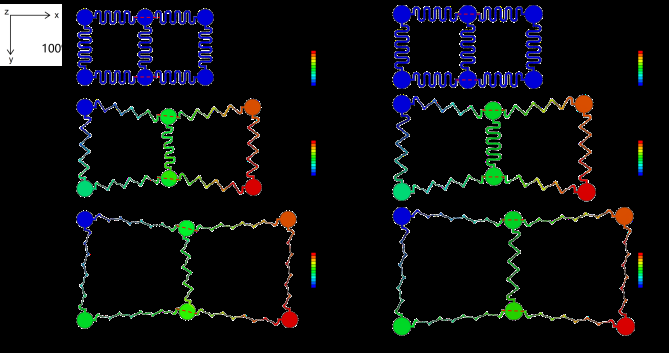
类似地，非对称结构与对称结构的拉伸性基本相同，如图8所示。当结构扩展到其初始面积的360%时，结构的最大应变约为2%，最大应变位置位于蛇形互连与岛状区域的连接处。此外，在隐藏连接处后，结构的最大应变降低至1.3%，且最大应变位置也转移到蛇形弧顶处。

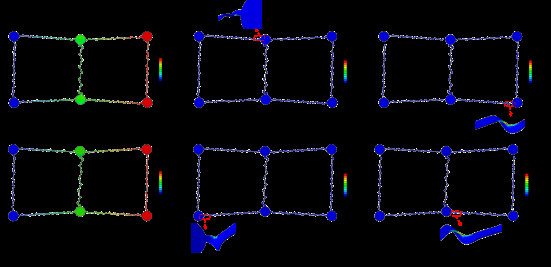
在拉伸过程中，对称结构和非对称结构的中间岛旋转情况也不同。如图9所示，在拉伸过程中，对称结构中间岛的最大旋转角度仅为1°，而反对称结构中间岛的最大旋转角度达到约15°。同样，如果将方向敏感传感器放置在反对称结构上，测量结果将受到很大影响。

IV. 分形岛桥结构网络仿真分析

A. 2×2阵列分形岛桥结构

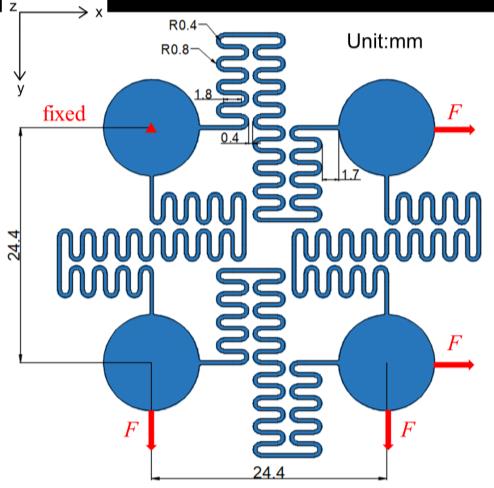
互连结构为基于蛇形的二阶分形互连结构。如图10所示，从整体来看，该分形互连可视为仅包含一个单元的蛇形互连，其局部直线段由包含四个单元的蛇形互连构成，局部蛇形互连的尺寸已在上文描述。该结构所包围的初始面积为24.4 mm×24.4 mm，可作为描述结构扩展程度的参考。

四个岛状区域仅在同一水平面上被拉伸，互连结构的变形仅受两个岛状区域之间拉伸程度的影响。因此，2×2阵列分形岛桥结构具有四个独立互连结构。

在屈曲步设置中，请求的特征值数量设置为40。在后屈曲变形步设置中，初始弧长增量设置为1E‐6，其余设置与上述相同。在进行后屈曲变形分析之前，必须将屈曲模式的50%位移值作为初始缺陷引入。屈曲模态分析中的力设置为1牛顿，后屈曲变形分析中的力设置为0.02牛顿。

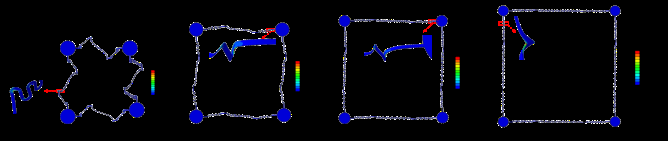
仿真结果如图11所示。当结构被拉伸至初始面积的2500%时，最大应变为0.65%，位于互连内弧的顶部。可以看出，分形互连的拉伸性远大于蛇形互连，且最大应变位置位于内弧顶部。

由于屈曲临界载荷出现的顺序不同，屈曲变形出现的顺序也不同。此外，在出现屈曲变形后，结构的应变能会降低。因此，在相同力的作用下，首先发生屈曲变形的互连结构变形较大，而其他互连结构的变形较小，导致结构无法以方形形式展开。在后屈曲变形分析中，通过将集中力改为位移载荷，可使结构以方形形状展开。

B. 2×2阵列不规则岛桥结构

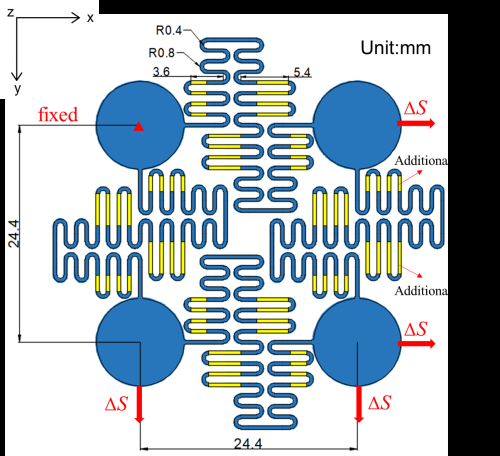
可以看出，分形互连结构对构型所包围的空白区域具有较高的利用率。即便如此，仍可增加局部蛇形互连段的长度l2以优化结构并进一步利用空白区域，如图12所示。然而，优化后的分形互连为不规则结构，其仿真分析更为复杂。

由于优化结构的复杂性，如果使用集中力，仿真容易出现不收敛。因此，仿真采用位移载荷。同样，在屈曲模态分析中，请求的特征值数量设置为40。在后屈曲变形分析中，最大增量步数为2000，初始弧长增量为1E‐7，最小弧长增量为1E‐25，最大弧长增量保持不变。此外，应引入屈曲模式的50%位移值作为初始缺陷。

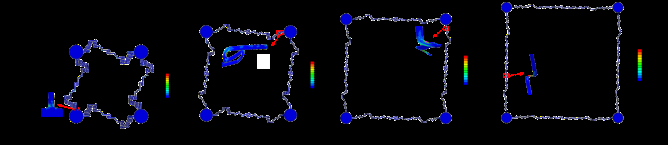
仿真结果如图13所示。当结构拉伸至初始面积的2500%时，最大应变为0.091%。同样，最大应变也位于内弧顶部。优化后，内部应变水平显著降低，拉伸性得到增强。

V. 结论

本文提出了基于ABAQUS的岛‐互连结构网络的仿真方法，可指导可拉伸传感器网络的设计，包括屈曲模态分析和后屈曲变形分析。基于该仿真方法，可分析不同类型岛桥结构网络的屈曲变形和力学性能，包括蛇形、分形和不规则岛桥结构网络。仿真结果表明， 1×3阵列蛇形岛桥结构的拉伸性为95%，而2×3阵列蛇形岛桥结构可拉伸至其初始面积的360%。然而，对称结构中间岛的最大旋转角度仅为1°，而非对称结构的最大旋转角度大于10°。对于方向敏感传感器，不能将其布置在非对称结构上。此外，对于2×2阵列分形岛桥结构，当拉伸至其初始面积的2500%时，结构的最大应变为0.65%，而优化后的不规则结构中，结构的最大应变降低至0.091%，拉伸性进一步增强。综上所述，该仿真方法简单，适用于不同类型岛桥结构网络的屈曲变形分析，可进一步指导和优化大规模传感器网络的设计。然而，随着结构复杂性的增加，仿真计算量将大幅增加，该仿真方法仍需进一步优化以减少计算量。