数据类型介绍
类型的意义
类型的基本分类
整形
void test(void)
{
printf("这里不需要接受参数,也不需要返回,所以都是void\n");
}
int main()
{
test();
return 0;
}有了大致的介绍,我们接下来先介绍整数在内存中的存储。
整形在内存中的存储
这里我之前已经介绍过了,可以到这个里移位操作符的原码,反码,补码这里具体看一下【编程之路(008)操作符详解】(C语言实现)_p_fly的博客-优快云博客
另外需要补充一下,无符号的数可以理解为正数。
如果你已经看完了整数的存储或者你已经知道其存储方法,那么接下来我会补充为什么是这样存储的。
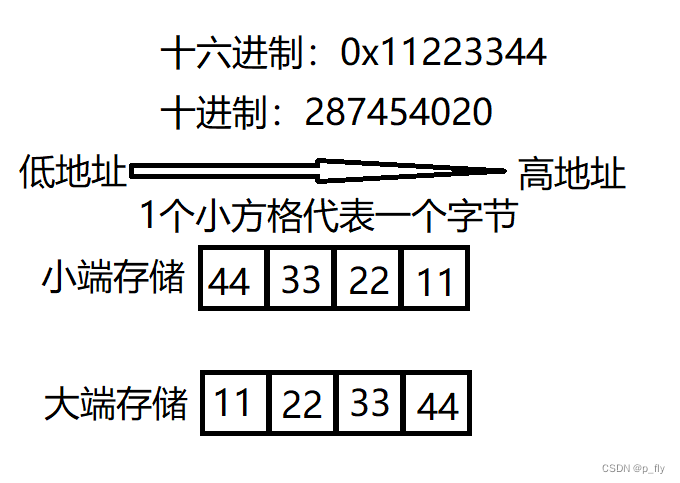
大小端字节序
#include<stdio.h>
int main()
{
int a = 1;
//1的十六进制:0x 00 00 00 01
//把a的地址取出,并且强制转换成char*类型的指针
//强制转换的意义是为了微操:具体看到每一个字节是什么值
char* pa = (char*)&a;
if (*pa == 1)
{
printf("小端\n");
}
else
{
printf("大端\n");
}
return 0;
}总结一下:小端就是老老实实,低位存放到低地址,大端比较叛逆,与之相反。
整形的存储练习
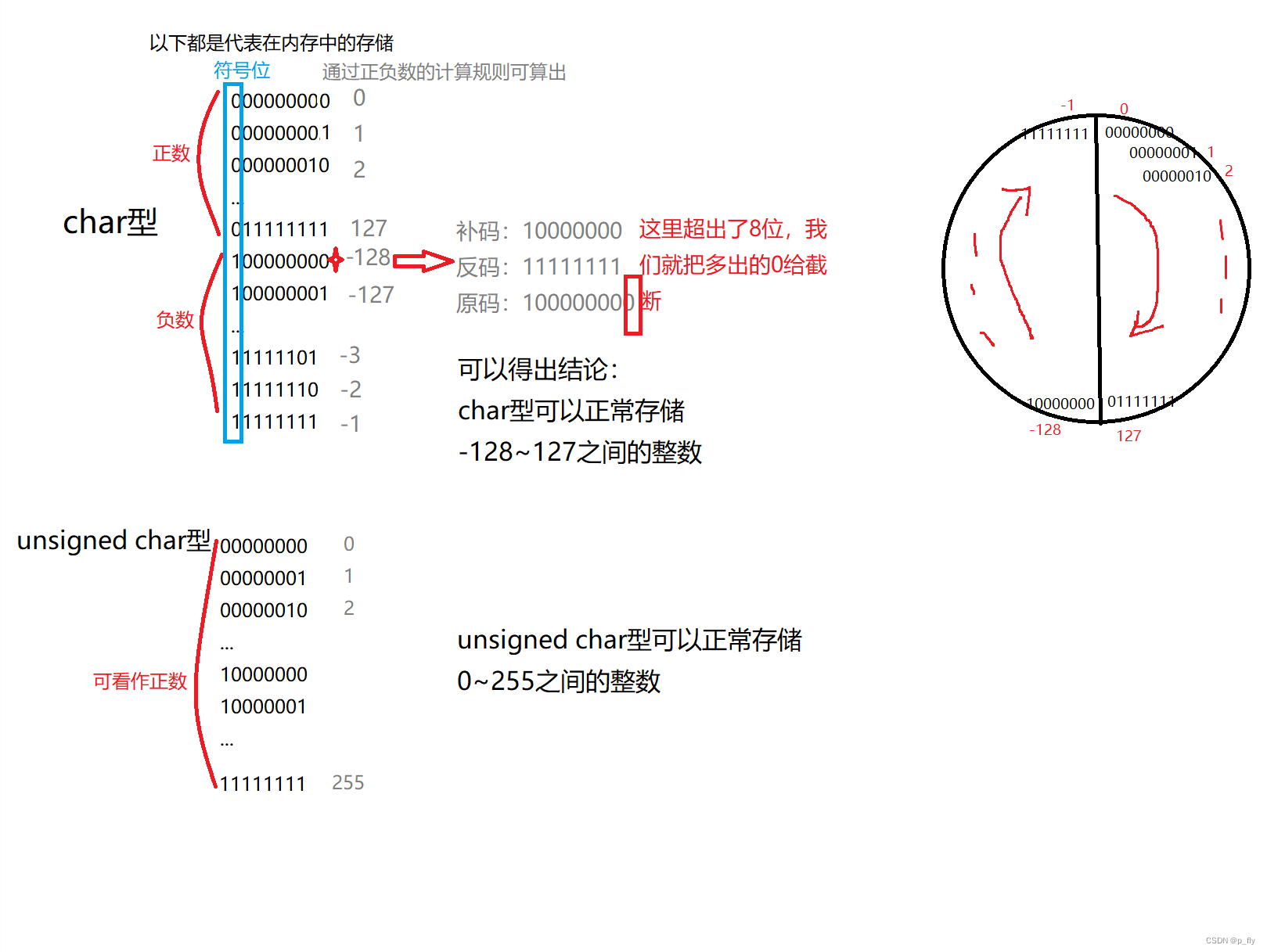
练习之前需要了解
1.
//打印什么?
#include <stdio.h>
int main()
{
char a = -1;
//-1
//原码:10000000 00000000 00000000 00000001
//反码:11111111 11111111 11111111 11111110
//补码:11111111 11111111 11111111 11111111
//因为char类型只能放下一个字节(8个比特位),所以在内存中存储就要截断
//实际:11111111
signed char b = -1;
//vs2019下,char与signed char一样
//实际:11111111
unsigned char c = -1;
//-1
//原码:10000000 00000000 00000000 00000001
//反码:11111111 11111111 11111111 11111110
//补码:11111111 11111111 11111111 11111111
//和上面一样
//实际:11111111
printf("a = %d\nb = %d\nc = %d\n", a, b, c);
//以%d的形式打印--以整形的形式打印
//所以a,b,c都要整形提升才可以打印
//整形提升看类型,类型是有符号的类型,高位补符号位
// 类型是无符号的类型,高位补0
//整形提升:
//a:补码:11111111 11111111 11111111 11111111
// 反码:10000000 00000000 00000000 00000000
// 原码:10000000 00000000 00000000 00000001
//b:与a同理
// 原码:10000000 00000000 00000000 00000001
//c:补码:00000000 00000000 00000000 11111111
//由于c是无符号类型,可以看作正数。正数的原码,反码与补码相同
return 0;
}结果如下: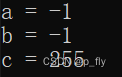
2.
#include <stdio.h>
int main()
{
char a = -128;
//补码:10000000 00000000 00000000 10000000
//实际:10000000(存的后低八位)
printf("%u\n", a);
//打印的是无符号整数
//整形提升,a是char型,有符号,高位补符号位
//补码:00000000 00000000 00000000 10000000
//反码:11111111 11111111 11111111 01111111
//原码:11111111 11111111 11111111 10000000
return 0;
}结果: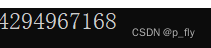
3.
#include <stdio.h>
int main()
{
char a = 128;
//因为是正数,所以补码==反码==原码:
// 00000000 00000000 00000000 10000000
//实际:10000000
printf("%u\n", a);
//整形提升,a为char型,高位补符号位
//11111111 11111111 11111111 10000000
return 0;
}结果:
4.
#include<stdio.h>
int main()
{
int i = -20;
//原码:10000000 00000000 00000000 00010100
//反码:11111111 11111111 11111111 11101011
//补码:11111111 11111111 11111111 11101100
unsigned int j = 10;
//原码==反码==补码:00000000 00000000 00000000 00001010
printf("%d\n", i + j);
//按照补码的形式进行运算,最后格式化成为有符号整数
//补码:11111111 11111111 11111111 11110110
//反码:10000000 00000000 00000000 00001001
//原码:10000000 00000000 00000000 00001010
}
//结果:-105.
#include<stdio.h>
int main()
{
unsigned int i;
for (i = 9; i >= 0; i--)
{
printf("%u\n", i);
}
return 0;
}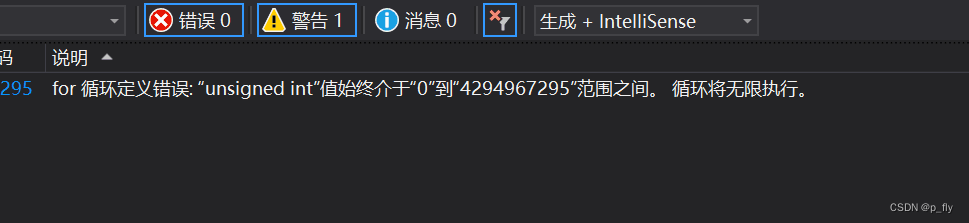
这里程序会陷入死循环,编译器也警告了。就跟第一题之前的那个图中的unsigned char情况一样,就算在这么减,它也还是正数。
6.
#include<stdio.h>
int main()
{
//-128~127
char a[1000];
int i;
for (i = 0; i < 1000; i++)
{
a[i] = -1 - i;
}
//-1 -2 -3 ... 0
//a[0] a[1] a[2]... a[x]
//根据上图的圆环表示,从-1到0之间有127+128=255个
printf("%d", strlen(a));
//strlen是计算字符串个数的,当找到'\0'也就是0时,会停止
return 0;
}
//结果为2557.
#include <stdio.h>
unsigned char i = 0;
int main()
{
for (i = 0; i <= 255; i++)
{
printf("hello world\n");
}
return 0;
}
//结果:死循环打印由于我们知道,unsigned char的范围是0~255,所以就会一直循环。
小结一下:当大的类型的要放到小的类型中时,这时就会发生截断(保留低位)。(主要只是有 放的动作的时候才会截断)。
当要使用被截断的小的类型要拿出来使用时,看是否可以与使用对象相对应(比如 char类型的以%d形式打印的时候,就要发生整形提升)。
整形提升要看原本的类型,原类型是有符号类型,按符号位提升,否则补0;
以上便是整数部分的内容,接下来的部分将会介绍浮点数在内存中的存储。
浮点型在内存中的存储
浮点数存储规则:
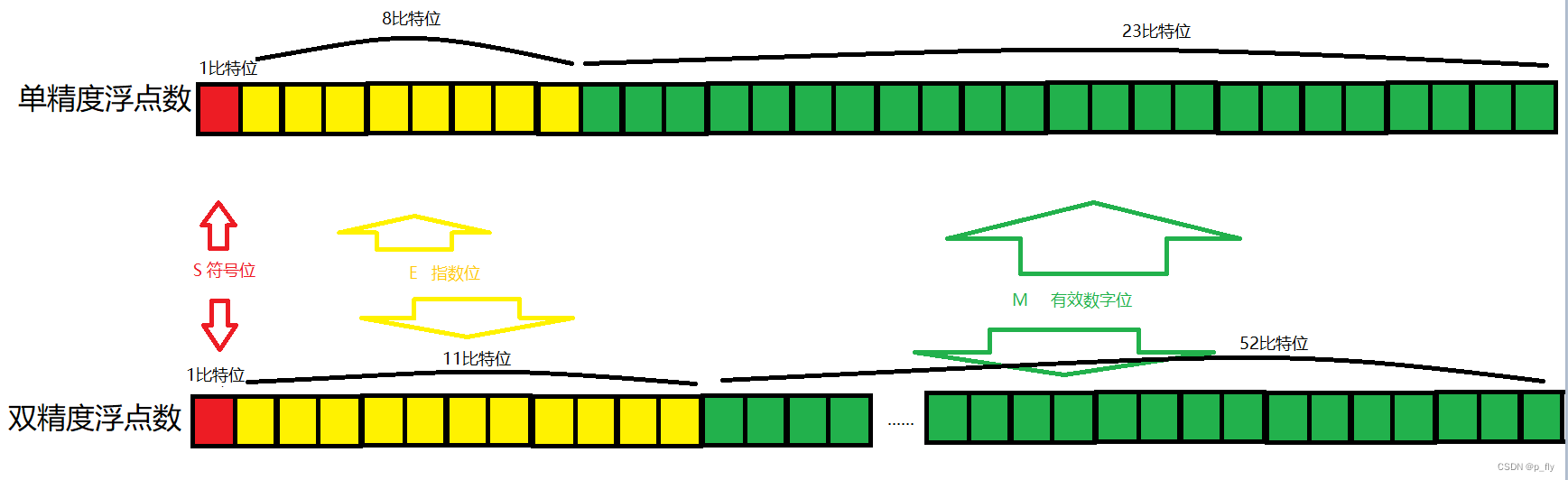
举个简单的例子:
十进制5.0==二进制101.0==1.01×2^2(这里可以类比成十进制的科学计数法)
希望这篇文章可以帮到你,有什么不对的也希望在评论区提出来。





 本文详细介绍了C语言中的数据类型,包括整型、浮点型、构造型和指针类型,以及它们在内存中的存储方式。重点讨论了整数的原码、反码、补码表示,大小端字节序的概念,以及如何通过代码判断系统字节序。还探讨了浮点数在内存中的IEEE 754标准表示。
本文详细介绍了C语言中的数据类型,包括整型、浮点型、构造型和指针类型,以及它们在内存中的存储方式。重点讨论了整数的原码、反码、补码表示,大小端字节序的概念,以及如何通过代码判断系统字节序。还探讨了浮点数在内存中的IEEE 754标准表示。
















 876
876

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








