【实例分享】基于粒子群算法优化的PID参数调整方案：详解MATLAB代码，注释详细，利用PSO算法对Kp、Ki和Kd系数进行寻优，以ITAE指标为适应度函数，使用粒子群算法优化PID参数：基于MATL

matlab代码：基于粒子群算法的PID参数优化
-注释详细
-利用PSO算法对Kp、Ki和Kd三个系数的寻优
-选择ITAE指标作为适应度函数

ID:2712673428028725

路卡利欧呀

粒子群算法（Particle Swarm Optimization，PSO）是一种基于群体智能的优化算法，它模拟了鸟群觅食的行为方式。PSO算法通过自适应的方式在搜索空间中寻找最优解，特别适用于复杂非线性问题的优化。在控制系统中，PID控制器是一种常用且有效的控制算法，但PID参数的选择对控制系统的性能具有重要影响。本文将采用PSO算法对PID控制器的参数进行优化，以提高控制系统的性能。

首先，我们需要对matlab代码中的注释进行详细的解读。注释是代码中的文字说明，对于理解代码的功能和实现方式非常重要。详细的注释可以帮助其他开发者更好地理解代码，从而更快地进行代码调试和修改。

在PSO算法中，粒子代表了一个潜在的解，粒子的位置表示了解的位置，粒子的速度表示了解的搜索方向和速度。粒子群中的每个粒子通过与自身历史最优位置和整个群体历史最优位置进行比较，来更新自身的位置和速度。通过不断迭代更新，PSO算法可以找到最优解。

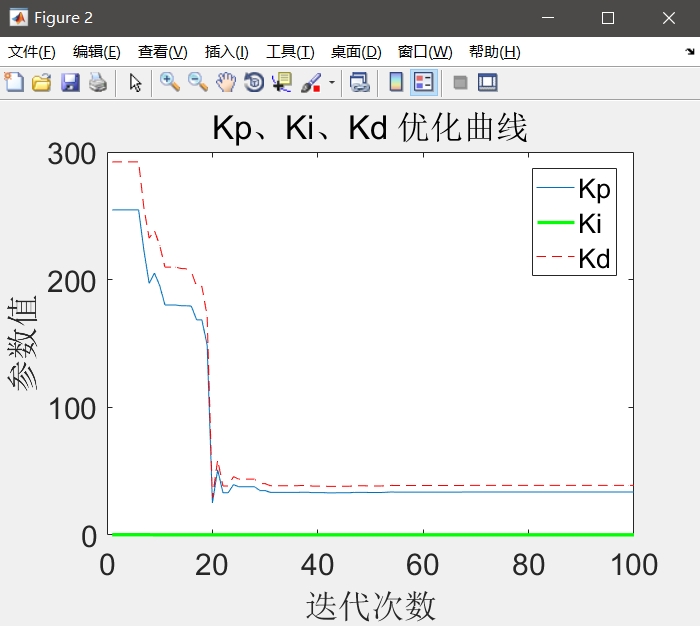
在PID控制器中，Kp、Ki和Kd分别代表比例、积分和微分参数。这三个参数的选择直接影响着控制系统的性能。传统的参数选择方法往往需要依赖经验和试错，效率较低。通过利用PSO算法对这三个参数进行优化，可以快速获取到最优的控制参数。

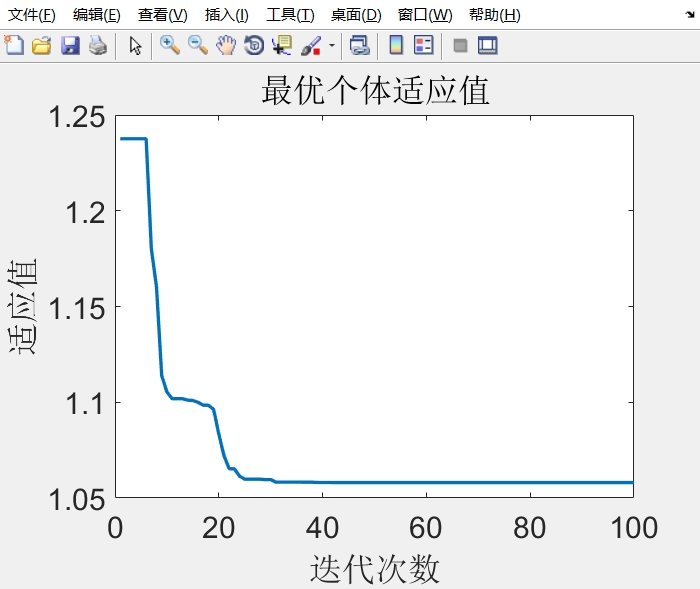
为了评估PID控制器的性能，我们选择了ITAE指标作为适应度函数。ITAE指标（Integral of Time multiplied by the Absolute value of Error）综合考虑了控制系统的稳态误差和响应时间，能够客观反映出控制系统的性能。通过优化ITAE指标，我们可以得到更好的控制效果。

在使用PSO算法进行PID参数优化时，首先需要设置好PSO算法的参数。例如，设定群体规模、迭代次数、惯性权重等参数。然后，根据需要优化的问题，确定变量范围和粒子的初始位置和速度。在每次迭代中，根据粒子的适应度函数值，更新粒子的位置和速度。通过不断迭代更新，粒子逐渐接近最优解，从而找到最优的PID参数。

在进行实际优化之前，应该先对PSO算法进行验证和测试。可以通过构造一些简单的函数来测试算法的性能，比如二维函数的极小值问题。通过不断调整PSO算法的参数和设置，找到使得算法收敛快速、找到最优解的最佳参数配置。

在得到最优的PID参数后，可以将其应用于实际的控制系统中。通过观察和分析控制系统的响应曲线、稳态误差和控制效果，评估PID参数的优化结果。如果需要进一步优化，可以通过修改PSO算法的参数或者调整适应度函数来获取更好的结果。

综上所述，本文介绍了基于粒子群算法的PID参数优化方法。通过利用PSO算法对Kp、Ki和Kd三个系数进行优化，选择ITAE指标作为适应度函数，可以有效提高控制系统的性能。通过详细的注释和实验验证，我们展示了该方法的有效性和可行性。希望本文能够为读者提供有价值的参考，并促进PID参数优化的研究和实践。

相关的代码,程序地址如下：http://wekup.cn/673428028725.html