ACM算法题第七周

第一题：

机器猫被困在一个矩形迷宫里。

迷宫可以视为一个 n×m 矩阵，每个位置要么是空地，要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。

机器猫初始时位于 (1,1) 的位置，问能否走到 (n,m) 位置。

输入格式

第一行，两个正整数 n,m。

接下来 nn 行，输入这个迷宫。每行输入一个长为 m 的字符串，# 表示墙，. 表示空地。

输出格式

仅一行，一个字符串。如果机器猫能走到 (n,m)，则输出 Yes；否则输出 No。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m;
char a[105][105];
bool escape;
int dx[4]={0,1,-1,0};
int dy[4]={1,0,0,-1};
void dfs(int x,int y){
    if(x<1||x>n||y<1||y>m) return;
    if(x==n&&y==m) escape=1;
    if(escape) return; 
    for(int i=0;i<4;i++){
        if(a[x+dx[i]][y+dy[i]]!='#'){
            a[x+dx[i]][y+dy[i]]='#';
            dfs(x+dx[i],y+dy[i]);
        }
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    a[1][1]='#';
    dfs(1,1);
    if(escape==1) cout<<"Yes";
    else cout<<"No";
    return 0;
} 

解题思路：

        本题新定义dx、dy数组用于表示移动方向，然后从（1，1）开始，如果移动后符合条件且未遇到障碍，那么从这个点开始下一次移动，并把这个点标记为障碍。依次搜索下去，如果越界则结束，如果恰好走到终点，就把escape赋值为1然后结束

第二题：

按照字典序输出自然数 1 到 n 所有不重复的排列，即 n 的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入格式

一个整数 n。

输出格式

由 1∼n 组成的所有不重复的数字序列，每行一个序列。

每个数字保留 5 个场宽。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,a[10],b[10];
void dfs(int step){
    if(step==n+1){
        for(int i=1;i<=n;i++){
            printf("%5d",a[i]);
        }
        cout<<endl;
        return;
    }
        for(int i=1;i<=n;i++){
            if(b[i]==0){
                a[step]=i;
                b[i]=1;
             dfs(step+1);
            b[i]=0;
            }
        }
}
int main(){
    cin>>n;
    dfs(1);
    return 0;
}

解题思路：

定义a，b两个数组一个用来表示全排列，一个用来记录数字是否使用过。dfs函数中，先判断step即存放的数字数目是否到达n+1，如果到达则输出数组a，并返回上一个dfs；如果没达到，那么从1开始遍历，遇到第一个未使用的数就存放进a数组，然后进行下一位的数字存放，并进入下一个dfs，当全部遍历后，函数结束。

第三题：

一矩形阵列由数字 0 到 9 组成，数字 1 到 9 代表细胞，细胞的定义为沿细胞数字上下左右若还是细胞数字则为同一细胞，求给定矩形阵列的细胞个数。

输入格式

第一行两个整数代表矩阵大小 n 和 m。

接下来 nn 行，每行一个长度为 m 的只含字符 0 到 9 的字符串，代表这个 n×m 的矩阵。

输出格式

一行一个整数代表细胞个数。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,m,cnt;
int a[105][105];
int dx[4]={1,0,0,-1};
int dy[4]={0,1,-1,0};
void dfs(int x,int y){
    a[x][y]=0;
    for(int i=0;i<4;i++){
        x+=dx[i];
        y+=dy[i];
        if(x>0&&x<=n&&y>0&&y<=m&&a[x][y]!=0){
            dfs(x,y);
        }
        x-=dx[i];
        y-=dy[i];
    }
}
int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            scanf("%1d",&a[i][j]);
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]==0) continue;
            dfs(i,j);
            cnt++;
        }
    }
    cout<<cnt;
    return 0;
}

解题思路：

设置dx、dy两个数组表示四个移动方向，然后开始遍历每个点，如果该点数据为0，则跳过；如果不是，那么进入dfs函数。dfs函数中，遍历dx、dy四个方向，如果四个方向中仍有非零的，那么就赋值为零，直到把这一整块相连的非零都赋值为零，然后计数并搜索下一块。

第四题：

一个如下的 6×6 的跳棋棋盘，有六个棋子被放置在棋盘上，使得每行、每列有且只有一个，每条对角线（包括两条主对角线的所有平行线）上至多有一个棋子。

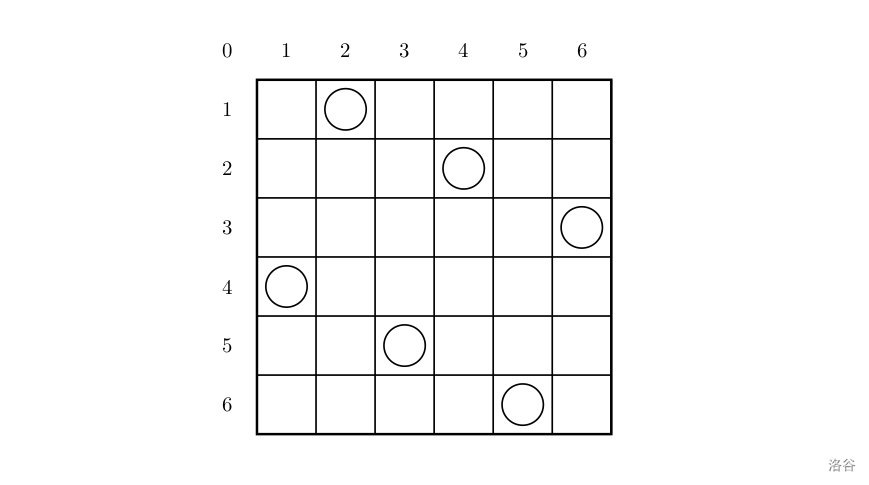
上面的布局可以用序列 2 4 6 1 3 5 来描述，第 i 个数字表示在第 i 行的相应位置有一个棋子，如下：

行号 1 2 3 4 5 6

列号 2 4 6 1 3 5

这只是棋子放置的一个解。请编一个程序找出所有棋子放置的解。
并把它们以上面的序列方法输出，解按字典顺序排列。
请输出前 3 个解。最后一行是解的总个数。

输入格式

一行一个正整数 n，表示棋盘是 n×n 大小的。

输出格式

前三行为前三个解，每个解的两个数字之间用一个空格隔开。第四行只有一个数字，表示解的总数。

代码：

#include<bits/stdc++.h>
using namespace std;
int n,ans;
int a[30],b[30],c[30],d[30];
void print(){
    if(ans<=2){
        for(int i=1;i<=n;i++){
            cout<<a[i]<<' ';
        }
        cout<<endl;
    }
    ans++;
}
void queen(int i){
    if(i==n+1){
        print();
        return;
    }else{
        for(int j=1;j<=n;j++){
            if((b[j]==0)&&(c[i+j]==0)&&(d[i-j+n]==0)){
                a[i]=j;
                b[j]=1;
                c[i+j]=1;
                d[i-j+n]=1;
                queen(i+1);
                b[j]=0;
                c[i+j]=0;
                d[i-j+n]=0;
                
            }
        }
    }
}
int main(){
    cin>>n;
    queen(1);
    cout<<ans;
    return 0;
}

解题思路：

需要设置三个数组来储存列以及两个对角线的占据情况，然后开始一次尝试可能的位置，如果皇后没有占领，执行占据并搜索下一个皇后位置，如果不行就回到上一个皇后的位置。此处输入是需要对总方案数做一个判断，输出前三个方案，但是每一次达到n+1后，方案数都加1.