动态规划学习笔记&解题思路

动态规划基本思路：正向思考，逆向计算，推出状态转移方程；

解题方法：1.根据题目定义一个数组，并明确数组的含义。

                  2.根据题目找出数组各个元素间的关系，并写出表达式

                  3.根据题干求出表达式表达范围之外的初始值

补充：二维数组的dp问题：

        例子：有一个机器人位于一个 m x n 网格的左上角 （起始点在下图中标记为“Start” ）。

机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角（在下图中标记为“Finish”）。

问总共有多少条不同的路径？

思路：根据机器人只能向下或向右走，因此构建一个二维数组a[m][n]，机器人起点为（1，1），其中a[i][j]只能由a[i-1][j]或者a[i][j-1]到达.

        因此可以得到状态转移方程，之后再考虑边上的特殊情况，因为边上只能有一种到达方式，因此到达对应点的方式只有一种，初始值全部设为一，其余点都设为0，然后通过循环计算得到a[m][n]的值即为路径总数。

优化方法：因为在计算第i行时，我们只会用到i-1行的数据，所以可以只构建一个一维数组保存前一行的值即可，后续计算中逐个覆盖即可。

例题：

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

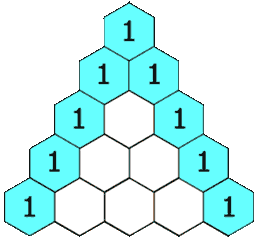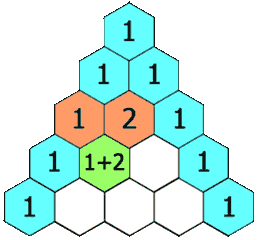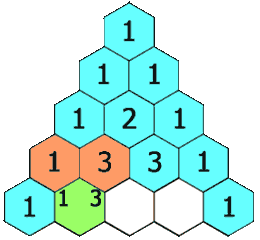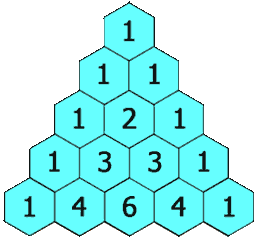
示例 1:

输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:

输入: numRows = 1
输出: [[1]]

代码：#include<bits/stdc++.h>
using namespace std;
int n;
int a[30][30];
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
            a[i][1]=1;
            a[i][i]=1;
    }
    for(int i=3;i<=n;i++){
        for(int j=i-1;j>1;j--){
            a[i][j]=a[i-1][j-1]+a[i-1][j];
        }
    }
    cout<<'[';
    if(n==1){
            printf("[%d]",a[1][1]);
                cout<<']';
            return 0;
        }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            if(i==1&&j==1) printf("[%d],",a[i][j]);
            else if(i!=1&&j==1) printf("[%d",a[i][j]);
            else if(i!=1&&i!=n&&j==i) printf(",%d],",a[i][j]);
            else if(i==n&&j==i) printf(",%d]",a[i][j]);
            else printf(",%d",a[i][j]);
        }
    }
    cout<<']';
    return 0;
}

第二题：

给定一个三角形 triangle ，找出自顶向下的最小路径和。

每一步只能移动到下一行中相邻的结点上。相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。也就是说，如果正位于当前行的下标 i ，那么下一步可以移动到下一行的下标 i 或 i + 1 。

   2
  3 4
 6 5 7
4 1 8 3
自顶向下的最小路径和为 11（即，2 + 3 + 5 + 1 = 11）。

代码：#include<bits/stdc++.h>
using namespace std;
int n,a[1005][1005];
int main(){
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++){
            cin>>a[i][j];
        }
    }
    for(int i=n-1;i>=1;i--){
        for(int j=1;j<=i;j++){
            a[i][j]+=min(a[i+1][j],a[i+1][j+1]);
        }
    }
    cout<<a[1][1];
    return 0;
}

思路：从倒数第二行开始，用这一行与最后一行向临的两个数求出最小值，然后一次向上计算，最后第一行第一列的数据即为最小值。