函数的特殊形式——递归_递归寻宝-优快云博客

一、故事引入：递归寻宝的黑龙传说

黑龙阿尔法为了装饰龙窟需要收集16颗能量宝石，展开了一场充满递归智慧的寻宝之旅：

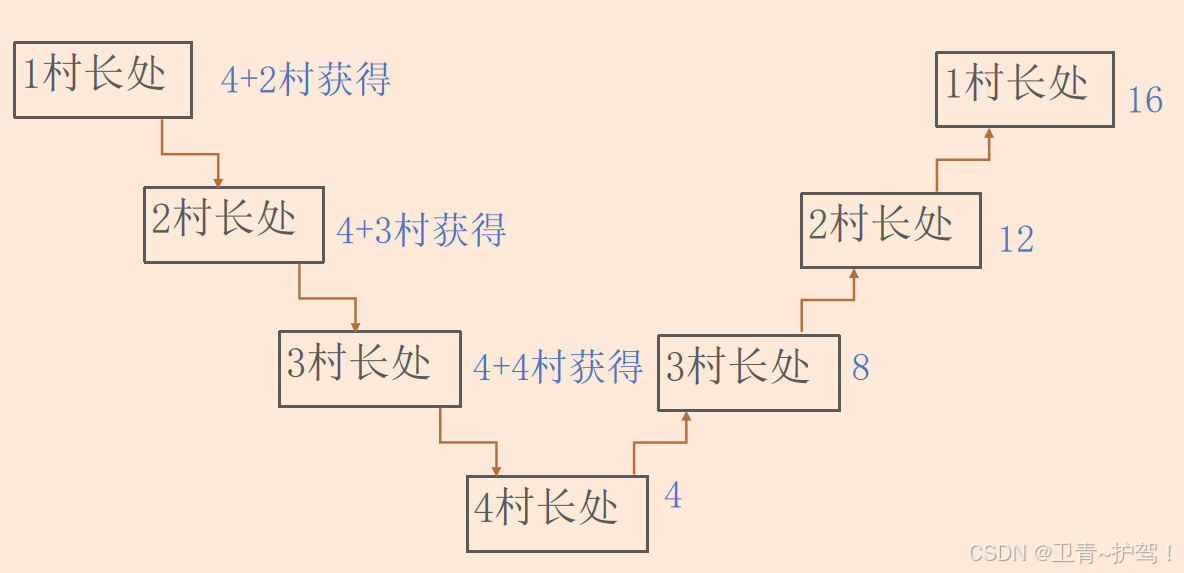
阿尔法来到1号村庄，村长提出交易条件："若你能从2号村带回12颗宝石，我将赠你4颗"。黑龙展翅飞向2号村，却发现新的挑战——2号村长要求它从3号村获得8颗宝石来换取4颗馈赠。当来到3号村时，故事再次重演：需要先前往4号村获取4颗宝石。

在旅途终点的4号村，阿尔法终于直接获得了4颗宝石。带着这份收获：

在4号村：得到4颗
返回3号村：4颗(自带)+4颗(馈赠)=8颗
回到2号村：8颗(自带)+4颗=12颗
回到1号村：12颗(自带)+4颗=16颗

这场宝石收集之旅完美演绎了递归算法的核心要素：
🏮 递归条件：每个村庄的宝石需求以4颗递减（16→12→8→4）
🎯 基准情形：4号村直接满足最小规模需求
🔄 回溯过程：逐层返回时累加计算结果

每个村庄的交易规则"带回n-4颗即赠4颗"，正是递归思想的生动写照——将复杂问题（收集16颗）分解为相同类型的子问题（收集12颗），直到遇到可直接解决的最小问题（收集4颗）。

二、递归函数原理剖析

1.过程分析

黑龙阿尔法在四个村庄的宝石收集过程，完美呈现了递归算法的核心机制：

初始调用：1号村请求16颗宝石（findGem(16)）
递归展开：逐层调用findGem(12)→findGem(8)→findGem(4)
基准情形：4号村直接返回4颗（终止条件达成）
回溯计算：3号村(4+4)→2号村(8+4)→1号村(12+4)

2. 递归三要素对照表

递归要素	黑龙案例映射	代码对应
终止条件	4号村直接提供宝石	`if(target == 4)`
递归调用	向下一级村庄寻求帮助	`findGem(target - 4)`
问题简化	宝石需求每次递减4颗	`target - 4`

三、递归函数核心语法结构

1. 标准模板

返回类型 函数名(参数列表) {
    if(终止条件成立) {
        return 基准解;
    }
    return 递归操作(简化参数);
}

2. 黑龙案例实现

int findGem(int target) {
    // 终止条件：最小规模问题
    if(target == 4) { 
        cout << "到达4号村，获得4颗宝石" << endl;
        return 4;
    }
    
    // 递归调用：解决子问题
    int sub_gem = findGem(target - 4);
    
    // 结果处理：当前层逻辑
    cout << "在目标" << target << "的村庄，获得4颗宝石" << endl;
    return sub_gem + 4;
}