本文详细介绍了深度学习中的常见指标，如IOU，以及转置卷积的概念，指出其在图像尺寸恢复中的作用，并通过实例解释了转置卷积的过程。接着讨论了感受野的概念及其在特征层下采样中的影响。最后，探讨了膨胀卷积，说明其如何增加感受野并保持图像尺寸不变，以及在需要全局信息时的应用。膨胀卷积通过调整膨胀系数来平衡信息保留与计算效率。
目录
常见指标
IOU：交集除以并集
转置卷积
转置卷积也叫反卷积，其本质就是卷积。在深度学习中表示为卷积的一个逆向过程，可以根据卷积核大小和输出的大小，恢复卷积前的图像尺寸，而不是恢复原始值。
正常卷积运算的不同方式，将每次滑动的卷积核都扩充为一个新的与输入的特征层相同大小的数组矩阵。
然后讲特征层横向展平，变为一个1*16的矩阵，然后将扩充过大小的矩阵列向展平合并，变为一个16*4的矩阵，相乘变为1*4的矩阵。
所以当我们想要尝试在已知C（16*4）与O（1*4）时是否能得出I（1*16），即C矩阵是否可逆。矩阵可逆的前提是方阵，C不是，故不可逆。 但当我们放宽条件，将还原I矩阵变为，还原出与I矩阵大小相同的矩阵那就简单多了，可以直接将C转置,再乘以O矩阵.
可以将其理解为将转置的卷积拆成16个4*4卷积核，并分别卷积。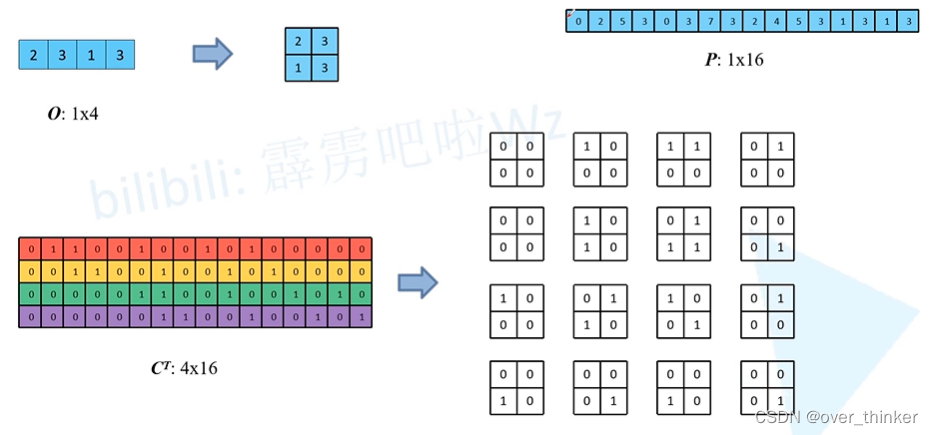
这个时候可以发现，它相当于四周填充0后做的卷积操作。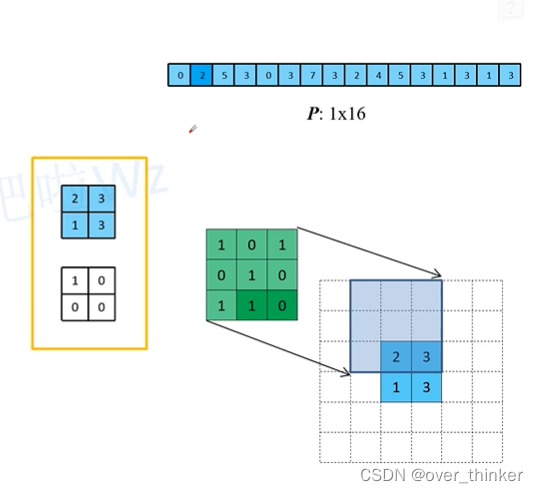
所以转置卷积也是卷积，目标是还原大小。
感受野
如图所示，一个普通的特征层下采样操作， 通过图例可以感受到，在2*2中一个格子，对应的感受野是2*2，对于4*4中，这4个格子对应感受野是5*5.计算公式如下：
用来辅助网络设计。
膨胀卷积
与普通卷积相似，只是增加了扩张率的参数，为了表示膨胀的大小。与普通卷积不同的是增加了感受野。在图像需要全局信息、语音文本需要较长的sequence信息依赖的问题中，可以很好的运用。
这膨胀卷积不是 在原特征图中加入0，而是跳过一些元素，并在卷积核中插入0，使得图像面积不变，则不会因为图像尺寸减小而导致丢失信息。
但是如果直接叠加膨胀卷积，那么会导致感受野中不是所有元素参与到了计算，必然会丢失信息。
改变膨胀系数使得利用的元素更多。
设计膨胀卷积的思路：
目标是使元素之间间隔为0，即M=1.
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
