字典树(Trie)

介绍

• 在计算机科学中，Trie又称前缀树或字典树
• 是一种针对字符串进行维护的非常高效的数据结构
• 最大优点是利用字符串的公共前缀来减少存储空间与查询时间
• 应用于统计、排序和保存大量的字符串（但不仅限于字符串）

例如有 abcd ab abce caa caad 五个字符串，构建字典树如下：

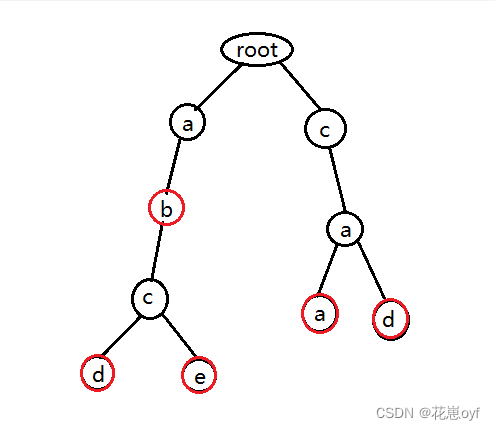
其中红色表示到当前节点时读取到了一个已存在的字符串
字典树有两种基本操作分别是建树和查询

• 建树：把一个目标加入到字典树里
• 查询：查询给定目标在字典树上的属性（是否存在、数量等等）

建树（插入）

假如目标是字符串，且只有小写字母，那么这个树的深度会由字符串而定，广度最大为26
可以开二维数组 trie[N][26] 代表节点，每个节点的值为下一个节点的位置，然后通过深度迭代向里面尝试加入字符串
用 ind 表示已经使用的最后一个节点，cnt[i] 表示第 i 个节点储存目标的数量
那么插入代码：

void add(string &a){
    int p=0;
    for(int i=0;a[i];i++){
        int t=a[i]-'a';
        if(!trie[p][t])trie[p][t]=++ind;
        p=trie[p][t];
    }
    cnt[p]++;
}

查询

查询操作和插入操作的类似，在字典树根节点按深度向下迭代，对于需要查询的字符串的当前字符，如果这个节点的下一个节点为空，就说明不含这个单词，直接跳出即可
当迭代完成之后，返回 cnt[p]
注意，如果不是求数量而是求目标存不存在，不能直接返回，假如字典中保存了一个字符串 huzai ，而查询的是 hua ，它可以迭代到最后，但是它并不是字典中的字符串，即，需要考虑字典中字符串子串的情况
查询代码：

int query(string &a){
    int p=0;
    for(int i=0;a[i];i++){
        int t=a[i]-'a';
        if(!trie[p][t])return 0;
        p=trie[p][t];
    }
    return cnt[p];
}

经典例题

Trie字符串统计

题目描述

维护一个字符串集合，支持两种操作：

I x 向集合中插入一个字符串 xx；
Q x 询问一个字符串在集合中出现了多少次。

共有 N 个操作，输入的字符串总长度不超过 1e5，字符串仅包含小写英文字母。

输入格式

第一行包含整数 N，表示操作数。
接下来 N 行，每行包含一个操作指令，指令为 I x 或 Q x 中的一种。

输出格式

对于每个询问指令 Q x，都要输出一个整数作为结果，表示 xx 在集合中出现的次数。
每个结果占一行。数据范围1≤N≤2e4

样例

输入

5
I abc
Q abc
Q ab
I ab
Q ab

输出

1
0
1

解题代码

#include<iostream>
using namespace std;
const int N=1e6+7;

int n;
int trie[N][26],cnt[N],ind;

void add(string &a){
	int p=0;
	for(int i=0;a[i];i++){
		int t=a[i]-'a';
		if(!trie[p][t])trie[p][t]=++ind;
		p=trie[p][t];
	}
	cnt[p]++;
}
int query(string &a){
	int p=0;
	for(int i=0;a[i];i++){
		int t=a[i]-'a';
		if(!trie[p][t])return 0;
		p=trie[p][t];
	}
	return cnt[p];
}
int main(){
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	cin>>n;
	string op,s;
	while(n--){
		cin>>op>>s;
		if(op=="I")add(s);
		else cout<<query(s)<<endl;;
	}
	return 0;
}