残差网络ResNet

1. 什么是残差

假设我们想要找一个 $x$，使得$f(x)=b$，给定一个 $x$ 的估计值$x_0$ ，残差（residual）就是 $b-f(x_0)$，同时，误差就是 $x-x_0$；即使 $x$ 不知道，我们仍然可以计算残差，只是不能计算误差罢了

2. 什么是残差网络

2.1 神经网络越深越好吗？

理论上，越深的网络，效果应该更好；但实际上，由于训练难度，过深的网络会产生退化问题，效果反而不如相对较浅的网络。

注意:
过拟合问题是训练集上效果很好，测试集上效果并没有训练集上的好，甚至效果很差
退化问题是在训练集上就效果不好（网络深的训练集效果还没网络浅的效果）随着网络层数增加，在训练集上的准确率却饱和甚至下降了

2.2 残差网络

残差网络通过加入 shortcut connections，变得更加容易被优化。包含一个 shortcut connection 的几层网络被称为一个残差块（residual block），如图 所示。（shortcut connection，即右侧从 x 到 ⨁ 的箭头）

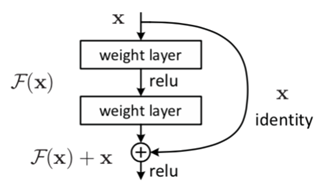
$x$ 表示输入，$F(x)$ 表示残差块在第二层激活函数之前的输出，即$F(x)=W2\sigma (W_{1}x)$，其中 W1 和 W2 表示第一层和第二层的权重，σ 表示 ReLU 激活函数。（这里省略了 bias。）最后残差块的输出是 $\sigma (F(x)+x)$

3.残差网络的作用

随着网络深度的增加，带来了许多问题，梯度消散，梯度爆炸；BN层，Relu等各种激活函数等改善问题的能力有限，直到残差连接被广泛使用；

假如我们有以下问题:
$$\begin{array}{c}{f}^{\prime }=f\left(\mathbf{x},{\mathbf{w}}_{\mathbf{f}}\right)\\ g^{\prime }=g\left(f^{\prime }\right)\\ y^{\prime }=k\left(g^{\prime }\right)\\ \mathrm{cost}=\mathrm{criterion}\left(y,y^{\prime }\right)\end{array}$$
则cost对f的导数为:
$$\frac{d\left(f^{\prime }\right)}{d\left({\mathbf{w}}_{\mathbf{f}}\right)}\times \frac{d\left(g^{\prime }\right)}{d\left(f^{\prime }\right)}\times \frac{d\left(y^{\prime }\right)}{d\left(g^{\prime }\right)}\times \frac{d(\cos t)}{y^{\prime }}$$
一旦其中某一个导数很小，多次连乘后梯度可能越来越小，这就是常说的梯度消散，对于深层网络，传到浅层几乎就没了。但是如果使用了残差，每一个导数就加上了一个恒等项1，$dh/dx=d(f+x)/dx=1+df/dx$。此时就算原来的导数$df/dx$很小，这时候误差仍然能够有效的反向传播，这就是核心思想

神经网络的退化才是难以训练深层网络根本原因所在，而不是梯度消散。虽然梯度范数大，但是如果网络的可用自由度对这些范数的贡献非常不均衡，也就是每个层中只有少量的隐藏单元对不同的输入改变它们的激活值，而大部分隐藏单元对不同的输入都是相同的反应，此时整个权重矩阵的秩不高。并且随着网络层数的增加，连乘后使得整个秩变的更低，这也是我们常说的网络退化问题，虽然是一个很高维的矩阵，但是大部分维度却没有信息，表达能力没有看起来那么强大；残差连接正是强制打破了网络的对称性，提升了网络的表征能力。