本文介绍了最大流相关概念，包括源点、汇点、容量、流量等，阐述了最大流问题中容量和流量需满足的三个性质。还讲解了增广路算法，基于残量网络找增广路来增加流量，指出残量网中无增广路时当前流为最大流。最后给出hdu 3549最大流增广路入门模板题及最大流模板。
转载于：https://blog.youkuaiyun.com/freezhanacmore/article/details/9366053
查看资料：lrj 《算法竞赛入门经典》
相关概念：
最大流：（Maximum-Flow Problem）
从源点 S 中间经过一些点，一些的物品运送到汇点 t 。
中途每两点间都有个最大运送物品数。
求从 s 到 t 最多能运送多少物品。
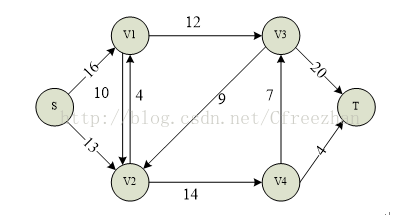
容量： 对于一条边 (u,v),它的物品上限（能够运送的物品最大数量）称为容量 （capacity），
记为 c(u,v) (对于不存在的边 (u,v) , c(u,v) = 0)
流量： 实际运送物品数称为流量 （flow）
规定：f(u,v) 和 f(v,u) 最多只有一个正数（可以均为 0），且 f(u,v) = - f(v,u)
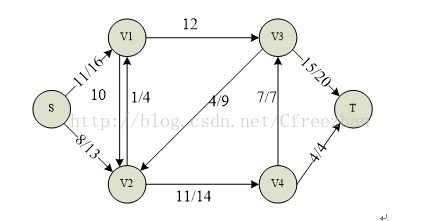
PS：此图左边表示实际运送物品，右边表示最大容量。
结论：对于除了 s 和 t 的任意节点 u, ∑ f(u,v) = 0 (有些 f 为负数) 。
(u,v)∈E
最大流问题中： 容量 c 和 流量 f 满足三个性质
容量限制 f(u,v) <= c(u,v)
斜对称：f(u, v) = -f(u,v)
流量平衡：对于除了 s 和 t 的任意节点 u, ∑ f(u,v) = 0 (有些 f 为负数) 。
(u,v)∈E
目标：最大化 | f | = ∑ f(s,v) = ∑ f(u,t) 即从 S 点流出的净流量（=流入 t 点的净流量）
(s,v)∈E , (u,t)∈E
增广路算法：
残量：上图中每条边上的容量差 （称为残余流量，简称残量），
比如说上面第二个图中 V2 到 V4 残量为 14-11 = 3; V4 到 V2 残量为 0-（-11）= 11
算法基于事实：
残量网络中任何一个从 s 到 t 的有向道路都对应一条原图中的增广路【PS：不理解这个名词也没事继续看】。
只要求出该道路中所有残量的最小值 d,把对应的所有边上的流量增加 d 即可，这个过程称为增广。
也就是说只要有从起点 s 到终点 t 的路上存在流量，那么找出最小的残余流量 d
那么这个 d 肯定是满足这条路径的每一条边的，否则找不出这样的 d
那么这条路径上的每一条边的流量增加 d ，总流量增加 d 就好了。
然后继续找，直到找不到为止。
不难证明如果增广前的流量满足 3 个条件，那么增广之后任然满足。
显然只要残量网中存在增广路，流量就可以增大。
逆命题：如果残量网中不存在增广路，则当前流就是最大流，这就是著名的增广路定理。
问题：如何找路径？ DFS ms 很慢，用 BFS
-
queue<
int> q;
-
memset(flow,
0,
sizeof(flow));
//初始化流量为 0
-
f =
0;
// 初始化总流量为 0
-
for(;;)
//BFS 找增广路
-
{
-
memset(a,
0,
sizeof(a));
// a[i]:从起点 s 到 i 的最小残量【每次for()时 a[] 重新清 0 因此同时可做标记数组 vis】
-
a[s] = INF;
//起点残量无线大
-
q.push(s);
//起点入队
-
while(!q.empty())
// BFS 找增广路
-
{
-
int u = q.front();
//取队首
-
q.pop();
// 出队
-
for(
int v =
1; v <= n; v++)
if(!a[v] && cap[u][v] > flow[u][v])
//找新节点 v
-
{
-
p[v] = u; q.push(v);
//记录 v 的父亲节点,并加入 FIFO 队列
-
a[v] = min(a[u], cap[u][v]-flow[u][v]);
// s-v 路径上的最小残量【从而保证了最后,每条路都满足a[t]】
-
}
-
}
-
-
if(a[t] ==
0)
break;
// 找不到，则当前流已经是最大流 【t为终点】
-
-
for(
int u = t; u != s; u = p[u])
// 从汇点往回走
-
{
-
flow[p[u]][u] += a[t];
// 更新正向流
-
flow[u][p[u]] -= a[t];
// 更新反向流
-
}
-
f += a[t];
// 更新从 S 流出的总流量
-
}
推荐入门题目：
hdu 3549 Flow Problem【最大流增广路入门模板题】
另外下面copy了下KB神给的最大流模板：
暂时没有看懂Orz
最大流模板：
-
const
int MAXN=
20010;
//点数的最大值
-
const
int MAXM=
880010;
//边数的最大值
-
const
int INF=
0x3f3f3f3f;
-
-
struct Node
-
{
-
int from,to,next;
-
int cap;
-
}edge[MAXM];
-
int tol;
-
int head[MAXN];
-
int dep[MAXN];
-
int gap[MAXN];
//gap[x]=y :说明残留网络中dep[i]==x的个数为y
-
-
int n;
//n是总的点的个数，包括源点和汇点
-
-
void init()
-
{
-
tol=
0;
-
memset(head,
-1,
sizeof(head));
-
}
-
-
void addedge(int u,int v,int w)
-
{
-
edge[tol].from=u;
-
edge[tol].to=v;
-
edge[tol].cap=w;
-
edge[tol].next=head[u];
-
head[u]=tol++;
-
edge[tol].from=v;
-
edge[tol].to=u;
-
edge[tol].cap=
0;
-
edge[tol].next=head[v];
-
head[v]=tol++;
-
}
-
void BFS(int start,int end)
-
{
-
memset(dep,
-1,
sizeof(dep));
-
memset(gap,
0,
sizeof(gap));
-
gap[
0]=
1;
-
int que[MAXN];
-
int front,rear;
-
front=rear=
0;
-
dep[end]=
0;
-
que[rear++]=end;
-
while(front!=rear)
-
{
-
int u=que[front++];
-
if(front==MAXN)front=
0;
-
for(
int i=head[u];i!=
-1;i=edge[i].next)
-
{
-
int v=edge[i].to;
-
if(edge[i].cap!=
0||dep[v]!=
-1)
continue;
-
que[rear++]=v;
-
if(rear==MAXN)rear=
0;
-
dep[v]=dep[u]+
1;
-
++gap[dep[v]];
-
}
-
}
-
}
-
int SAP(int start,int end)
-
{
-
int res=
0;
-
BFS(start,end);
-
int cur[MAXN];
-
int S[MAXN];
-
int top=
0;
-
memcpy(cur,head,
sizeof(head));
-
int u=start;
-
int i;
-
while(dep[start]<n)
-
{
-
if(u==end)
-
{
-
int temp=INF;
-
int inser;
-
for(i=
0;i<top;i++)
-
if(temp>edge[S[i]].cap)
-
{
-
temp=edge[S[i]].cap;
-
inser=i;
-
}
-
for(i=
0;i<top;i++)
-
{
-
edge[S[i]].cap-=temp;
-
edge[S[i]^
1].cap+=temp;
-
}
-
res+=temp;
-
top=inser;
-
u=edge[S[top]].from;
-
}
-
if(u!=end&&gap[dep[u]
-1]==
0)
//出现断层，无增广路
-
break;
-
for(i=cur[u];i!=
-1;i=edge[i].next)
-
if(edge[i].cap!=
0&&dep[u]==dep[edge[i].to]+
1)
-
break;
-
if(i!=
-1)
-
{
-
cur[u]=i;
-
S[top++]=i;
-
u=edge[i].to;
-
}
-
else
-
{
-
int min=n;
-
for(i=head[u];i!=
-1;i=edge[i].next)
-
{
-
if(edge[i].cap==
0)
continue;
-
if(min>dep[edge[i].to])
-
{
-
min=dep[edge[i].to];
-
cur[u]=i;
-
}
-
}
-
--gap[dep[u]];
-
dep[u]=min+
1;
-
++gap[dep[u]];
-
if(u!=start)u=edge[S[--top]].from;
-
}
-
}
-
return res;
-
}
给边赋值时，养成习惯用加法，防止有重边！
-
//****************************************************
-
//最大流模板
-
//初始化：g[][],start,end
-
//******************************************************
-
const
int MAXN=
110;
-
const
int INF=
0x3fffffff;
-
int g[MAXN][MAXN];
//存边的容量，没有边的初始化为0
-
int path[MAXN],flow[MAXN],start,end;
-
int n;
//点的个数，编号0-n.n包括了源点和汇点。
-
-
queue<
int>q;
-
int bfs()
-
{
-
int i,t;
-
while(!q.empty())q.pop();
//把清空队列
-
memset(path,
-1,
sizeof(path));
//每次搜索前都把路径初始化成-1
-
path[start]=
0;
-
flow[start]=INF;
//源点可以有无穷的流流进
-
q.push(start);
-
while(!q.empty())
-
{
-
t=q.front();
-
q.pop();
-
if(t==end)
break;
-
//枚举所有的点，如果点的编号起始点有变化可以改这里
-
for(i=
0;i<=n;i++)
-
{
-
if(i!=start&&path[i]==
-1&&g[t][i])
-
{
-
flow[i]=flow[t]<g[t][i]?flow[t]:g[t][i];
-
q.push(i);
-
path[i]=t;
-
}
-
}
-
}
-
if(path[end]==
-1)
return
-1;
//即找不到汇点上去了。找不到增广路径了
-
return flow[end];
-
}
-
int Edmonds_Karp()
-
{
-
int max_flow=
0;
-
int step,now,pre;
-
while((step=bfs())!=
-1)
-
{
-
max_flow+=step;
-
now=end;
-
while(now!=start)
-
{
-
pre=path[now];
-
g[pre][now]-=step;
-
g[now][pre]+=step;
-
now=pre;
-
}
-
}
-
return max_flow;
-
}
-
-
-
-
扫一扫
909
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
