AVL树

最新推荐文章于 2023-08-28 21:57:04 发布
最新推荐文章于 2023-08-28 21:57:04 发布
阅读量282 收藏
点赞数
CC 4.0 BY-SA版权
分类专栏： 数据结构 文章标签： avl 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/oracle_29/article/details/85719275

AVL树


AVL树就是平衡二叉树，平衡二叉树的每个节点左右子树的高度差不超过1.AVL树每个节点都有高度，节点的高度为左右子树的最高高度加1，节点在新增或删除时递归维护每个节点的高度，每次旋转也都需要维护节点的高度。AVL树是否需要旋转以及旋转方式都跟平衡因子相关，平衡因子为节点左子树的高度减去右子树的高度。

平衡二叉树的查询复杂度为O(Log2n)，当往平衡二叉树添加或删除节点时有可能会破坏平衡二叉树。需要通过旋转来恢复平衡。

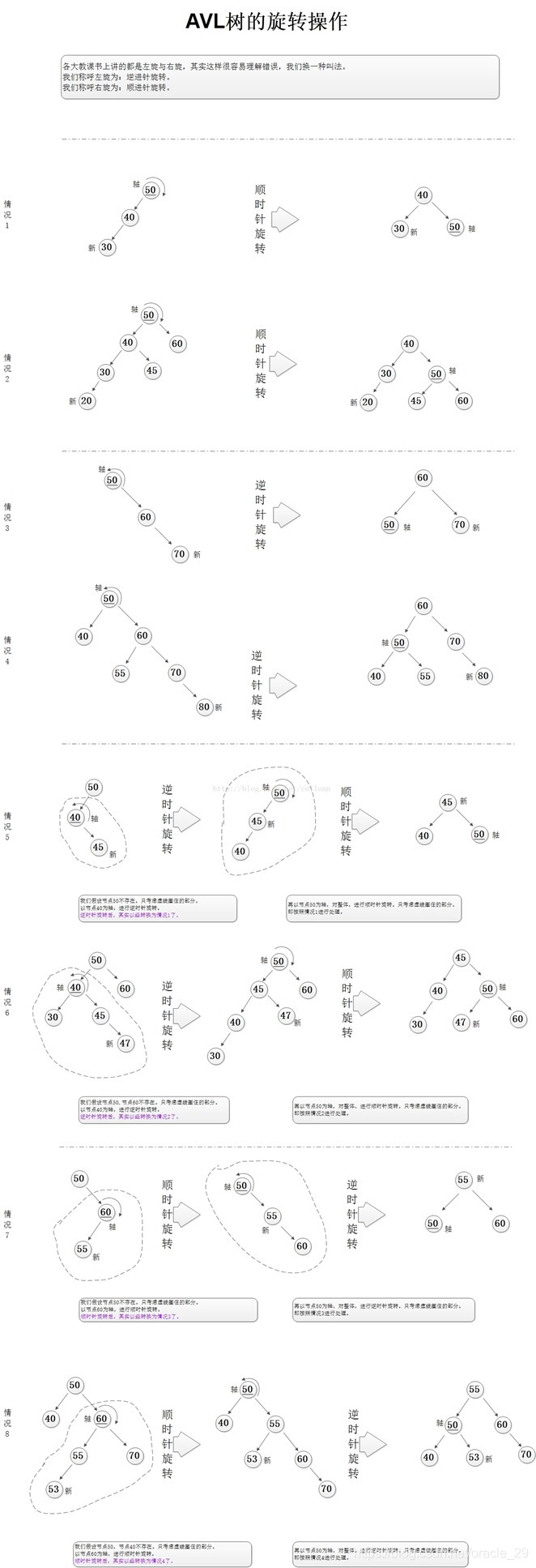
avl树每个节点平衡因子不为 1 ，0 ，-1话即为不平衡，左右子树高度差大于1。对于插入的节点，有以下4种情况会破坏平衡二叉树，每种情况需要不同的旋转方式

插入方式描述旋转方式
LL.在节点左子树的左侧插入节点（该节点的平衡因子为2且该节点左子树平衡因子为1）以该节点为轴右旋
RR在节点右子树的右侧插入节点（该节点的平衡因子为-2且该节点的右子树平衡因子为-1）以该节点为轴左旋
LR在节点左子树的右侧插入节点（该节点的平衡因子为2且该节点左子树的平衡因子为-1）以该节点左子树为轴先左旋，再以该节点为轴右旋
RL在节点的右子树左侧插入节点（该节点的平衡因子为-2且该节点右子树的平衡因子为1）以该节点右子树为轴先右旋，再以该节点为轴左旋

如果AVL树失衡旋转后需要网上递归检查到根节点的所有节点是否平衡，如果不平衡需要按上述规则旋转节点。

在这里插入图片描述
在这里插入图片描述

LeetCode 8.17 每日1题 110. 平衡二叉树
weixin_44601939的博客
08-18 481
LeetCode 8.17 每日1题 110. 平衡二叉树 给定一个二叉树，判断它是否是高度平衡的二叉树。 本题中，一棵高度平衡二叉树定义为： 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。 示例 1: 给定二叉树 [3,9,20,null,null,15,7] // An highlighted block var foo = 'bar'; ...
平衡二叉树
weixin_46033845的博客
09-02 463
左，右子树高度差的绝对值不超过1，定义结点左子树与右子树的高度差为该结点的平衡因子，则平衡二叉树结点的平衡因子的值只能是-1,0或1。
Leetcode—110： 平衡二叉树（两种解法）
yuiop123455的博客
10-31 814
题目描述： 给定一个二叉树，判断它是否是高度平衡的二叉树。 本题中，一棵高度平衡二叉树定义为： 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。 分析： 平衡二叉树的定义就是要求每个节点的左右两棵子树的高度差的绝对值不超过1，所以问题的关键就是需要求出每个节点的高度差，然后判断。 思路一： 考虑的关键：！！！ 一开始我思考能不能直接通过一个递归函数就把每一个节点的高度差计算出来，但是通过实践以及思考，发现：计算高度差必须先求出左右子树的高度，然后做差！如果直接将递归函数返回高度差，上一层的
B+树 中从根节点到每个叶子节点的高度差值不超过1是什么意思，画图解释一下...
weixin_35757191的博客
01-18 325
B树中从根节点到每个叶子节点的高度差值不超过1的意思是指B树的每一层的高度都相差不超过1。这是因为B树是一种平衡树，其目的是让每个节点的子节点数尽量平均，从而使得查询和插入的时间复杂度都能达到最优。 举个例子，若我们有一棵B树如下图所示，根节点为A，其左子节点为B，右子节点为C。B、C都是叶子节点，根节点A与B之间的高度差值为1，A与C之间的高度差值也为1。这就是B树中从根节点到每个叶子节点的高度...
计算机基础---＞数据结构（6）【AVL树（平衡二叉树）】
weixin_56781779的博客
07-04 715
平衡二叉树是一种特殊的二叉搜索树，他的左子树与右子树的高度差不超过1。保持平衡的特性使得平衡二叉树的查询、插入和删除操作在平均和最坏情况下的时间复杂度都是。右旋转和左旋转类似，右旋的方式是先将x节点的右子树单独定义出来为t2，然后将y节点连接到x的右子树，将t2连接到y的左子树上，这时就完成了右旋。首先创建节点用来保存树中的节点的数据，其次和二叉搜索树不同的是，AVL树需要平衡因子来控制二叉树的平衡。根据上图，我们可以直到，当二叉树的右树的高度超过平衡时需要进行左旋，，其中n是树中节点的数量。
AVL树数据结构平衡二叉查找树
07-16
在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者...
二叉查找树，AVL树
01-07
AVL树（平衡二叉查找树） 具有二叉查找树的全部特性。 每个节点的左子树的高度和右子树高度差值小于等于1（平衡二叉树的性质） 左旋：逆时针旋转两个节点，原先的右节点成为新的父节点，原先的父节点成为原先的右...
avlTree:通用AVL树数据结构
06-18
在AVL树中，任何节点的两个子子树的高度最多相差1； 如果在任何时候它们相差超过 1，则进行重新平衡以恢复此属性。 查找、插入和删除在平均和最坏情况下都需要 O(log n) 时间，其中 n 是操作之前树中的节点数。 ...
34平衡二叉树的定义
weixin_41883890的博客
01-17 613
平衡二叉树的定义：在插入和删除二叉树结点时，要保证任意结点的左右子树高度差的绝对值不超过1，将这样的二叉树称为平衡二叉树，简称AVL树 因此，平衡二叉树可定义为一颗空树或者具有下列性质的二叉树：它的左子树和右子树都是平衡二叉树，且左子树和右子树高度差的绝对值不超过1.如下所示，结点中的值为该结点的平衡因子 ...
了解平衡二叉树
zsx0728的博客
03-01 218
文章目录C示例平衡二叉树的应用参考文档     在本教程中，您将了解平衡的二叉树及其不同类型。此外，您还将在C中找到平衡二叉树的示例。     平衡二叉树，也称为高度平衡二叉树，是指任意节点左右子树的高度相差不超过1的二叉树。     以下是高度平衡二叉树的条件： 任何节点的左子树和右子树之间的差异不超过一个 左子树是平衡的 右子树是平衡的 C示例 // Checking if a binary tree is height balanced in C #include <stdio.h&g
平衡二叉树及其应用详解
sinat_30545761的博客
08-28 1132
平衡二叉树（Balanced Binary Tree）是计算机科学中的一种数据结构，它是二叉排序树的一种特殊情况。平衡二叉树满足以下性质：左子树和右子树的高度差不超过 1。也就是说，对于任意节点，其左子树和右子树的高度差不超过 1。左子树和右子树也都是平衡二叉树。平衡二叉树的定义可以通过递归的方式来定义。一棵高度为 h 的平衡二叉树，必须满足以下两个条件之一：该树为空，此时高度为 0。该树的左子树和右子树都是高度为 h-1 的平衡二叉树。
平衡二叉树（力扣）图解、思路与实现
weixin_45894950的博客
12-16 376
给定一个二叉树，判断它是否是高度平衡的二叉树。 本题中，一棵高度平衡二叉树定义为： 一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 /** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { thi
这可能是最简单的AVL二叉平衡查找树讲解
AD钙的博客
07-04 577
二叉平衡查找树AVL详解 看懂这篇文章所需的知识点 树、二叉搜索树、树高、树深、层等概念 AVL树 概念：任意节点的左右子树的高度差不能大于1的树即为AVL树，是为了解决在频繁插入删除等动态更新下出现的时间复杂度退化的问题，所以平衡的意思为：尽可能使整个树保持平衡，而不会出现左子树很高右子树很矮的情况。 AVL树失衡后平衡化操作分为四种：LL、RR、RL、LR LL的意思为：整棵树失衡的原因在于根节点的左节点的左节点导致的失衡，有可能是左节点的左节点本身（即一条链的情况）导致的失衡，或者是左节点的左节点上多
Avl树
最新发布
07-07
AVL树是一种自平衡的二叉查找树，它确保了树的高度始终保持在对数级别，从而保证了查找、插入和删除操作的时间复杂度为O(log n)。这种数据结构以它的发明者G.M. Adelson-Velsky和E.M. Landis的名字命名[^1]。 ### AVL树的定义 - **平衡因子**：每个节点都有一个平衡因子，它是该节点左子树的高度减去右子树的高度。对于AVL树来说，所有节点的平衡因子只能是-1, 0或1。 - **空树**：如果T是空树，则它自然是一个AVL树。 - **非空树**：若T不是空树，则其左右子树TL和TR都必须是AVL树，并且对于任意节点，|HL - HR| ≤ 1（其中HL和HR分别表示左子树和右子树的高度）。 ### AVL树的操作 当进行插入或删除操作时，可能会破坏AVL树的平衡性，这时需要通过旋转来重新恢复平衡： - **单旋转**： - 左单旋（Single Rotate with Left）用于处理左孩子的左子树过高。 - 右单旋（Single Rotate with Right）用于处理右孩子的右子树过高。 - **双旋转**： - 左右双旋（Double Rotate with Left）用于处理左孩子的右子树过高的情况。 - 右左双旋（Double Rotate with Right）用于处理右孩子的左子树过高的情况。 这些旋转操作可以保持AVL树的性质不变，并且能够快速地调整树的结构以维持平衡。 ### AVL树的实现 下面是一个简单的C语言代码示例，展示了如何定义AVL树的节点以及实现基本的插入操作。这个例子中包含了必要的函数声明和一些核心逻辑。 ```c #include <stdio.h> #include <stdlib.h> // 定义AVL树节点结构体 typedef struct AvlNode { int element; struct AvlNode *left; struct AvlNode *right; int height; // 节点的高度 } *AvlTree, *Position; // 获取两个整数中的较大者 int max(int a, int b) { return (a > b) ? a : b; } // 计算给定节点的高度 static int Height(AvlTree T) { if (T == NULL) return -1; // 空节点高度为-1 else return T->height; } // 单旋转 - 左左情况 AvlTree singlerotatewithLeft(AvlTree K2) { Position K1 = K2->left; K2->left = K1->right; K1->right = K2; // 更新节点高度 K2->height = max(Height(K2->left), Height(K2->right)) + 1; K1->height = max(Height(K1->left), K2->height) + 1; return K1; // 新根 } // 单旋转 - 右右情况 AvlTree singlerotatewithRight(AvlTree K2) { Position K1 = K2->right; K2->right = K1->left; K1->left = K2; // 更新节点高度 K2->height = max(Height(K2->left), Height(K2->right)) + 1; K1->height = max(Height(K1->right), K2->height) + 1; return K1; // 新根 } // 双旋转 - 左右情况 AvlTree doublerotatewithLeft(AvlTree K3) { K3->left = singlerotatewithRight(K3->left); return singlerotatewithLeft(K3); } // 双旋转 - 右左情况 AvlTree doublerotatewithRight(AvlTree K3) { K3->right = singlerotatewithLeft(K3->right); return singlerotatewithRight(K3); } // 插入新元素到AVL树中 AvlTree Insert(int x, AvlTree T) { if (T == NULL) { // 如果树为空，创建新节点 T = (AvlTree)malloc(sizeof(struct AvlNode)); if (T == NULL) printf("Out of space!!!"); else { T->element = x; T->left = T->right = NULL; T->height = 0; // 新叶节点高度为0 } } else if (x < T->element) { // 向左子树插入 T->left = Insert(x, T->left); // 检查并修复平衡 if (Height(T->left) - Height(T->right) == 2) { if (x < T->left->element) T = singlerotatewithLeft(T); // 左左旋转 else T = doublerotatewithLeft(T); // 左右旋转 } } else if (x > T->element) { // 向右子树插入 T->right = Insert(x, T->right); // 检查并修复平衡 if (Height(T->right) - Height(T->left) == 2) { if (x > T->right->element) T = singlerotatewithRight(T); // 右右旋转 else T = doublerotatewithRight(T); // 右左旋转 } } // 更新高度 T->height = max(Height(T->left), Height(T->right)) + 1; return T; } ``` 上述代码提供了AVL树的基本框架，包括节点定义、插入操作及必要的旋转方法。实际应用中可能还需要添加更多的功能，如删除节点、查找特定值等。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值