算法：102 二叉树的层序遍历和每层最大值

102. 二叉树的层序遍历

层序遍历 

给你二叉树的根节点 root ，返回其节点值的 层序遍历 。 （即逐层地，从左到右访问所有节点）。

示例 1：

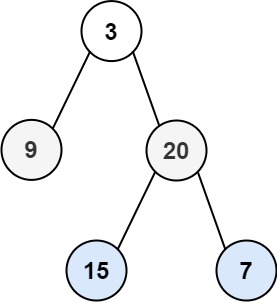
输入：root = [3,9,20,null,null,15,7]
输出：[[3],[9,20],[15,7]]

示例 2：

输入：root = [1]
输出：[[1]]

示例 3：

输入：root = []
输出：[]

提示：

• 树中节点数目在范围 [0, 2000] 内
• -1000 <= Node.val <= 1000

在Java中，二叉树的分层遍历通常指的是层序遍历（Breadth-First Search, BFS），它按照树的层次顺序访问节点。为了实现这个功能，我们可以使用队列（Queue）来辅助遍历。下面是一个简单的Java代码示例，用于实现二叉树的分层遍历，并附带了详细的说明。
首先，我们需要定义二叉树节点的数据结构：

public class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;

    TreeNode(int x) {
        val = x;
    }
}

接下来是实现分层遍历的Java方法：
 

import java.util.LinkedList;
import java.util.Queue;

public class BinaryTreeLevelOrderTraversal {

    // 二叉树的分层遍历（层序遍历）
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root == null) {
            return result;
        }

        // 使用队列来进行层序遍历
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root); // 将根节点加入队列

        while (!queue.isEmpty()) {
            // TreeNode node = queue.poll(); 错误提示

            int levelSize = queue.size(); // 当前层的节点数量
            List<Integer> levelNodes = new ArrayList<>(); // 存储当前层的节点值

            // 遍历当前层的所有节点
            for (int i = 0; i < levelSize; i++) {
                TreeNode currentNode = queue.poll(); // 取出队首节点
                levelNodes.add(currentNode.val); // 将节点值加入当前层列表

                // 将当前节点的子节点加入队列
                if (currentNode.left != null) {
                    queue.offer(currentNode.left);
                }
                if (currentNode.right != null) {
                    queue.offer(currentNode.right);
                }
            }

            // 当前层遍历完毕，将当前层的节点值列表加入结果列表
            result.add(levelNodes);
        }

        return result;
    }

    // 主函数用于测试
    public static void main(String[] args) {
        // 构造一个简单的二叉树进行测试
        TreeNode root = new TreeNode(3);
        root.left = new TreeNode(9);
        root.right = new TreeNode(20);
        root.right.left = new TreeNode(15);
        root.right.right = new TreeNode(7);

        BinaryTreeLevelOrderTraversal traversal = new BinaryTreeLevelOrderTraversal();
        List<List<Integer>> result = traversal.levelOrder(root);

        // 输出分层遍历的结果
        for (List<Integer> level : result) {
            System.out.println(level);
        }
    }
}

详细说明：
定义数据结构：首先，我们定义了一个TreeNode类来表示二叉树的节点，包含节点的值以及左右子节点的引用。
实现分层遍历：在BinaryTreeLevelOrderTraversal类中，我们实现了levelOrder方法来进行分层遍历。该方法接收一个TreeNode类型的根节点作为参数，并返回一个二维列表List<List<Integer>>，其中每个内部列表List<Integer>代表一层节点的值。
使用队列：我们使用了Java的LinkedList作为队列来实现层序遍历。队列的特性是先进先出（FIFO），非常适合用来进行层次遍历。
遍历过程：
首先，检查根节点是否为空，如果为空则直接返回空结果列表。
将根节点加入队列。
当队列不为空时，进行循环遍历。在每次循环中，首先获取当前层的节点数量levelSize，然后遍历当前层的所有节点。对于每个节点，将其值加入当前层的列表levelNodes，并将其子节点（如果存在）加入队列。
当当前层的所有节点都遍历完毕后，将当前层的节点值列表levelNodes加入结果列表result。
主函数测试：在main方法中，我们构造了一个简单的二叉树，并调用levelOrder方法进行测试。最后，我们遍历结果列表并打印每一层的节点值。
通过上面的代码和说明，你应该能够清楚地理解如何在Java中实现二叉树的分层遍历。

每层最大值 

	public List<Integer> findMaxvalue(TreeNode root) {
		List<Integer> maxValuseIntegers = new ArrayList<Integer>();
		if (root == null) {
			return maxValuseIntegers;
		}
		
		Queue<TreeNode> queue = new LinkedList<TreeNode>();
		queue.offer(root);
		
		while(!queue.isEmpty()) {
			int levelMaxValue = Integer.MIN_VALUE;
			// 这个地方是关键
			int levelSize = queue.size();
			for (int i = 0; i < levelSize; i++) {
				TreeNode node = queue.poll();
				levelMaxValue = Math.max(levelMaxValue, node.val);
				
				if (node.left != null) {
					queue.offer(node.left);
				}
				
				if (node.right != null) {
					queue.offer(node.right);
				}
			}
			maxValuseIntegers.add(levelMaxValue);
		}
		return maxValuseIntegers;
	}