对称密码分析技术：经典方法、现代演进与攻防博弈

原创已于 2025-10-20 14:25:18 修改 · 706 阅读

9 ·

CC 4.0 BY-SA版权

文章标签：

#对称密码算法 #AES #后量子密码 #截断差分 #不可能差分 #差分密码分析 #线性密码分析

于 2025-10-20 14:18:22 首次发布

密码学实战同时被 2 个专栏收录

65 篇文章

订阅专栏

密码学基础

59 篇文章

订阅专栏

前言

在数字世界的安全战场上，密码算法是守护信息的“盾牌”，而密码分析则是攻击者手中的“长矛”——这场攻防对抗从密码诞生之日起就从未停歇。我们每天使用的微信聊天端到端加密、支付宝/微信支付的资金流传输、手机锁屏的PIN码验证，背后依赖AES、SM4等对称密码算法；企业内部的财务报表流转、云端存储的用户身份证照片、甚至国家外交的敏感通信数据，同样需要对称密码构建第一道安全防线。这些算法就像数字世界的“锁芯”，而密码分析则是“锁匠与小偷的博弈”——既要破解脆弱的锁芯，也要检验坚固锁芯的可靠性。

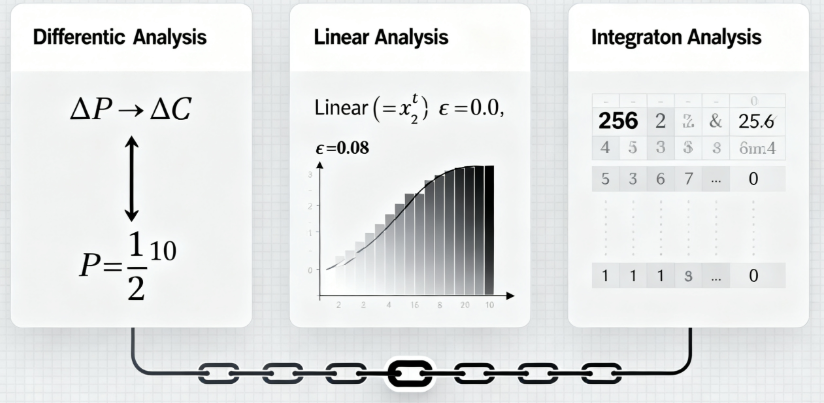
对称密码分析正是“攻防两端的试金石”：攻击者借助它突破防线，小到通过破解弱密码盗刷银行卡，大到国家级黑客组织利用漏洞窃取商业机密；密码设计者则依靠它检验算法的坚固程度，在算法公开前主动发起“内部攻击”，修补潜在漏洞。这种“以攻促防”的持续博弈，推动密码学完成了从古代凯撒密码（字母移位替换）、中世纪维吉尼亚密码（多表替换），到近代DES（数据加密标准），再到如今能抵御量子攻击的AES-256、SM4等高级算法体系的跨越式进化。

1. 基础篇：经典密码分析的“三板斧”

这三种经典方法是密码分析的“入门基石”，诞生于20世纪80-90年代，分别从“差分传播”“线性关联”“集合性质”三个维度挖掘密码算法的数学漏洞。它们不仅奠定了现代对称密码分析的理论框架，至今仍是研究轻量级密码、简化轮高级密码的重要工具，许多现代攻击方法（如截断差分、积分-线性混合攻击）都源于这些经典思想的延伸。

1.1 差分密码分析：追踪“变化的痕迹”

核心思想：就像侦探观察两个相似案件（如同一地点的两起盗窃案）的差异（作案工具、时间间隔）来锁定嫌疑人，差分分析关注“明文微小变化如何在加密过程中被放大或传递”。假设给明文P加一个“变化标记”ΔP（即P和P'进行异或运算，异或是密码学中表示“变化”的常用操作），追踪这个标记经过多轮加密变换后，最终变成的输出差异ΔC（C和C'异或）。如果某组（ΔP, ΔC）出现的概率远高于随机水平（比如超过10%），就说明加密过程中存在“概率偏倚”，对应的密钥比特可能藏着可利用的“漏洞”。

技术拆解：

特征查找：攻击者先“绘制”高概率变化路径，核心是分析算法的非线性组件S盒（替换盒，将n位输入映射为n位输出，非线性是抵抗线性攻击的关键）。比如某4位S盒，输入差分为0x01（二进制0001）时，输出差分为0x03的次数为1次，总输入组合16种，概率即1/16。之后串联多轮S盒和线性变换（移位、异或）的差分概率，用“概率乘法原理”计算多轮总概率，最终找到贯穿多轮、总概率高于1/2¹⁰的“大概率通道”。这一步常需编程遍历上万条路径，是差分分析最耗时的环节。
密钥恢复：找到“通道”后，攻击者需收集大量符合输入差分ΔP的明密文对，数量由路径概率决定——概率1/2¹⁶的路径需2¹⁸对左右（保证统计显著性）。在加密“最后一站”（通常是最后一轮），用输出差分ΔC反推轮密钥：假设某4位轮密钥为0101，将密文与假设密钥做轮解密，检查中间值是否符合差分通道预期。统计所有明密文对的符合次数，次数最高的密钥组合就是最可能候选，逐步扩展到完整轮密钥，最终恢复初始密钥。

应用场景：差分密码分析由Biham和Shamir于1990年提出，首次公开攻破了16轮DES的简化版本（8轮），震惊密码学界。早期主要用于攻击DES、FEAL（一种早期分组密码，因结构简单被差分分析快速攻破）等算法；如今仍是分析轻量级密码（如PRESENT、LED，用于物联网设备）的重要工具。例如2021年密码学者对6轮PRESENT的差分攻击，仅需2¹⁶个明密文对，在普通计算机上耗时不到1小时即可恢复64位密钥。

1.2 线性密码分析：寻找“秘密等式”

核心思想：差分分析盯“变化的传播”，线性分析则找“比特间的关联”——挖掘输入比特子集、输出比特子集与密钥比特子集之间的“线性等式”。线性等式的形式为“P[i₁]⊕P[i₂]⊕…⊕C[j₁]⊕C[j₂]⊕…=K[k₁]⊕K[k₂]⊕…”，其中⊕表示异或运算。在理想的随机密码中，该等式成立的概率应为50%（像抛硬币正反面概率相等）；若实际概率偏离50%（即偏差ε=|p-1/2|≠0），就说明三者之间存在非随机关联，这就是攻击的突破口。偏差ε越大，关联越强，攻击所需的明密文对数量越少，攻击效率越高。

技术拆解：

堆积引理：线性分析的“组合神器”，由Matsui于1993年提出。核心是：两个独立线性逼近的偏差ε₁和ε₂，组合后新偏差ε≈2ε₁ε₂（ε较小时）。实际多轮组合需逐步叠加，比如10个偏差0.01-0.03的弱逼近，可组合成偏差0.08-0.1的强逼近。这就像10块各吸1张纸的弱磁铁，合理排列后拼成吸8张纸的强磁石，是构建多轮线性攻击路径的核心支撑。
数据复杂度：攻击所需明密文对数量与偏差平方成反比，理论公式N≈1/(2ε²)。但实际需考虑统计置信度，通常要乘以10-100的系数。比如Matsui 1994年攻击完整16轮DES时，最佳线性逼近偏差约0.004，需约2⁴³个已知明文（约8.7万亿亿个）。这个数量远超当时计算存储能力，但理论上首次打破“完整16轮DES不可破解”的认知，推动DES淘汰和AES选拔。

应用场景：线性密码分析广泛用于攻击AES简化轮、Camellia（日本商业密码标准）、IDEA（早期国际分组密码）等算法。2019年，德国达姆施塔特工业大学的研究者利用改进的线性分析方法，成功攻击了8轮AES-128，所需已知明文数量约为2⁴⁵个，在超级计算机上需数天时间完成统计分析；2023年，针对轻量级密码Midori的线性攻击仅需2³⁰个明文，在普通服务器上即可实现。

1.3 积分密码分析：玩转“特殊明文军团”

核心思想：不同于差分和线性分析使用随机或特定差分/线性的明文，积分密码分析派一支“结构特殊的明文军团”——选择一组明文，其中某个字节（称为“活跃字节”）遍历0-255所有可能值，其余字节（称为“固定字节”）保持不变，形成包含256个明文的“积分集合”。这些明文经过多轮加密后，观察其对应密文在某个特定函数（如异或和、零和、汉明重量和）下的“集体行为”，例如所有密文的第3个字节异或和恒为0。这种规律性是密码算法结构带来的“固有漏洞”，而随机明文集合几乎不可能呈现如此严格的集体性质。

技术拆解：

区分器构建：攻击核心是找到“积分区分器”——确定经过多少轮加密后，积分集合的密文会呈现特定集体性质。比如AES的3轮积分区分器：选“第1字节活跃，其余固定”的256个明文，经3轮加密后，所有密文任意字节的异或和必为0。这种“无论初始固定字节是什么，加密后异或和恒为0”的铁律，是积分攻击的关键突破口。区分器轮数越长，能攻击的密码轮数也越多。
密钥恢复：用积分区分器恢复密钥时，采用“从后往前推”策略：先猜测最后一轮轮密钥的部分比特（通常8位或16位，对应1-2个S盒输入），用猜测密钥对密文做“部分解密”（仅执行最后一轮逆变换，如AES的逆字节代换、逆行移位），得到“中间状态”。验证中间状态是否满足区分器性质（如异或和为0），满足则保留密钥猜测，否则排除。逐步扩展猜测比特长度，像“筛子”滤掉错误密钥，最终确定完整轮密钥并反推初始密钥。

应用场景：积分密码分析由Daemen等人于1997年在攻击Square密码时提出，因此也称为“Square攻击”。它专门针对具有“字节代换-线性变换”（Substitution-Permutation Network，SPN）结构的算法，如AES、Square、Midori、GIFT等。对于AES简化轮，积分攻击是效率最高的方法之一——攻击4轮AES-128仅需2⁸个明密文对，5轮需2¹⁶对，6轮需2²⁴对，在普通计算机上几分钟内即可完成密钥恢复。

1.4 经典方法对比：一张表看懂核心差异

分析方法	核心逻辑	关键指标	数据复杂度量级	典型攻击对象
差分密码分析	追踪差分传播概率	差分路径概率	2¹⁶-2³²	DES、FEAL、PRESENT
线性密码分析	寻找线性逼近关系	偏差ε	2⁴⁰-2⁵⁰	DES、AES简化轮、Camellia
积分密码分析	利用明文集合集体性质	积分区分器轮数	2⁸-2¹⁶	AES、Square、Midori

2. 进阶篇：现代攻击的“升级玩法”

随着AES等高级密码算法采用更复杂的SPN结构、更优的S盒设计和多轮加密，传统的差分、线性分析难以突破完整轮算法。为此，攻击者转向“灵活化、场景化”的进阶分析思路——或放宽差分的精确性约束，或利用密钥间的关联性，或结合多种方法的优势，大幅拓展了攻击的适用范围和效果。

2.1 截断差分与不可能差分：换个角度“找漏洞”

截断差分：由Knudsen于1995年提出，核心是不纠结差分值的完整比特，只关注部分比特状态特征，主要分三类：

- 字节截断：关注某字节是否为非零（记为Δ）；

- 比特截断：关注某4位是否为非零；

- 掩码截断：关注高8位是否为0x00。

这种“抓大放小”策略大幅扩大搜索空间——比如传统差分需精确匹配32位差分，字节截断后只需匹配4个字节是否非零，搜索范围从2³²缩小到2⁴，效率提升百万倍。就像侦探追查嫌疑人，不用看清完整面容，记“身高180cm左右、穿蓝色外套”就能快速排查。

应用案例：2018年中科院团队用字节截断差分，将AES-192攻击轮数从5轮提至7轮（需2⁴⁸个明密文对）；2022年针对轻量级密码Grain-128a的截断差分攻击，成功恢复128位密钥。

不可能差分：由Biham等人于1997年提出，利用“概率为0的差分路径”——无论密钥如何，某输入差分经特定轮数加密后，绝不可能得到某输出/中间状态差分（如输入差分为0x01时，2轮后中间状态绝不可能是0x02）。攻击者核心操作是“排除法”：收集大量明密文对，假设某密钥候选成立，推导中间状态差分是否落入“不可能”范围，若是则排除该密钥。这种“证伪式”攻击能大幅减少密钥候选量，比如从2¹²⁸个中排除99%，仅剩2¹²⁶个，显著提升效率。 应用案例：2011年用不可能差分攻击攻破9轮AES-256（当时攻击轮数最多）；2020年针对SM4的不可能差分攻击，攻破8轮（需2⁵⁶个明密文对）。

2.2 相关密钥攻击：盯上“关联的钥匙”

攻击逻辑：由Biham于1993年提出，攻击模型假设攻击者能获取“相关密钥”加密的明密文对——相关密钥通常通过简单运算关联，如K₁=K⊕Δ、K₂=K⊕Γ（Δ、Γ为固定非零常数）。攻击关键是利用密钥扩展算法缺陷：若扩展过程存在线性或低非线性变换，相关密钥生成的轮密钥会呈现可预测关联（如轮密钥差分为固定值）。攻击者分析这种关联在密文中的体现，建立方程反推初始密钥。 防御要点：实际防御核心是确保密钥独立性——密码设备需用符合NIST标准的真随机数生成器（如TRNG）每次生成全新独立密钥，避免密钥关联。AES-128因密钥扩展设计严谨，至今未被相关密钥攻击攻破；AES-192/256因扩展步骤少，部分版本曾被混合攻击攻破简化轮。

2.3 现代攻击效果对比

关键结论：

三种进阶方法各有优势——截断差分通过放宽差分约束，适合拓展攻击轮数（比传统差分多2-3轮）；不可能差分通过“证伪”策略，适合降低密钥候选量（减少1-2个数量级）；相关密钥攻击需特定场景（密钥可关联），但能突破普通攻击无法攻破的轮数。

三者结合可形成更强大的混合攻击，例如“相关密钥-截断差分攻击”“相关密钥-不可能差分攻击”等。2019年，研究者利用“相关密钥-不可能差分攻击”成功攻破了11轮Camellia-256算法，是该算法目前的最佳攻击结果；2023年，针对轻量级密码ACORN的“差分-相关密钥混合攻击”，将攻击数据复杂度降低了3个数量级。

3. 防御篇：密码设计者的“筑墙之道”

面对差分、线性、相关密钥等多样的攻击手段，现代密码设计者不再依赖单一防御措施，而是构建了“算法结构+参数选择+实现优化”的多层次防御体系。从算法设计初期就融入抗攻击思想，通过严格的安全性分析和公开评审，确保算法能抵御已知的主流攻击，同时为未来可能出现的新型攻击预留安全冗余。

3.1 核心防御策略

宽轨迹策略：AES核心防御策略，由Daemen和Rijmen提出。通过字节代换（SubBytes）、行移位（ShiftRows）、列混合（MixColumns）协同作用，确保任意两轮间“活跃S盒”（输入差分非零的S盒）至少4个。活跃S盒越多，差分路径概率越低：1个最大概率约1/4，2个为(1/4)²=1/16，4个则为(1/4)⁴=1/256，多轮累积后概率低于1/2¹²⁸（低于暴力破解复杂度）。这就像在城堡间修满交错荆棘丛和护城河，让攻击者找不到可利用的高概率通道。
安全冗余设计：通过设置远超“当前攻击轮数”的加密轮数，为算法提供长期安全性。例如AES-128设计了10轮加密，目前密码学界能攻击的最大轮数为7轮（不可能差分攻击），多的3轮是“安全缓冲垫”；AES-256设计32轮，当前最大攻击轮数为9轮，冗余轮数达23轮。除了轮数冗余，还有密钥长度冗余——如DES的56位密钥已被暴力破解，而AES-128的128位密钥在量子计算前仍安全。3DES算法则通过“加密-解密-加密”的三次DES操作实现冗余，即使单轮DES的56位密钥不安全，三次组合后等效密钥长度达112位，能抵御暴力攻击。
非线性优化：S盒的非线性是抵抗线性攻击的关键，设计者通过严格筛选S盒，确保其具有高非线性度、低差分均匀度和良好的代数免疫性。例如SM4的S盒采用8位输入输出，其非线性度达112（最高为120，越接近越好），最大差分均匀度为4（最低为2，越小越好），远优于普通S盒的性能；AES的S盒非线性度为110，最大差分均匀度为4，能有效压低线性逼近偏差和差分概率，让传统攻击难以奏效。

3.2 典型防御案例：AES的“铜墙铁壁”

AES作为全球应用最广的对称密码标准（用于云计算、移动支付、操作系统加密等），防御体系是现代密码设计的标杆：

1. 宽轨迹策略为核心：SubBytes、ShiftRows、MixColumns交替执行，确保活跃S盒数量充足，抵御差分/线性攻击；

2. 充足安全冗余：AES-128/192/256分别设10/12/14轮加密，远超当前最大攻击轮数（AES-128最多7轮），应对未来技术进步；

3. 平衡变换组合：字节代换提供非线性，行移位和列混合提供扩散性（让明文变化快速传播到整个密文），打破攻击路径规律性；

4. 严谨密钥扩展：AES-128通过循环移位、S盒替换和轮常量异或，确保轮密钥独立性，抗相关密钥攻击。

至今，完整轮AES-128/192/256未被任何实用攻击攻破，是NIST推荐的长期安全算法。

4. 未来展望：攻防博弈的“新战场”

随着量子计算、人工智能技术的快速发展，以及物联网、全同态加密等新应用场景的涌现，对称密码的攻防博弈正进入更复杂、更精细的新阶段。攻击端借助AI提升分析效率，防御端则针对新威胁优化算法设计，双方的技术竞争推动着密码学不断向前发展。

4.1 技术趋势细分

攻击端创新

AI辅助分析：用深度学习模型（CNN、LSTM）预测S盒差分/线性概率，效率比手工计算提升数百倍；用强化学习自动搜索最优差分路径，2022年某团队用RL找到的AES差分路径概率比人工结果高3个数量级；
自动化工具：基于约束求解器（如Z3、CVC4）和符号执行工具（如Klee）自动生成积分区分器、线性逼近关系，2023年开源工具AutoCrypt已能自动分析轻量级密码的6轮积分区分器；
混合攻击：结合多种方法，如“差分-积分混合攻击”突破更多轮数。

防御端升级

后量子密码：推广AES-256、SM4-256等长密钥算法，Grover算法会将密钥搜索复杂度从O(2ⁿ)降至O(2ⁿ/²)，256位密钥可抵御量子攻击；同时研究新型后量子对称密码，如NIST正在评审的轻量级后量子标准；
轻量级优化：在物联网设备中平衡效率与安全性；
形式化验证：用数学证明确保算法无设计漏洞。