中间相遇攻击：密码学中的分治颠覆者

引言：多重加密的困境与破局

在密码学的发展历程中，一个直观的增强安全性的想法是进行多次加密。如果一次加密是安全的，那么两次、三次理应更加安全——这一朴素认知曾广泛存在于早期密码设计中。然而，1977年中间相遇攻击（Meet-in-the-Middle Attack）的提出，彻底颠覆了这一观念，它以"分而治之"的巧妙思路，揭示了叠加安全性背后的复杂本质，成为密码分析史上的经典范式。

1.1 安全增强的朴素思路

面对一个密钥长度为 n 位的分组密码（如DES，n=56），其理论安全强度由密钥空间大小决定，即 2^n 种可能的密钥组合。上世纪70年代，随着计算能力的提升，56位DES的密钥空间逐渐显露出被暴力破解的风险。为应对这一威胁，最直接的方案是采用"双重加密"：连续使用两个独立密钥 K1 和 K2 对明文进行两次加密，即 C = E(K2, E(K1, P))（其中E表示加密函数，P为明文，C为密文）。从直觉上看，密钥空间从 2^n 扩大到 2^n * 2^n = 2^(2n)，暴力破解的尝试次数应呈指数级增长，安全性似乎得到了平方级提升。

1.2 暴力破解的维度灾难

对于双重加密方案，传统暴力破解需遍历所有可能的 (K1, K2) 密钥对。以双重DES为例，密钥空间达到 2^112——这是一个极其庞大的数字：若一台计算机每秒能完成10亿次加密操作，遍历整个密钥空间需要约 10^25 年，远超当前宇宙约138亿年的年龄。这种“维度灾难”（简单说就是变量太多导致计算量爆炸）似乎为双重加密筑起了坚不可摧的安全壁垒，使其在理论上具备了极强的抗攻击性。

1.3 中间相遇攻击的诞生与哲学

中间相遇攻击由密码学先驱W. Diffie和M. Hellman在1977年发表的《密码学的新方向》后续研究中提出，它如同一把精巧的钥匙，巧妙绕过了暴力破解的计算壁垒。其核心哲学在于“分而治之”与“空间换时间”的协同：攻击者不再同时处理两个密钥，而是将两次加密的过程从中间“切断”，分别从明文端和密文端向中间的“过渡值”推进，最终在中间点完成匹配。这种策略将原本“乘性”的复杂度（2^(2n)）戏剧性地降低为“加性”级别（2^(n+1)），彻底改变了多重加密的安全格局。

2. 攻击核心原理剖析

2.1 分治思想在密码分析中的应用

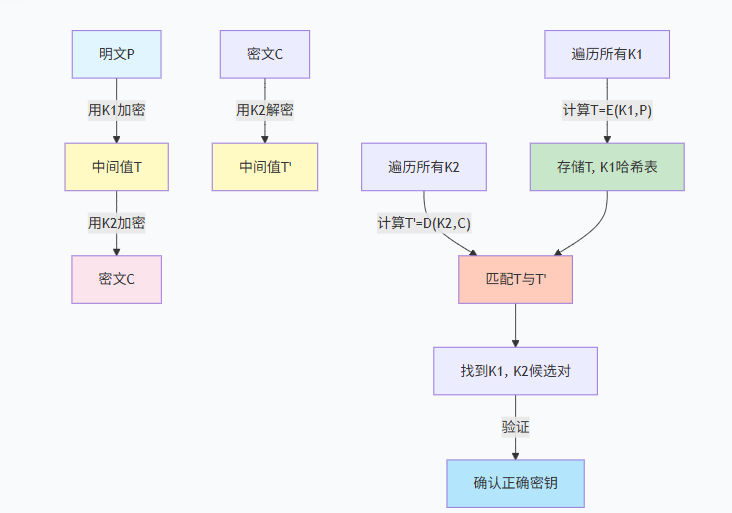
中间相遇攻击是分治策略（Divide and Conquer）在密码分析领域的完美实践。分治策略的核心是将复杂问题拆解为若干可独立解决的子问题，通过解决子问题来聚合出原问题的解。在双重加密场景中，“破解 (K1, K2) 密钥对”这一单一复杂问题被拆解为两个独立的子问题：

1. 问题A（明文端正向计算）：给定已知明文 P，遍历所有可能的 K1，计算中间过渡值 T = E(K1, P)；

2. 问题B（密文端逆向计算）：给定对应密文 C，遍历所有可能的 K2，计算中间过渡值 T' = D(K2, C)（其中D表示解密函数）。

3. 问题A（明文端正向计算）：给定已知明文 P，遍历所有可能的 K1，计算中间过渡值 T = E(K1, P)；

4. 问题B（密文端逆向计算）：给定对应密文 C，遍历所有可能的 K2，计算中间过渡值 T' = D(K2, C)（其中D表示解密函数）。

咱们用“找两把钥匙开双层门”来类比：假设你要进一个有两重门的房间，每道门都有自己的钥匙（K1对应第一道，K2对应第二道）。暴力破解就是把所有钥匙两两配对试（比如1号+1号、1号+2号……），要试完所有组合才知道哪对能开门。而中间相遇攻击就像：你先站在门外，用所有可能的K1试开第一道门，每打开一道就在门后放一张写着“K1编号”的纸条；然后你绕到房间里，用所有可能的K2试开第二道门，每打开一道就看门口有没有纸条——如果有，那纸条上的K1和你手里的K2就是配对的钥匙！

由于双重加密的本质是 C = E(K2, T)，等价于 T = D(K2, C)，因此原问题的解就是找到使得 T = T' 的 (K1, K2) 对。这种拆解将“同时破解两个密钥”的高难度任务，转化为“分别计算中间值并匹配”的低复杂度任务。

2.2 攻击的通用模型

前提假设：攻击者需掌握至少一对“已知明文-密文对”（Plaintext-Ciphertext Pair, P-C Pair），即 (P1, C1)；为消除碰撞导致的伪阳性结果，通常还需额外一对验证用的 (P2, C2)。这一假设在现实中具有合理性——例如攻击者可能通过观察加密系统的输入输出获取此类数据。

算法描述：

1. 建表阶段（正向计算）：遍历所有可能的 K1（共 2^n 个），对已知明文 P1 执行加密操作，得到中间值 T_i = E(K1_i, P1)。将所有 (T_i, K1_i) 对存储在查找表中，并按 T_i 进行排序或构建哈希表（哈希表可将查询时间降至O(1)，是实际攻击中的首选）。

2. 搜索阶段（逆向计算）：遍历所有可能的 K2（共 2^n 个），对已知密文 C1 执行解密操作，得到中间值 T'_j = D(K2_j, C1)。

3. 匹配阶段：对每个计算出的 T'_j，在查找表中查询是否存在相同的 T_i。若存在，则对应的 (K1_i, K2_j) 构成候选密钥对。

4. 验证阶段：由于分组密码存在“碰撞”可能（不同密钥对可能产生相同中间值），需使用验证对 (P2, C2) 测试候选密钥对——若 E(K2, E(K1, P2)) == C2，则该密钥对为正确解。

代码示例：

def meet_in_the_middle(P1, C1, P2, C2, encrypt, decrypt, key_space):
    # 1. 建表阶段：存储K1与对应的中间值T
    lookup_table = {}
    for K1 in key_space:
        T = encrypt(K1, P1)
        lookup_table[T] = K1  # 以中间值为键，K1为值
    
    # 2. 搜索与匹配阶段
    candidate_keys = []
    for K2 in key_space:
        T_prime = decrypt(K2, C1)
        if T_prime in lookup_table:
            K1_candidate = lookup_table[T_prime]
            candidate_keys.append( (K1_candidate, K2) )
    
    # 3. 验证阶段：筛选正确密钥对
    correct_keys = []
    for K1, K2 in candidate_keys:
        if encrypt(K2, encrypt(K1, P2)) == C2:
            correct_keys.append( (K1, K2) )
    
    return correct_keys

2.3 复杂度分析：时间与空间的权衡

中间相遇攻击的核心优势在于通过牺牲存储空间降低计算时间，其复杂度分析如下：

• 时间复杂度：建表阶段需执行 2^n 次加密，搜索阶段需执行 2^n 次解密，总时间复杂度为 O(2^n) + O(2^n) = O(2^(n+1))。以DES为例（n=56），总计算量约为 2^57 次操作，远低于暴力破解的 2^112。

• 空间复杂度：需存储 2^n 个 (T_i, K1_i) 对。若每个条目占16字节（8字节T值+8字节K1），对于n=56，存储量约为 2^56 * 16字节 ≈ 2.3PB（1PB=1024TB）。

与暴力破解的对比：

攻击方式	时间复杂度	空间复杂度	核心瓶颈
暴力破解（双重加密）	O(2^(2n))	O(1)	计算时间过长
中间相遇攻击	O(2^n)	O(2^n)	存储资源占用过大

3. 经典案例：双重DES的陷落

DES（Data Encryption Standard）作为上世纪70-90年代的主流分组密码，其56位密钥在1999年被EFF（电子前哨基金会）的“DES破解机”以22小时破解，证明了短密钥的脆弱性。双重DES曾被视为低成本的安全升级方案，但中间相遇攻击使其安全性期望彻底破灭。

3.1 双重DES加密模型

双重DES的加密流程严格遵循“两次加密”逻辑：明文P首先经K1加密得到中间值T，T再经K2加密得到最终密文C，即 C = E_{K2}(E_{K1}(P))。由于DES的加密和解密使用同一算法（仅密钥调度不同），其解密过程为 P = D_{K1}(D_{K2}(C))。

3.2 中间相遇攻击的具象化

针对双重DES的中间相遇攻击步骤如下：

1. 构建加密表：攻击者获取已知明文P（如“HELLOWORLD”的ASCII编码），遍历所有 2^56 个K1，对P执行DES加密得到T值，将 (T, K1) 对存入哈希表。这一过程需消耗 2^56 次加密计算，哈希表存储量约2.3PB。

2. 逆向匹配：获取对应密文C，遍历所有 2^56 个K2，对C执行DES解密得到T'值。

3. 相遇与验证：对每个T'，查询哈希表中是否存在相同T值。若匹配，记录对应的(K1, K2)对；使用第二组(P2, C2)验证，排除因DES的64位分组碰撞导致的伪匹配（碰撞概率约 1/2^64，单次匹配的误判率极低）。

简化小例子（2位密钥双重加密）：假设我们用“移位加密”（密钥是移位位数），明文P=“A”（ASCII码65），密文C=“E”（ASCII码69）。双重加密规则是“先按K1移位，再按K2移位”。

• 可能的密钥：0、1、2、3（共4种，即2^2）

• 建表阶段（K1遍历）：计算A按不同K1移位的结果：K1=0→A(65)，K1=1→B(66)，K1=2→C(67)，K1=3→D(68)。哈希表存为{65:0, 66:1, 67:2, 68:3}。

• 搜索阶段（K2遍历）：计算E按不同K2反向移位（解密）的结果：K2=0→E(69)，K2=1→D(68)，K2=2→C(67)，K2=3→B(66)。

• 匹配验证：发现K2=1时T'=68（D），在哈希表中对应K1=3；用验证明文P2=“B”测试：按K1=3移位→E，再按K2=1移位→F，若密文C2正好是“F”，则(K1=3,K2=1)就是正确密钥对！

3.3 效率的跃升与现实限制

双重DES的理论安全强度为 2^112，但中间相遇攻击将其实际攻击复杂度降至约 2^57 次操作和 2^56 存储。尽管2.3PB的存储在1970年代是“天文数字”（当时最大硬盘容量仅MB级），但在理论上证明了双重DES的安全缺陷——其有效安全性仅比单次DES（2^56）略高，完全达不到“平方级提升”的设计预期。这一结论直接推动了后续三重DES（3DES）的诞生。

4. 攻击的演进与变种

中间相遇攻击并非局限于双重加密场景，经过数十年发展，其思想被拓展到多重加密、哈希函数、流密码等多个领域，衍生出多种优化变种。

4.1 针对三密钥三重加密的攻击

三重加密（3DES）的标准方案为“加密-解密-加密”（EDE）模式，使用三个独立密钥：C = E(K3, D(K2, E(K1, P)))。对于这种三密钥方案，中间相遇攻击依然有效，但需调整攻击策略：

• 攻击思路：将三重加密拆分为“E(K1, P)”和“D(K2, E(K3, C))”两部分，以中间值T = E(K1, P) = D(K2, E(K3, C))为匹配点。

• 具体步骤：遍历所有K1，计算T1 = E(K1, P1)，存储 (T1, K1) 到哈希表（空间复杂度 O(2^n)）；

• 遍历所有K2和K3组合，计算T1' = D(K2, E(K3, C1))（时间复杂度 O(2^(2n))）；

• 匹配T1与T1'，并通过(P2, C2)验证候选密钥对(K1, K2, K3)。

• 复杂度分析：时间复杂度 O(2^(2n))，空间复杂度 O(2^n)。对于3DES（n=56），时间复杂度为 2^112，这一复杂度在当前技术下仍不可行，因此三密钥3DES的有效安全强度为112位（而非168位），在很长一段时间内被视为安全方案。

4.2 时空权衡的进一步优化：TMTO攻击

中间相遇攻击的“空间换时间”思路被进一步优化为“时间-内存权衡攻击”（Time-Memory Trade-Off, TMTO），由Hellman在1980年提出。TMTO通过预计算阶段的“链式存储”减少在线攻击的存储需求，其核心思想是：

• 预计算阶段：生成多个“加密-密钥推导”链，将大量密钥信息压缩存储为“链起点”和“链终点”，而非完整的中间值表。例如，对于DES，一条链可表示为 K0 → E(K0, P) → K1（由E(K0,P)推导）→ E(K1, P) → ... → 链终点。

• 在线攻击阶段：从密文端逆向计算，若结果命中某条链的终点，则回溯该链以找到对应的密钥。

TMTO将存储复杂度从 O(2^n) 降低至 O(2^(n/2))，但代价是增加了预计算时间和在线回溯时间。这种灵活的权衡使其适用于存储资源有限的场景，例如对无线传感器网络中轻量级密码的攻击。

5. 现代密码学中的现实意义与防御

随着密钥长度的增加和新型密码算法的出现，中间相遇攻击的直接威胁有所减弱，但它所代表的分析思想仍深刻影响着现代密码设计与评估。

5.1 攻击的现代局限性

• 对大密钥算法的无效性：对于AES-128（n=128），中间相遇攻击需 2^128 的存储和计算——仅存储量就需约 2^128 * 16字节 ≈ 10^33 PB，这是什么概念？全球数据中心总存储量约100ZB（相当于 10^5 PB），攻击所需存储是这个数的10^28倍，在物理上完全不可实现。

• 工程实现的巨大挑战：即使对于n=64的算法，2^64 个条目（约16EB）的存储管理、数据读写速度等工程问题也难以解决，实际攻击成本极高。

• 对新型加密模式的适应性差：现代分组密码常采用GCM、CCM等认证加密模式，这类模式引入了附加认证数据（AAD）和消息认证码（MAC），增加了中间相遇攻击的碰撞难度和数据需求。

5.2 有效的防御策略

1. 采用大密钥单次加密：这是最直接有效的方案。AES-128/192/256的密钥长度足以抵抗中间相遇攻击，且单次加密的效率远高于多重加密。例如，AES-128的软件实现速度可达每秒数GB，硬件实现更是可达到Tb级，同时具备优异的抗攻击性能。

2. 规范使用三重加密：尽管3DES的有效强度为112位，但在金融、政务等对兼容性要求高的领域仍有应用。需严格遵循“三密钥EDE模式”，避免使用“双密钥3DES”（K1=K3）——这种简化方案会退化为双重DES，完全暴露在中间相遇攻击之下。

3. 强化加密方案的可证明安全性：现代密码设计需通过“可证明安全”框架评估，简单说就是证明“要破解这个方案，必须先解决一个公认很难的数学问题”（比如大整数分解、离散对数）。例如，椭圆曲线密码（ECC）的安全性基于椭圆曲线上的离散对数问题，天然抵抗中间相遇攻击。

4. 限制已知明文对的获取：在实际系统中，通过访问控制、数据加密传输等手段减少攻击者获取P-C对的机会，可提高中间相遇攻击的门槛。

6. 结论与展望

中间相遇攻击不仅是一种具体的密码分析技术，更是密码学史上一次重要的“思维革命”。它深刻揭示了一个核心原则：密码系统的安全性不能仅凭直觉和简单叠加设计，必须经过严格的理论分析和实践检验。

其主要启示在于：

• 安全性是系统性工程：算法设计、密钥管理、加密模式、工程实现等环节相互关联，任何一个环节的疏漏都可能导致整体安全崩溃。

• 分治思想的双面性：分治不仅是构建高效算法的工具，也是破解复杂系统的利器——密码设计者需主动防范此类“拆解式”攻击。

• 资源权衡的动态性：“安全”是相对的，需结合攻击者的时间、空间、数据资源进行评估。随着量子计算、分布式存储等技术的发展，过去“不可行”的攻击可能逐渐具备现实性。

展望未来，后量子密码（PQC）的标准化进程正在加速，以应对量子计算机对传统公钥密码的威胁。在设计格基密码、哈希基密码等后量子算法时，中间相遇攻击所代表的“分治+资源权衡”思想仍是重要的评估维度——例如，格基密码的安全性需抵抗“背包问题的分治攻击”，哈希基签名需防范“多集合碰撞的中间相遇攻击”。

作为密码学的经典分析范式，中间相遇攻击将继续扮演“安全检验者”的角色，推动密码技术在“攻击与防御”的博弈中不断演进，为数字世界构建更可靠的安全基石。