迭代算法求解特征值问题

7 特征值问题的迭代算法

7.1 迭代特征值算法的通用方法论

7.1.1 基本思想

接下来三节的核心主题是大规模特征值问题的降维，其中 $A_{n \times n} = \lambda x_n$，$n$ 较大，且 $A$ 为稀疏或完整矩阵。其数学基础在[29, 55]中已得到充分讨论，并引用了大量相关文献。在本节中，我们采用一种截然不同的方法来探讨特征值问题迭代算法的数学基础。我们将通过几个数值例子来阐明迭代特征值算法的本质。

首先，我们研究对称矩阵的特征值和特征向量的性质。

>>[Q,R]=QR_(randn(8)); d=[1;2;2;3;3;3;4;5]; 矩阵A=Q*diag(d)*A'; %矩阵 A=A' , eig(A) 是 d 。
>>tol = 100*eps;
>>[lambda ,V]= eigSymByQR_(A,tol);>> lambda' % 矩阵A的特征值= 1.0000
2.0000 3.0000 5.0000 4.0000 2.0000 3.0000 3.000 0

特征值和特征向量满足以下方程，参见第1.1.4节：
$$
V’AV= \lambda, V’V= I. \tag{7.1}
$$
这些方程可以很容易地用矩阵 $A$ 计算出的矩阵 $V$ 和 $\lambda$ 进行验证。

>> norm(矩阵V'*矩阵A*矩阵 V-diag(lambda))= 4.5520e-015
>> norm(V'*V- eye(8)) = 1.4221 e-015

方程 $(7.1)$ 也可以针对矩阵 $V$ 的每一列来写，即
$$
V(:,j)’AV(:,j)= \lambda_j, V(:,j)’V(:,j)= 1; j= 1,…,n. \tag{7.2}
$$
并且数值上，方程 $(7.2)$ 验证如下：

>> V(:,4)'*矩阵A*V(:,4)-lambda(4)
= 2.6645e-015>> V(:,4)'*矩阵 A*V(:,5)=-3.3307e-016
>> V(:,4)'*V(:,4)-1.0 = 4.4409 e-016 >> V(:,4)'*V(:,5) = 4.5103 e-017

进一步地，方程 $(7.1)$ 可以写成矩阵 $V$ 的任意列子集的形式，例如，
$$
\begin{bmatrix}
V(:,j)’ \
V(:, k)’
\end{bmatrix}
A
[V(:,j),V(:, k)]
=
\begin{bmatrix}
\lambda_j & 0 \
0 & \lambda_k
\end{bmatrix}
;
\begin{bmatrix}
V(:,j)’ \
V(:, k)’
\end{bmatrix}
[V(:,j),V(:, k)]
=
\begin{bmatrix}
1 & 0 \
0 & 1
\end{bmatrix}. \tag{7.3}
$$
并且在数值上，方程 $(7.3)$ 通过以下计算示例说明：

>>矩阵V45=[V(:,4),V(:,5)];>> 矩阵A45=V45 '*矩阵A*V45= 5.
0000 -0.0000 0.0000 4.0000
>> V45'*V45
= 1.0000 0.0000 0.0000 1.0000

在第6.5节中，我们研究了从给定特征值求解特征向量的问题。该算法是逆迭代。从公式 $(7.1)$ 到 $(7.3)$ 可以看出，如果对应的特征向量已知，则特征值的计算非常简单。但实际上，特征向量是未知的。公式 $(7.1)$–$(7.3)$ 不能直接用于求解特征值。

由矩阵 $A$ 的特征向量张成的子空间是矩阵 $A$ 的不变子空间。这一结论来源于特征向量的定义，因为 $\text{span}(AV(:,j:k)) \subset \text{span}(V(:,j:k))$。特征向量是该不变子空间的一组基（如果是对称的，则为正交基）。如果不变子空间由单个特征向量张成，则它是一维的，其基就是该特征向量。如果不变子空间由多个特征向量张成，则基的选择不是唯一的。例如，由 $V45$ 张成的子空间和由 $V45 \text{randn}(2)$ 张成的子空间完全相同。该矩阵 $A$ 的不变子空间的另一组正交基可通过 $QR_(V45 \text{randn}(2))$ 获得。在接下来的计算中，我们构造同一不变子空间的两组任意正交基，$U45a$ 和 $U45b$。我们看到，$U45a’ A U45a$ 和 $U45b’ A U45b$ 给出了对应于该不变子空间的特征值，并且 $U45a Q45a$ 和 $U45b Q45b$ 均为特征向量。从这个简单例子可以看出，如果我们知道不变子空间 $\text{span}(V(:,4:5))$，则可以通过求解一个 $2 \times 2$ 特征值问题来找到对应于该不变子空间的特征值和特征向量。对于给定矩阵 $A$，整个 $R^8$ 是它的不变空间。如果我们选择 $R^8$ 的一组任意正交基 $U$，我们知道矩阵 $A$ 与 $U’AU$ 具有相同的特征值。但 $U’AU$ 并不能简化其特征值的计算。为了简化特征值的计算，不变子空间的维度应较小。为了找到正确的特征值，应适当选择不变子空间。如果我们想求 $\lambda= 4,5$，则 $\text{span}(V(:,4:5))$ 是最佳选择。任何包含 $\text{span}(V(:,4:5))$ 的更高维空间也同样有效，例如 $\text{span}(V(:,1),V(:,4:5))$。但 $\text{span}(V(:,1:3))$ 不是一个好的选择——此选择对应于 $\lambda= 1,2,3$。实际上，对应于所需特征值的不变子空间仍然是未知的。如下列简单示例所示的特征值计算方法无法直接应用。

>> U45a=QR_(V45*randn(2));>>[s45a ,Q45a]=
eigSymByQR_(U45a'*矩阵A*U45a ,tol) s45a =% 特征值 5.0000 4.0000 Q45a =0.9813 0.1925 -0.1925 0.9813>>U45a*Q45a % 特征向量 ~V45=-0.1533 0.2285 0.5051 -0.2319 -0.0076 -0.2087 -0.1389 0.6552 -0.0049 -0.3722 0.3051 0.5161 0.6068 0.0371 -0.4905 -0.1221
>> U45b=QR_(V45*randn(2));

>>[s45b ,Q45b]=eigSymByQR_(U45b'*矩阵 A*U45b ,tol) s45b =% 仍然是特征值 4.0000 5.0000 Q45b =0.8217 -0.5699 0.5699 0.8217>>U45b*Q45b % 仍然是特征向量 ~V45=-0.2285 0.1533 0.2319 -0.5051 0.2087 0.0076 -0.6552 0.1389 0.3722 0.0049 -0.5161 -0.3051 -0.0371 -0.6068 0.1221 0.4905

在上述计算中，如果 $U45a$ 和 $U45b$ 的张成空间不是对应于 $\lambda= 4,5$ 的矩阵 $A$ 的不变子空间，则可以预期 $U45a’ A U45a$ 和 $U45b’ A U45b$ 的特征值不会是 $\lambda= 4,5$。$\text{span}(U45)$ 与 $\text{span}(V45)$ 的差异越大，$U45’ A U45$ 的特征值与 $\lambda= 4,5$ 的差异也越大。以下计算支持这一结论。

>>v1=randn(2); v2a=randn(6,2); v2b=0.01*v2a; % 张成空间 ( 
U45a ) 与 张成空间 ( V45 ) 存在较大偏差>>[U45a ,R]=
QR_(V45*v1+[V(:,1:3),V(:,6:8)]*v2a); % 张成空间 ( U45b ) 与 
张成空间 ( V45 ) 偏差较小>>[U45b ,R]=QR_(V45*v1+[ V(:,1:3),V(:,6:8)]*v2b);>>[s45a ,Q45a]=
eigSymByQR_(U45a'*矩阵A*U45a ,tol) s45a =% 与 lambda 存在较大差异=4,5 3.0869 2.8132 Q45a =0.9720
0.2348 -0.2348 0.9720>>[s45b ,Q45b]=
eigSymByQR_(U45b'*矩阵A*U45b ,tol) s45b =% 与 lambda 差异较小=4,5 3.9995 4.9992 Q45b =0.9994 -0.0341 0.0341 0.9994

关于特征值的观察，我们对对称矩阵得出的结论同样适用于非对称矩阵。对于非对称矩阵，特征向量不是正交的，但舒尔向量是正交的。为了简洁起见，我们将通过一个简单的非对称矩阵来演示这些观察结果。

>>矩阵A(2:8,1)=-A(2:8,1); A(1:7,8)=-A(1:7,8); % 为了使矩阵A不对称>>v1=randn(3); v2a=randn(5,3); v2b=
v2a*0.01; % 为了创建正交基

首先，我们通过使用特征值和特征向量来检查观测结果。

>>[Lambda ,V]=eigUnsymByQR_(矩阵A,tol,'长格式'); % 特征值和特征向量>> Lambda= 3.
5756 0.8386 -0.8386 3.5756

1.4288 0 % 实数特征值：3 = lambda (1) 按顺序排列 3.8753 0 2 .7723 0 .3004 % 复特征值:5 ,6= lambda (3 ,4) 有序的 -0.3004 2.7723 2.0001 0 3.0000 0>>[U356 ,R]=QR_([V(:,3),V(:,5:6)]*v1); % 张成空间 ( U356 )=张成空间 ( V (: ,3) , V (: ,5:6))>>[L356 ,Q356]=eigUnsymByQR_(U356'*矩阵A*U356 ,tol ,'长格式');>> L356
= 1.4288 0 % 实数特征值 2.7723 0.3004 % 复特征值 -0.3004 2.7723>>V356=U356*Q356; % 特征向量 , ~[
V (: ,3) , V (: ,5:6)]>>范数(矩阵A*V356 -V356*[L356(1,:),0;[0;0],L356(2:3,:)])= 1.2319e-014 % 精确对应于
张成空间 ( U356 )=张成空间 ( V (: ,3) , V (: ,5:6)) % 张成空间 ( U356a ) 远离张成空间 ( V (: ,3) , V (: ,5:6))>>[ U356a ,R]=QR_([V(:,3),V(:,5:6)]*v1+[V(:,1:2),V(:,4),V(:,7:8)]*v2a);>>[L356a ,Q356a]= eigUnsymByQR_(U356a'*矩阵A*U356a ,tol ,'长格式');>> L356a % 与Lambda差异较大= 3.7662
1.8688 2.6338>> V356a=U356a*Q356a;>>范数(矩阵A*V356a -V356a*diag(L356a))= 0.8577 % L356a ,
V356a 远离特征值（特征向量） % 张成空间 ( U356b ) 接近张成空间 ( V (: ,3) , V (: ,5:6))>>[U356b ,R]=QR_([
V(:,3),V(:,5:6)]*v1+[V(:,1:2),V(:,4),V(:,7:8)]*v2b);>>[L356b ,Q356b]=eigUnsymByQR_(U356b'*矩阵
A*U356b ,tol ,'长格式');>> L356b % 与Lambda差异较小= 1.4310 0 2.7735 0.3105 -0.3105 2.7735>> V356b=U356b*Q356b;>>范数(矩阵A*V356b -V356b*[L356b(1,:),0;[0;0],L356b(2:3,:)356=)= 0.0274 % L356b , V356b 接近特征值（特征向量）

接下来，我们通过使用特征值和舒尔向量来验证这些观测结果。为了在之前使用特征向量的计算中获得相同的由 $(V(:,3),V(:,5:6))$ 张成的不变子空间，我们需要对通过 $W$ 计算得到的舒尔向量 $eigUnsymByQR_$ 进行重排序，使得 $(W(:,1:3))= \text{span}(V(:,3),V(:,5:6))$。有关通过特征值重排序计算不变子空间的内容，请参见第6.6节。

>>[S,W]= eigUnsymByQR_(矩阵A,100*eps ,'short' ); % 拟上三角矩阵和舒尔向量>>[S,W]=
reorderSchur_(S,W,[1,3,4],100*eps);>>S % 重排 S , W 。W (: ,1:3) => i n v a r i a n t 子空间 of 矩
阵A to lambda (1 ,3 ,4)= 1.4288 0.3711 -0.0375 0.6799 0.7143 0.0290 -0.0024 0.0000 0.0000 2.8585 0.3628 0.9125 0.0677 -0.3549 0.0059 0.0000 -0.0000 -0.2693 2.6861 -0.6385 -0.3287 -0.3878 0.0062 -0.0000 0.0000 -0.0000 0.0000 3.9706 -1.5496 -0.1060 0.0022 -0.0000 0.0000 0.0000 -0.0000 0.0000 3.1806 -0.0769 -0.0072 0.0000 0.0000 0.0000 0.0000 -0.0000 -0.0000 3.8753 0.0043 -0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0000 0.0000 2.0001 0.0000 0 0 0 0 0 0 0 3.0000

>>[U356 ,R]=QR_(W(:,1:3)*v1); % 张成空间 ( U356 )=张成空间 ( W (: ,1:3))>>[S356 ,Q356]= eigUnsymByQR_(U356'*矩阵A*U356 ,tol ,'short');>> S356= 1.4288 -0.3470 0.1369 % 实数 特征值 (1 ,1) 0 2.7841 -0.4133 % 复数 特征 值 (2:3 ,2:3) 0.0000 0.2187 2.7605>> W356=U356*Q356; % 舒尔向量 ，~ W (: ,
1:3)>>范数(矩阵A*W356 -W356*S356)= 3.7679e-015 % 精确对应 张成空间 ( U356 )=张成空间 ( W (: ,1:3)) % 张成空间 ( U356a ) 远离 张成空间 ( W (: ,1:3))>>[U356a ,R]=QR_(W(:,1:3)*v1+W(:,4:8)*v2a);>>[S356a ,
Q356a]=eigUnsymByQR_(U356a'*矩阵A*U356a ,tol ,'short');>> S356a % 与 S (1:3 ,1:3) 差异较大= 1.
5621 -0.1915 -0.5041 0 3.8109 0.5972 0 0 2.7266>> W356a=U356a*Q356a;>>范数(矩阵A*W356a -
W356a*S356a)= 1.4947 % S356a , W356a 远离 特征值 和 舒尔向量 % 张成空间 ( U356b ) 接近 张成空间 ( W (: , 1:3))>>[U356b ,R]=QR_(W(:,1:3)*v1+W(:,4:8)*v2b);>>[S356b ,Q356b]=eigUnsymByQR_(U356b'*矩阵
A*U356b ,tol ,'short');>> S356b % 与 S (1:3 ,1:3) 差异较小= 1.4257 -0.3570 0.0769 0 2.8013 -0.4273 0
0.2276 2.7245>> W356b=U356b*Q356b;>>范数(矩阵A*W356b -W356b*S356b)= 0.0532 % S356b , W356b 接近 特征值 和 舒尔向量

利用上述通过 $QR_(W(:,1:3)*v1)$ 计算得到的正交列 $U356$，我们可以构造一个满足 $U(:,1:3)= U356$ 的正交矩阵 $U$。这样的 $U$ 并不唯一，一种简单的方法是使用 $orthogonal_.m$ 来生成它。

>>矩阵U=矩阵U356;>>对于 j=4:8 矩阵U=[矩阵U,正交_(矩阵 U,randn(8,1))]; 结束 >> norm(U(:,1:3)-U356)
= 0>> norm(U'
*U-eye(8))= 4.8070e-016

这样的 $U$ 具有一个有用的性质，可以对 $U’AU$ 进行缩并。

>> B=U'*矩阵A*U
B= 1.9841 0.0644 0.6914 -0.2966 0.1386 -0.3853 0.7054 -0.2179 0.7073 2.7246 -0.0906 -0.5712 - 0.3405 0.5694 -0.9212 -0.1515 0.4287 -0.3279 2.2647 -0.1010 0.2250 0.0304 0.2309 0.2208 0.0000 - 0.0000 -0.0000 3.8154 -0.0109 -0.1406 -0.3894 0.5016 0.0000 -0.0000 0.0000 -0.0030 3.3436 0.2534 - 0.0945 0.6809 0.0000 0.0000 0.0000 -0.6655 -0.3310 2.4723 -0.4206 -0.0175 0.0000 0.0000 0.0000 0.2758 0.6316 0.0587 3.1231 1.2010 0.0000 -0.0000 0.0000 0.1448 0.2791 0.7715 -0.1094 3.2722
>> norm(B(4:8,1:3))= 3.
4077e-015

从上述讨论中可以看出，如果我们能找到一个子空间，该子空间能准确包含所求特征值对应的不变子空间，那么就可以通过求解一个规模较小的特征值问题来精确计算矩阵的特征值。

代数上，到目前为止讨论的思想可以通过正交投影方法简洁地表示，另见第5.3节。给定一个列正交矩阵 $U \in R^{n \times m}$，如果矩阵 $A$ 的特征向量 $v$ 可以表示为 $v = Uy$，则 $Av = AUy = \lambda v = \lambda Uy$。由于 $U’U = I$，有 $(U’AU)y = \lambda y$。如果 $v$ 不能表示为 $Uy$，则 $AUy - \lambda Uy , 0$。为了确定 $(\lambda, y)$，我们假设非零残差在 $U$ 上的投影为零，即 $(U’AU)y = \lambda y$。该对 $(\lambda,y)$ 称为瑞利值和瑞利向量，它是小规模特征值问题 $(U’AU)y = \lambda y$ 的特征值和特征向量。该方法的效率和精度取决于所选择的 $U$。在迭代算法中，通过采用一系列数值技术使 $U$ 逐步逼近矩阵 $A$ 的期望的不变子空间，其中一些技术将在下文简要讨论。

7.1.2 近似主导不变子空间的两种方法

给定矩阵 $Q \in R^{n \times m}$，根据第6.3节的讨论可知，当 $k$ 较大时，$A^kQ$ 近似表示矩阵 $A$ 对应于主导特征值的不变子空间。如果 $Q$ 在主导不变子空间中有较大的分量，则即使 $k$ 较小，$A^kQ$ 也能近似表示该子空间。如果 $Q$ 恰好表示矩阵 $A$ 的一个不变子空间，则可直接用于简化特征值的计算，如上述示例所示。通过对 $A^kQ$ 进行 QR 分解，可以得到其张成子空间的一组正交基 $V$。如果 $Q$ 仅有一列，则 $A^kQ$ 的 QR 分解就是对 $A^kQ$ 的归一化。所得矩阵 $V’AV$ 通常是一个满矩阵。使用 $A^kQ$ 来近似主导子空间的方法即为第6.3节和第7.2节中介绍的幂迭代和子空间迭代算法。

给定一个向量 $q \in R^n$，Krylov 子空间 $K(A, q, m) = \text{span} { q, Aq, A^2q, …, A^{m-1}q }$ 通常比 $A^kQ$ 更好地表示矩阵 $A$ 的主子空间，因为前者由矩阵 $A$ 的完整 $(m-1)$ 阶多项式构成空间，而后者仅由单项 $A^k$ 构成空间。$K(A, q, m)$ 的正交基 $V$ 通过逐步构造形成，即对称矩阵使用 $QTQtByLanczos_.m$，非对称矩阵使用 $QHQtByArnoldi_.m$。所得的 $V’AV$ 为对称三对角或上 Hessenberg 形式。分别参见第3.6.3节和第3.5.3节。使用 $K(A, q, m)$ 来逼近主子空间的算法，是对称矩阵情况下的第7.3节中的兰索斯算法，以及非对称矩阵情况下的第7.4节中的阿诺尔迪算法。

7.1.3 移位与逆变换以近似非主导不变子空间

上述迭代算法在收敛到特征值的最大模时非常有效，因为主导不变子空间可以通过矩阵 $A^kQ$ 或 $K(A, q, m)$ 得到最佳逼近。如果我们需要找到位于矩阵谱内部的其他特征值，则这些迭代算法可能需要大量迭代次数才能收敛到期望的特征值。在这种情况下，我们可以尝试将迭代算法应用于变换后的特征值问题，
$$
(A -\sigma I)^{-1} w= \theta w. \tag{7.4}
$$
该变换后的特征值问题的特征对 $(\theta,w)$ 与原特征值问题 $Av= \lambda v$ 的特征对 $(\lambda, v)$ 之间的关系为
$$
\theta=\frac{1}{\lambda -\sigma}, w= v. \tag{7.5}
$$
如果所求特征值 $\lambda$ 接近于 $\sigma$，$\theta$ 则是 $(A-\sigma I)^{-1}$ 的模最大特征值。将迭代算法应用于方程 $(7.4)$ 可实现快速收敛。

在子空间迭代中，不变子空间由 $(A-\sigma I)^{-k} Q$ 逼近。在兰索斯或阿诺尔迪迭代中，不变子空间由 $K((A -\sigma I)^{-1},q,m)$ 逼近。在这两种情况下，我们都需要求解线性方程 $(A -\sigma I)^{-1} b$，有关算法参见第4章和5章。在7.2–7.4节中，提供了数值例子来演示该方法的使用。

7.1.4 更好地逼近不变子空间

在迭代开始时，不变子空间由 $C^kQ$ 或 $K(C,q, m)$ 逼近，其中 $C=A$ 或 $C=(A -\sigma I)^{-1}$。如果已知关于目标不变子空间的任何信息，则应构造初始的 $Q$ 或 $q$ 以包含足够多的该子空间分量。如果没有任何信息可用，则 $Q$ 或 $q$ 可以随机生成。在后续迭代中，不变子空间仍以相同形式 $C^kQ$ 或 $K(C,q, m)$ 逼近。然而，通过计算 $(U’CU)v= \lambda v$ 的特征值得到了更多信息，我们可以利用更优的 $Q$ 或 $q$ 来启动每次迭代。根据已有信息，可单独或联合应用三种技术： 1. 非收敛且不需要谱的滤波。2. 已收敛且不需要谱的清除。3. 已收敛且所需谱的锁定。

这些技术将在第7.3和7.4节的兰索斯和阿诺尔迪算法中更详细地讨论。

7.2 求解 $Ax = \lambda x$ 的幂迭代与子空间迭代

幂迭代和子空间迭代的公式在第6.3节中讨论。如第7.1节指出，在 $(U’AU) y= \lambda y$ 中，$U$ 是由矩阵 $A^kQ$ 张成的子空间的一组正交基，其中 $Q$ 是用户输入或随机生成的矩阵。如果 $Q$ 的列数仅为一，则该算法即为幂迭代，否则为子空间迭代。本节重点介绍 $eigBySubspace_.m$ 的代码实现，并通过几个数值例子演示 $eigBySubspace_.m$ 的应用。

算法 7.1
$AV= V\lambda$ 通过子空间迭代。

函数 [lambda ,V]=eigBySubspace_(矩阵A,算法 , Q,tol,nv,lambda ,矩阵V)[m,n]= size_(矩阵A); nlambda = 0; 范数A =范数 (Ay_(矩阵A,ones(m,1))); eqsALGO ='mtimes'; eigALGO = ' eigUnsymByQR_'; 如果 (length(算法)>=1&& ~isempty(算法{1})) sigma =算法 {1}; 结束 如果 (length(算法)>=2&& [isempty(算法{2})) eqsALGO =算法{2}; 结束 如果 (length(算法)>=3&& ~isempty(算法{3})) eigALGO =算法{3}; 结束

如果 (~isempty(nv) && strcmp(nv{1},'n'))
l1=nv{2}; l2= nv{3} 如果 (strcmp(eigALGO ,'eigSymByQR_')) [v1,v2]= veig_(矩阵A,l1,l2); % 完整 矩阵A=A'!!
else v1= -realmax; v2= realmax; end elseif (~isempty(nv) && strcmp(nv{1},'v'))
v1=nv{2}; v2=nv{3};
如果 (strcmp(eigALGO ,'eigSymByQR_')) [l1,l2]= neig_(矩阵A,[,2]=); % 完整 矩阵A=A'!!
否则 l1= 1; l2=n; 结束 否则 l1=n; l2= n; v1=-realmax; v2= realmax; 结束 l12= l2 - l1+ 1; 如果 (~exist('Q','var') || isempty(Q)) Q = randn(m,min([fix(n/2),2*l12 ,l12+8])); 结束 如果 (exist('sigma','var')) A = A_(A,sigma ,eqsALGO); 结束 AQ= Ay_(A,Q); nq0= size(Q,2); tol1= 1000.0*tol; while(nlambda<l12 && length(lambda)<n) nq0=min(nq0 ,n-size(矩阵V,2)); nq = size(AQ ,2); 如果 (nq < nq0) AQ =[AQ, randn(m,nq0 -nq)]; 结束 如果 (size(矩阵V,2) > 0) AQ =AQ - 矩阵V*(矩阵V'*AQ); 结束 % 定义：对 A ~=A' 不适用 如果 (size(AQ ,2)==1) r =范数(AQ); Q = AQ/r; 否则 [Q,r]=
QR_(AQ,'householder',0,tol ,'short'); 结束 AQ= Ay_(A,Q); 西塔 = Q'*AQ; j = 0; k = 1; l = size(西塔 ,
1); [ml,nl]= size(lambda); 如果 (size(AQ ,2) > 1) 如果(strcmp(eigALGO ,'eigSymByQR_')) [西塔 ,S]= eigSymByQR_(西塔 ,tol ,'long'); 否则 [西塔 ,S]=eigUnsymByQR_(西塔 ,tol ,'long'); 结束 Q = Q*S; AQ = Ay_(A,Q); % 用于误差检查的 AQ 结束 while k <=l % 检查收敛性 如果 (

k == l || 西塔(k,2) == 0) % 实数
如果 (范数(AQ(:,k) - Q(:,k) * 西塔(k,1)) <= tol1 * 范数A)
如果 (exist(‘sigma’,’var’)) 西塔(k) = sigma + 1.0 / 西塔(k,1); 结束
如果 (nl ~= 2) lambda = [lambda; 西塔(k,1)]; 否则 lambda = [lambda; [西塔(k,1), 0]]; 结束
矩阵V = [矩阵V, Q(:,k)];
如果 (v1 <= 西塔(k) && 西塔(k) <= v2) nlambda = nlambda + 1; 结束
否则
j = j + 1;
如果 (j < k) AQ(:,j) = AQ(:,k); 结束
结束
k = k + 1;
否则 % 复数
如果 (范数(AQ(:,k:k+1) - Q(:,k:k+1) * 西塔(k:k+1,:)) < tol1 * 范数A)
如果 (exist(‘sigma’,’var’))
西塔3 = 西塔(k,1) * 西塔(k,1) + 西塔(k,2) * 西塔(k,2);
西塔(k,1) = sigma + 西塔(k,1) / 西塔3;
西塔(k,2) = -西塔(k,2) / 西塔3;
西塔(k+1,1) = -西塔(k,2);
西塔(k+1,2) = 西塔(k,1);
结束
如果 (nl == 1) lambda = [lambda, zeros(ml, 1)]; 结束
lambda = [lambda; 西塔(k:k+1,:)];
矩阵V = [矩阵V, Q(:,k:k+1)];
nlambda = nlambda + 2;
否则
j = j + 1;
如果 (j < k) AQ(:,j:j+1) = AQ(:,k:k+1); 结束
j = j + 1;
结束
k = k + 2;
结束
结束
如果 (j < size(矩阵A矩阵Q, 2)) 矩阵A矩阵Q = 矩阵A矩阵Q(:,1:j); 结束
结束

可选的第二个输入参数 `algo` 是一个元胞数组，用于定义偏移量（`sigma`）、求解 $(A - \sigma I)^{-1}$ 所用的算法以及约化特征值问题所用的算法。例如，`algo={2.1,'LDLt_','eigSymByQR_'}`。如果第三个输入参数 `Q` 是一个向量，则 `eigBySubspace_.m` 实现幂迭代算法。如果 `Q` 是一个具有多于一列的矩阵，则 `eigBySubspace_.m` 实现子空间迭代算法。可选的第五个参数 `nv` 定义了由 `eigBySubspace_.m` 所求特征值的范围。例如，`nv={'n',2,5}` 指示 `eigBySubspace_.m` 计算第2到第5个特征值。而 `nv={'v',2.0,5.0}` 则指示 `eigBySubspace_.m` 计算介于2.0到5.0之间的特征值。

`eigBySubspace_.m` 使用 `veig_.m` 或 `neig_.m` 来确定所求特征值的范围。由于 `veig_.m` 和 `neig_.m` 仅适用于对称矩阵，并且仅针对完整对称矩阵实现，因此第五个输入参数 `nv` 不用于其他类型的矩阵。

通过以下示例演示了 `eigBySubspace_.m` 的使用。第一个示例是一个对称矩阵。

[Q,R]=QR_(randn(8)); d=[1;2;2;3;3;3;4;5]; 矩阵A=Q diag(d) Q’; % eig ( 矩阵A) 是 d 。
q = randn(8,1); tol = 100 eps;
[lambda,V]=eigBySubspace_(矩阵A,{},q,tol);>> lambda= 5.0000>> V’= 0.1387 0.4871 0.2780 -0.1950 0.4368 -0.1199 -0.5749 0.3040
norm(A V-V*lambda)=1.2570e-010 % 正确的特征值和特征向量

由于5是模最大的特征值，幂迭代将收敛到5。如果我们从不同的 `q` 开始，很可能得到相同的（更准确地说，数值上接近的） $\lambda= 5$ 和相同的 $V$。

为了获得 $\lambda= 4$ 及其对应的特征向量，我们必须将 $(\lambda= 5,V)$ 作为输入参数传递给 `eqsSubSpace_.m`。在每次迭代中，对应于 $\lambda= 5$ 的特征向量被收缩。

[lambda ,V]=eigBySubspace_(矩阵A,{},q,tol,{},lambda ,矩阵V);>> lambda ‘
= 5.0000 4.0000>> V’= -0.1387 0.0389 -0.3434 0.7924 0.1005 -0.4871 0.3744 -0.2070 -0.1627 0.3248 -0.2780 0.0192 0.0479 -0.3088 0.5333 0.1950 -0.4135 -0.7287 -0.0665 0.1092 -0.4368 0.3592 -0.1608 0.0313 -0.6331 0.1199 -0.1428 -0.1489 -0.3878 -0.4180 0.5749 0.4909 0.1733 0.1675 0.0984 -0.3040 -0.5446 0.4773 0.2578 -0.0529

为了在较少的迭代次数内计算谱中部的特征值，我们可以使用输入参数 `algo` 设置一个偏移，然后使用逆向子空间迭代。例如，如果我们想要计算 $\lambda(2:4)=[2; 2; 3]$，我们可以将偏移设置为 $2.1$。因为 $2.1$ 接近 $\lambda= 2$，$\lambda= 2$ 首先收敛。

[lambda ,V]=eigBySubspace_(矩阵A,{2.1,’LDLt_’},randn(8,1),tol ,{‘n’,2,4});>> lambda ‘= 2.0000 2.0000 3.0000>> V’
= 0.0425 0.1670 -0.5113 -0.3604 -0.4414 -0.0094 -0.5002 -0.3660 -0.4263 -0.1451 -0.2212 0.2424 0.2173 -0.7833 -0.1385 -0.0982 0.1476 0.3464 0.5211 0.1966 -0.6086 -0.3997 0.0779 -0.1086

我们可以将 `eqsSubSpace_.m` 应用于非对称矩阵。作为另一个示例，我们从上面示例中使用的 $A$ 创建一个非对称矩阵，方法如下。

矩阵A =矩阵A-2 tril(矩阵A,-1); % 矩阵A=-A’>>[lambda,矩阵V]=eigBySubspace_(
矩阵A,{[],[],’eigUnsymByQR_’},randn(8,2),tol);>> lambda
= 2.9366 1.8483 -1.8483 2.9366
V’ % V 可以随 randn (8 ,2) 改变，但 span ( V) 不会改变。
= 0.0375 -0.4916 -0.1526 0.0911 -0.2300 -0.0363 0.2190 0.3916 0.0523 0.3211 -0.3412 0.1672 -0.1387 0.1430 0.4184 - 0.0704
norm(A V-V*lambda)=1.7373e-010 % 正确的特征值和特征向量

该矩阵可以是带状或稀疏的。例如，我们从上述示例中的矩阵 $A$ 创建以下带状矩阵。输入 `{‘band’,{B,2,1,8,8}}` 提供了带状矩阵的完整信息。

矩阵A=矩阵A-tril(A,-3)-triu(A,2);
B=full2band_(矩阵A,2,1) B =
0 0 2.7769 0.3326 0 -0.3326 2.7682 0.9371 0.1860 -0.9371 2.3847 -0.0222 0.5454 0.0222 2.9486 -0.4827 0.0258 0.4827 3.2478 0.0235 -0.2614 -0.0235 2.4268 -0.0853 0.4549 0.0853 3.4499 -1.0631 0.1299 1.0631 2.9971 0
[lambda ,矩阵V]=eigBySubspace_({’band’,{B,2,1,8,8}},{[],[],’eigUnsymByQR_’},…
randn(8,2),tol);
lambda= 3.2192 1.0388 -1.0388 3.2192
V’ % V 可以用 randn(8,2) 改变，但 span(V) 不变。
= -0.0000 0.0000 0.0000 -0.0004 -0.0008 -0.0384 0.0460 0.6968 -0.0000 -0.0000 0.0000 -0.0005 0.0011 -0.0256 0.7063 0.1068
norm(A V-V lambda)=1.7824e-010 % 正确的特征值和特征向量

以下示例展示了如何对非对称带状矩阵使用位移算法。

[lambda ,矩阵V]=eigBySubspace_({’带状’,{B,2,1,8,8}},{2.8,’LU_’,’eigUnsymByQR_’},…
randn(8,2),tol);
lambda= 2.7919>>V’ %+/- V 不随 randn(8,2) 变化。=-0.9375 -0.0424 -0.3338 0.0610 -0.0435 -0.0429 0.0085 -0.0168
norm(A V-V lambda )=6.5284e-013 % 正确的特征值和特征向量

需要注意的是，对于非对称矩阵，`eigBySubspace_.m` 中未实现特征值偏移。为了实现 deflation，我们必须使用舒尔向量而不是特征向量。

## 7.3 对称矩阵 $Ax = \lambda x$ 的 Lanczos 迭代

### 7.3.1 基本 Lanczos 算法

正交基 $U$ 的 Krylov 子空间 $K(A,q,m)=\text{span} \{ q, Aq, A^2q, ..., A^{m-1}q \}$ 可通过 `QTQtByLanczos_.m` 构造。根据矩阵 $V$ 的构造，矩阵 $V$ 和一个对称三对角矩阵 $T$ 满足以下重要关系，见第3.6.3节：
$$
AU(:,1: m)= U(:,1: m)T(1: m,1: m)+ T(m+ 1,m)U(:,m+ 1)I(m,:), \tag{7.6a}
$$
$$
U(:,1: m)'U(:,1: m)= I, \tag{7.6b}
$$
$$
U(:,1: m)'U(:,m+ 1)= 0. \tag{7.6c}
$$
假设矩阵 $A$ 的一个特征对为 $(\lambda, v)$，其中 $v$ 可近似表示为 $v=U(:,1 : m)u$。为了确定两个未知量 $(\lambda,u)$，我们引入以下伽辽金条件：
$$
U(:,1: m)'y= U(:,1: m)'(AU(:,1: m)u- \lambda U(:,1: m)u)= 0. \tag{7.7}
$$
考虑方程 $(7.6)$，上述伽辽金条件可简化为
$$
T(1: m,1: m)u= \lambda u. \tag{7.8}
$$
由方程 $(7.8)$ 可知，$(\lambda,u)$ 可通过任意用于对称三对角矩阵的特征值算法求得，例如 `eigSymByQR_.m`、`eigTridByDet_.m` 或 `eigTridByR1U_.m`，参见第6.4节和6.7节。一旦 $(\lambda,u)$ 确定，残差 $r$ 即可数值计算得到。
$$
r= Av- \lambda v= AU(:,1: m)u- \lambda U(:,1: m)u =(U(:,1: m)T(1: m,1: m)+ T(m+ 1,m)U(:,m+ 1)I(m,:))u- \lambda U(:,1: m)u
= U(:,1: m)(T(1: m,1: m)u- \lambda u)+ T(m+ 1,m)u(m)U(:,m+ 1) = T(m+ 1,m)u(m)U(:,m+ 1).
\tag{7.9}
$$
由公式 $(7.9)$ 可知，残差（即 $(\lambda, U(:,1 : m)u)$ 作为矩阵 $A$ 的特征对的误差度量）位于 $U(:,m+ 1)$ 的方向上。其大小 $\|r\|_2$ 为 $\|T(m+ 1, m)u(m)\|$。$\|T(m+ 1, m)u(m)\|$ 为特征对的收敛性提供了一个有效的检验。只有当 $\|T(m+ 1, m)u(m)\|$ 足够小时，我们才构造特征向量 $U(:,1 : m)u$。较小的 $\|T(m+ 1, m)u(m)\|$ 表明 $T(m+ 1, m)$ 或 $u(m)$ 很小。如果 $T(m+ 1, m)$ 很小，则 $K(A, q, m)$ 构成了矩阵 $A$ 的一个精确的 $m$ 维不变子空间。$U(:,1 : m)'AU(:,1 : m)$ 的全部 $m$ 个特征值也是矩阵 $A$ 的特征值。如果 $T(m+ 1, m)$ 并不小但 $u(m)$ 很小，则 $K(A, q, m)$ 包含矩阵 $A$ 的一个一维不变子空间，且 $\lambda=u'Au$ 是一个特征值。参见第 7.1.1 节的讨论。

### 7.3.2 $U$ 的正交性

上一小节的简要讨论是经典 Lanczos 算法。其正确实现依赖于两个隐含条件，即方程 $(7.6b)$ 和 $(7.6c)$，我们用它得到了方程 $(7.8)$。这两个条件即 $U$ 各列之间的正交性。

由方程 $(7.6)$，我们可以计算以下内容：
$$
U(:,1: j)'U(:,j+ 1)= U(:,1: j)'(AU(:, i)- T(j,j - 1)U(:,j - 1)- T(j,j)U(:,j)) T(j+ 1,j) .
\tag{7.10}
$$
如果 $\|T( j+ 1, j)\|$ 很小，则即使 $U(:,1 : j)$ 自身的正交性是准确的，$U(:,1 : j)$ 与 $U(:,j+ 1)$ 之间也可能发生显著的正交性丢失。当 $U(:,1:j)$ 接近矩阵 $A$ 的不变子空间时，会出现较小的 $\|T( j+ 1, j)\|$，也就是说，当 $T(1 : j, 1 : j)$ 的所有特征值都接近于 $A$ 的特征值时。

由方程 $(7.9)$，我们可以计算出以下内容：
$$
v'U(:,j+ 1)= v'(Av- \lambda v) T(j+ 1,j)u(j) .
\tag{7.11}
$$
如果 $\|T(j+ 1,j)\|$ 不很小，但 $v$ 是已收敛的瑞利向量，则 $\|u(j)\|$ 必须很小。公式 $(7.11)$ 告诉我们，一个很小的 $\|u(j)\|$ 意味着 $v'U(:,j+ 1)$ 可能显著地偏离零。但 $v=U(:,1:j)u$，这意味着 $U(:,1:j)'U(:,j+ 1)$ 可能显著地偏离零。

在公式 $(7.10)$ 和 $(7.11)$ 中，$j$ 可以是 $1$ 到 $m$ 之间的任意数，其中 $m$ 是 Lanczos 步数的极限值。

如果不处理正交性丢失问题，已收敛的特征对 $(\lambda,u)$ 的重复副本将很快出现在三对角矩阵 $T(1 : m,1 : m)$ 中。这是因为新计算的矩阵 $U$ 的列在已收敛的 Ritz 向量中具有不可忽略的分量。

有四种不同的方法可以弥补正交性丢失问题。

**半重新正交化** 图7.1 说明了 Lanczos 步骤中的三个向量。如果角度 $\theta$ 较小，则 $AU(:, j)$ 在 $\text{span} (U(:, j -1), U(:, j))$ 中具有显著分量；换句话说，$AU(:, j)$ 接近不变的。为了获得更高的精度，在这种情况下将 $U(:,j+ 1)$ 对 $U(:,1 : j - 1)$ 进行正交化。如果标记为 $AU(:, j)$ 和 $T_{j -1, j} U(:, j - 1) + T_{j , j}U(:, j)$ 的两个向量是随机选取的，则采用 $\theta= 45^\circ$ 将有 50% 的概率进行重新正交化。$\theta= 45^\circ$ 对应于在 `QTQtByLanczos_.m` 中将 `eta=0.5*sqrt(2.0)` 设为。对于给定的对称矩阵 $A$ 和初始向量 $q$，将 `eta=0.5*sqrt(2.0)` 设为并不意味着在一半的 Lanczos 步骤中执行重新正交化。使用 `eta=0.5*sqrt(2.0)` 作为判据的研究见 [18]。

![示意图0](https://c.csdnimg.cn/blog_illustration/2025-10-14/71ea58130014e5e66fdfc1b976e9adb0.png)
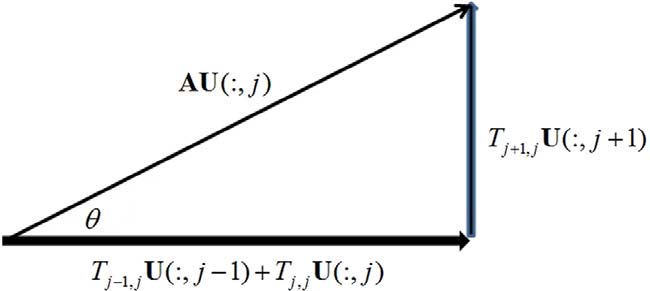
Lanczos 步骤中的三个向量。

**完全重新正交化** 将新计算的 $U$ 的列与 $U$ 的所有先前列进行重新正交化。首先通过 Lanczos 三项递推公式，即方程 $(7.6)$，计算 $U(:,j+ 1)$。然后根据 $U(:,j+1)=U(:,j+1) -U(:,1 : j) (U(:,1 : j)'U(:,1 : j+ 1))$。随着 $j$ 的增长，计算量增加是不可接受的。在 `QTQtByLancos_.m` 中，设置 `eta=realmax` 对应此方案。

**无正交化** 参见 [15]。在此方案中，仅根据兰索斯三项递推公式显式执行 $U(:,j - 1)$ 与 $U(:, j)$，$j= 2, ..., m+ 1$ 之间的正交化。在 `QTQtByLanczos_.m` 中，设置 `eta=0` 对应于局部正交化。当 $U(:,1 : j)'U(:,1 : j),I(1 : j,1 : j)$ 时，$U(:,1 : j)'AU(:,1 : j)$ 中会出现重复的特征对。

为了说明，我们来看以下简单示例。

[Q,R]=QR_(randn(8))；d=[1；2；2；3；3；3；4；5]；矩阵A=Q diag(d) A’；% 矩阵A =A’ ，eig(A) 是 d 。
[lambda ,V]= eigSymByQR_(A,100*eps);>>lambda ’ % 矩阵A的特征值= 5.0000 4.0000 3.0000 2.0000 1.0000 3.0000 2.0000 3.0000

我们选择一个初始向量 $q$，它属于对应于 $\lambda=3,1,3$ 的二维不变子空间。正如预期的那样，$T_{32} \approx 0$。由于仅进行了局部正交化，$U(:,3: 4)'U(:,1: 2), 0$。因此，方程 $(7.6)$ 不再成立。

q=[V(:,3),V(:,5:6)] randn(3,1); % q 属于 张成空间 ([矩阵V (: ,3) , 矩阵V (: ,5:6)])
[U,T3]= QTQtByLanczos_(矩阵A,1,4,q); % 设置 eta =0在 QTQtByLanczos_ . m 中
T=band2full_(T3,1,1,5,5) % 注意 T (3 ,2)=1.7644 e -015=8 eps T= 1.7766 0.9747 0 0 0 0.9747 2.2234 0.0000 0 0 0 0.0000 4.1254 1.0298 0 0 0 1.0298 3.1650 1.0655 0 0 0 1.0655 0
矩阵V(:,1:4)’ 矩阵V(:,1:4) % 不等于 I= 1.0000 0.0000 0.0508 -0.2348 0.0000 1.0000 -0.1256 0.2801 0.0508 -0.1256 1.0000 -0.0000 -0.2348 0.2801 -0.0000 1.0000>> U(:,1:4)’ 矩阵A*U(:,1:4) % 不等于 T= 1.7766 0.9747 -0.0322 -0.1440

如果计算 $T(2:4,2:4)$ 和 $T(3:4,3:4)$ 的特征值，我们会发现它们具有共同的特征值 $\lambda=4.7815,2.5089$。这种情况仅当 $T(3,2)=0$ 时才会发生。可通过使用三对角矩阵的递推公式验证，见第 6.7.1 节。这些公共特征值是由 $U(:,3: 4)$ 引入的，应予以舍弃。

eigSymByQR_(T(1:4,1:4),100 eps ,’short’)’= 1.0000 3.0000 4.7815 2.5089>> eigSymByQR_(T(2:4,2:4),100 eps ,’short’)’= 2.2234 4.7815 2.5089>> eigSymByQR_(T(3:4,3:4),100*eps ,’short’)’= 4.7815 2.5089

**选择性重新正交化** 参见 [61]。我们将前两个 Lanczos 递推公式重写如下，并包含浮点误差：
$$
T_{21}U(:,2)= AU(:,1)- T_{11}U(:,1)+ \epsilon_2, T_{32}U(:,3)= AU(:,2)- T_{21}U(:,1)- T_{22}U(:,2)+ \epsilon_3.
$$
现在我们计算 $T_{32}U(:,1)'U(:,3) -T_{21}U(:,2)'U(:,2)$，考虑到 $U(:,1)'A U(:,2) =U(:,2)'A U(:,1)$，$U(:,1)'U(:,1) =U(:,2)'U(:,2) = 1$，以及 $U(:,1)'U(:,2) =U(:,2)'U(:,1) = \epsilon$，由于矩阵 $A$ 的对称性以及显式归一化和正交化，
$$
T_{32}U(:,1)'U(:,3)=(T_{11} - T_{22}) \epsilon+ U(:,1)'\epsilon_3 - U(:,2)'\epsilon_2.
$$
最后两项的顺序为 $\epsilon \|矩阵A\|$。对于 $\|矩阵A\|$ 的估计，$U(:,1)'U(:,3)$ 可按如下方式估计：
$$
\|U(:,1)'U(:,3)\| = \epsilon\frac{\|T_{11} - T_{22}\| + \|A\|}{T_{32}}. \tag{7.12}
$$
以同样的方式，对于 $j = 1, ..., m$，有 $U(:,j - 1)'U(:,j) = \epsilon, U(:,j)'U(:,j) = 1$，而 $\|U(:,i)'U(:,j)\|, i=1, ..., j - 1$ 可通过类似于方程 $(7.12)$ 的递推公式进行估计。

当任意 $\|U(:,i)'U(:,j)\|,i= 1,..., j - 1$ 达到阈值时，对 $U(:,i)$ 到 $U(:,j)$ 进行显式重新正交化。然后将 $\|U(:,i)'U(:,j)\|$ 设为 $\epsilon$，并继续 Lanczos 递推。设置阈值为 $\sqrt{\epsilon}$ 即可保证所计算的 $T$ 是矩阵 $A$ 在由 $U$ 张成空间的子空间上的完全精确投影，
$$
T(1: j,1: j)= N'AN+ E, \|E\|= O(\epsilon \|A\|).
$$
这里，$N$ 是 $U(:,1 : j)$ 所张成子空间的正交基。尽管 $N$ 并未显式给出，但我们知道 $T(1 : j, 1 : j)$ 的特征值完全近似了矩阵 $A$ 在由 $U(:,1 : j)$ 张成的限制子空间上的特征值。

### 7.3.3 隐式重启对于更好的近似不变子空间

在满足 $U(:,1 : m)$ 的正交性条件下，$T(1 : m,1 : m)$ 是否能够逼近矩阵 $A$ 的期望的特征值，完全取决于 $U(:,1 : m)$ 是否包含了矩阵 $A$ 的期望的不变子空间。如果初始向量 $q$ 属于矩阵 $A$ 的期望的不变子空间，则 $T(m+ 1, m)= 0$ 对于某些
$m< n$，我们得到一个不变子空间。增加 $m$ 将增加 $\text{span}(U(:,1 : m))$ 的丰富性，从而提高其包含期望的不变子空间的可能性。在极端情况下，取 $m= n$ 可得到 $R^n$ 的整个空间，但这完全是不必要的。我们的目标是使用 $m \ll n$。策略是基于矩阵 $T(1 : m, 1 : m)$ 特征值解所提供的信息，用一个更优的 $q$ 重启基本 Lanczos 算法。隐式重启是一种更优的策略，它不仅提供更优的 $q$，还能节省 Lanczos 三项递推中的递归步骤。

我们假设重启时的新 $q$，记为 $q^+$，是从兰索斯向量 $Q(:,1 : m)$ 的张成空间中选取的，
$$
q^+= Q(:,1: m)p= p(A) q= Vp(\Lambda)V'q, \tag{7.13}
$$
对于某个数组 $p \in R^m$ 或某个次数为 $m - 1$ 的多项式 $p$，其中 $\Lambda$ 和 $V$ 是矩阵 $A$ 的特征值和特征向量。假设该多项式具有以下形式，其中下标表示多项式的次数，
$$
p_m(\lambda)=(\lambda - \theta_1)(\lambda - \theta_2) \cdots(\lambda - \theta_k)p_l(\lambda)= p_k(\lambda)p_l(\lambda), m= k+ l. \tag{7.14}
$$
如果 $\theta_j，j= 1，...，k$ 是不希望的特征值，则 $p( \lambda)$ 在这些位置附近取值较小，且 $q^+$ 在对应的特征向量上的分量也较小。因此，选择一个更好的 $q$ 就相当于选择一个多项式 $p$，使其强调期望的不变子空间的分量，同时弱化不期望的不变子空间的分量。

给定一组特征值 $\lambda_j，j= 1，...，m$，应由程序用户决定哪些是不需要的。用户可以决定编写一个函数，根据某些规范来选择特定的 $\lambda_j$。该函数应如下所示。

函数 pick =user_pick_(spec,neig,lambda ,lambdaj)
选择 = 0；如果 (lambdaj 属于满足 spec 和 neig 的 lambda) 选择 = 1；结束

从 $m$ 个特征值中选择 $k$ 个特征值的以下示例可能对许多用户具有实际意义。
1. 最大模（'LM'）或最小模（'SM'）。2. 最大实部（'LR'）或最小实部（'SR'）。
3. 最大绝对实部（'LRM'）或最小绝对实部（'SRM'）。4. 最大虚部（'LI'）或最小虚部（'SI'）。5. 最大绝对虚部（'LIM'）或最小绝对虚部（'SIM'）。

以下列出了基于这些选择规范的选择代码。

**算法 7.2**
根据 `spec` 从 `v` 中选择 `vj= ’LM’,’SM’,...,’SIM’` % 根据 `spec` 对 `v` 进行排序。如果 (`vj - >[v (1) ,v ( k )]`) 选择 =1；否则选择 =0。函数 pick = pick_(spec ,k,v,vj)[m,n]= size(v); spec = upper(spec); 如果 (n == 2) % 复共轭 [vr , vi ; - vi , vr ]==> [vr , vi ; vr , vi ]如果 (vj(1,2) ~= 0) vj(2,1) = vj(1,1); vj(2,2)=vj(1,2); 结束

j= 1; while(j< m) if(v(j,2)~= 0) v(j+1,1)= v(j,1); v(j+1,2)= v(j,2); j= j+ 1; end j= j+ 1; end end 如果 (strcmp(spec ,’LM’) || strcmp(spec ,’SM’)) % 最大（最小）模 u= zeros(m,1); 对于 j=1:m u(j)= 范数(v(j,:)); 结束 否则如果 (strcmp(spec ,’LR’) || strcmp(spec ,’SR’)) % 最大（最小）实部 u= v(:,1); 否则如果 (strcmp(spec ,’LRM’) || strcmp(spec ,’SRM’)) % 最大（最小）实部 |实部|u= abs(v(:,1)); 否则如果 (n==2&&(strcmp(spec ,’LI’) || strcmp(spec ,’SI’))) % 最大（最小）虚部 u= v(:,2); 否则如果 (n==2&&(strcmp(spec ,’LIM’) || strcmp(spec ,’SIM’))) % 最大（最小）虚部 |虚部|u= abs(v(:,2)); 否则 误差(‘pick_: ␣无效的第三个参数。’); 结束
如果 (spec(1) == ’L’)[u,p]= sort(u,’descend’); 否则 [u,p]= sort(u,’ascend’); 结束 v= permute_(p,v,’row’); j = 1; 选择 = 0;
while (j<=k) 如果 (n==1&& vj(1,1)==v(j,1) ||… n==2&& vj(1,1)== v(j,1) && vj(1,2)==v(j,2)) 选择 = 1; 跳出; 结束 如果 (n==