单源最短路径
对于图G =(V,E),给定源点 s 属于 V ,单源路径是指从 s 到图中其他各顶点的最短路径.
下图为带权有向图,从 v0 到其余各个顶点的最短路径如表所示。
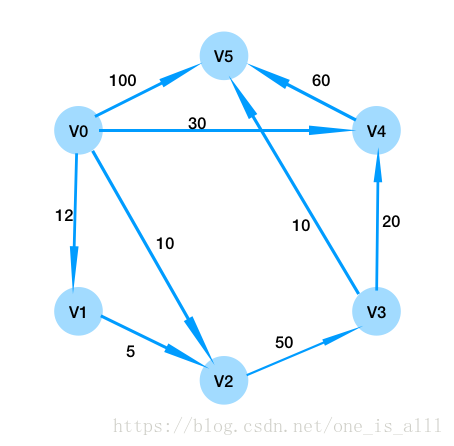
| 源点 | 终点 | 最短路径 | 路径长度 |
|---|---|---|---|
| v0 | v1 | V0->v1 | 12 |
| v2 | v0->v2 | 10 | |
| v3 | v0->v4->v3 | 50 | |
| v4 | v0->v4 | 30 | |
 本文介绍了Dijkstra算法用于求解单源最短路径问题,详细解释了算法的原理,并提供了C++代码实现。在带权有向图中,Dijkstra算法通过不断更新最短路径集合S和未确定路径集合V-S来找到从源点到所有顶点的最短路径。
本文介绍了Dijkstra算法用于求解单源最短路径问题,详细解释了算法的原理,并提供了C++代码实现。在带权有向图中,Dijkstra算法通过不断更新最短路径集合S和未确定路径集合V-S来找到从源点到所有顶点的最短路径。
对于图G =(V,E),给定源点 s 属于 V ,单源路径是指从 s 到图中其他各顶点的最短路径.
下图为带权有向图,从 v0 到其余各个顶点的最短路径如表所示。

| 源点 | 终点 | 最短路径 | 路径长度 |
|---|---|---|---|
| v0 | v1 | V0->v1 | 12 |
| v2 | v0->v2 | 10 | |
| v3 | v0->v4->v3 | 50 | |
| v4 | v0->v4 | 30 | |
 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


