文章内容部分源自北邮鲁鹏老师课上内容,侵删。
前言
之前学到损失函数的计算,以多类支持向量机损失为例。
一、简单回顾损失函数
损失函数公式:
L
=
1
N
∑
i
L
i
(
f
(
x
i
,
W
)
,
y
i
)
L=\frac{1}{N} \sum_{i}L_i(f(x_i,W),y_i)
L=N1∑iLi(f(xi,W),yi)
单样本的多类支持向量机损失:
L
i
=
∑
j
≠
y
i
m
a
x
(
0
,
s
i
j
−
s
y
i
+
1
)
L_i=\sum_{j\neq y_i}max(0,s_{ij}-s_{yi}+1)
Li=∑j=yimax(0,sij−syi+1)
线性分类器:
s
i
j
=
w
j
T
x
i
+
b
j
s_{ij}=w_j^Tx_i+b_j
sij=wjTxi+bj
问题一:多类支持向量机损失
L
i
L_i
Li的最大、最小值?
答:最大:无穷大,观察线性分类器的表达式,
s
i
j
s_{ij}
sij的值是不确定的可能是无穷大。
问题二:如果初始化w和b都很小,损失L是多少。
答:观察单样本多类支持向量机损失公式,假设w,b都是0,则
L
i
L_i
Li为类别数-1。
注意:可以使用这一点来判断自己编码是否正确,若设置w,b都为0,则输出的
L
i
L_i
Li一定是类别数-1
问题三:考虑所有类别(包括
j
=
y
i
j=y_i
j=yi),损失
L
i
L_i
Li会有什么变化?
答:+1
问题四:在计算总损失L时,如果用求和代替平均?
答:没有影响。
问题五:如果使用
L
i
=
∑
j
≠
y
i
m
a
x
(
0
,
s
j
−
s
y
i
+
1
)
2
L_i=\sum_{j\neq y_i}max(0,s_j-s_{yi}+1)^2
Li=∑j=yimax(0,sj−syi+1)2
答:影响可能很大,因为假设有一个值时100,平方就成了10000,另一个值是0.01,就成了0.0001,区别会很大。
二、正则项与超参数
1.问题引入
假设:存在一个W使损失函数L=0,这个W是唯一的吗?

如上图所示,存在了两个分类器,使得对于通过一张照片的损失都为0。
那如何选择w1与w2呢?
2.引入正则项

超参数:
· 在开始学习之前设置的参数,不是学习得到的。
· 超参数一般都会对模型性能有重要影响。
上式中,假设
λ
\lambda
λ = 0 那么优化结果仅与数据损失有关,表现越好,优化效果越好。
假设
λ
=
∞
\lambda=\infty
λ=∞ 优化结果与数据损失无关,仅考虑权重损失,此时系统最优解为W=0。

L2损失示例
样本:x=[1,1,1,1]
分类器1: w 1 = [ 1 , 0 , 0 , 0 ] w_1=[1,0,0,0] w1=[1,0,0,0]
分类器2: w 1 = [ 0.25 , 0.25 , 0.25 , 0.25 ] w_1=[0.25,0.25,0.25,0.25] w1=[0.25,0.25,0.25,0.25]
分类器输出: W 1 T x = W 2 T x = 1 W^T_1x=W^T_2x=1 W1Tx=W2Tx=1,二者的数据损失是一样的。
假设 λ = 1 \lambda = 1 λ=1,正则损失: R ( w 1 ) = 1 R ( w 2 ) = 0.25 R(w_1)=1 R(w_2) = 0.25 R(w1)=1R(w2)=0.25
所以 w 2 w_2 w2总损失小
L2正则损失对大数值权值进行惩罚,喜欢分散权值,鼓励分类器将所有维度的特征都用起来,而不是强烈的依赖其中少数几维特征。也可以预防过拟合。
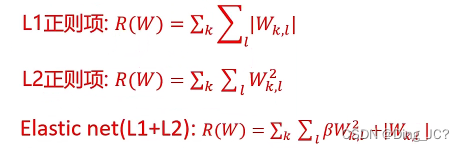
优化
什么是参数优化
参数优化是机器学习的核心步骤之一,它利用损失函数的输出值作为反馈信身来调整分类器参数,以提升分类器对训练样本的预测性能)
优化算法目标
损失函数L是一个与参数W有关的函数,优化的目标就是找到使损失函数L达到最优的那组参数W。
直接方法
∂
L
∂
W
=
0
\frac{\partial L}{ \partial W} =0
∂W∂L=0
梯度下降算法
再更新
总结
提示:这里对文章进行总结:
例如:以上就是今天要讲的内容,本文仅仅简单介绍了pandas的使用,而pandas提供了大量能使我们快速便捷地处理数据的函数和方法。







 本文介绍了多类支持向量机损失函数及其性质,重点讨论了引入正则项(如L2范数)的必要性,解释了如何通过超参数调节防止过拟合,以及如何通过梯度下降优化算法在损失函数中寻找最优解。通过实例展示了L2正则如何影响模型选择和性能。
本文介绍了多类支持向量机损失函数及其性质,重点讨论了引入正则项(如L2范数)的必要性,解释了如何通过超参数调节防止过拟合,以及如何通过梯度下降优化算法在损失函数中寻找最优解。通过实例展示了L2正则如何影响模型选择和性能。
















 779
779

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








