本文深入解析了选择排序、插入排序、冒泡排序、希尔排序、归并排序和快速排序的算法原理及实现。通过详细的代码示例，展示了每种排序算法的特点和适用场景。
自己愚笨，简单的排算法，都要理解很久。不过也好歹算是自以为是地理解了一点，用自己的语言，将算法的过程和思想进行描述。可能会比较啰嗦，但好在此篇博文不为悦人，只为悦己。但如果万一能对人有帮助的话，那就更好了。
如果有疏漏和理解错误的地方，还请不吝批评指正，谢谢！
选择排序
package sort;
import java.util.Arrays;
/**
* 选择排序
* 就是每次先找到没有排序中的最小的值的下标，然后呢，将最小下标的值与当前没有排序的最左边的数进行交换。
* 外围循环的i，主要控制目前左边已经有多少个已经排好序了，j就不要再向左了，一直到不能更右的时候，
* 就排好序了。
* @author owon
*
*/
public class SelectSort {
public static int[] selectSort(int[] a) {
int temp = 0;
System.out.println("初始数组："+Arrays.toString(a));
for(int i = 0; i < a.length-1; i++) {
int minIndex = i;
for(int j = i+1; j < a.length;j++) {
if(a[minIndex]>a[j] ) {
minIndex = j;
}
}
temp = a[minIndex];
a[minIndex] = a[i];
a[i] = temp;
int k = i +1;
System.out.println("第"+k+"次："+Arrays.toString(a));
}
return a;
}
public static void main(String[] args) {
int[] a = {5,6,8,2,9,3,7,4};
selectSort(a);
//System.out.println(Arrays.toString(a));
}
}
插入排序
package sort;
import java.util.Arrays;
/**
* 插入排序
* 没有那么复杂，只是将每次外部循环的起点作为一个哨兵，左边的，都是排好序的，右边的都是无序的数组；
* 那么每次外部确定的那个，都是要必须进行排序的，必须放在一个有序的位置；
* 而这个位置是在有序的数组中找到的，所有放进去，在整体上看，像是插进去的一样，故名插入排序。
* 但实现方式上，还是一般的交换得来的。
* @author owon
*
*/
public class InsertSort {
public static int[] insertSort(int[] arr) {
int temp;
for(int i = 1;i<arr.length;i++) {
for(int j = i;j > 0;j--) {
if(arr[j ]<arr[j-1]) {
temp = arr[j];
arr[j ]=arr[j-1];
arr[j-1] = temp;
}
}
System.out.println(Arrays.toString(arr));
}
return arr;
}
public static void main(String[] args) {
int[] arr = {5,6,8,2,9,3,7,4};
insertSort(arr);
System.out.println(Arrays.toString(arr));
}
}
冒泡排序
package sort;
import java.util.Arrays;
/**
* 冒泡排序，这里的i，主要作用是，控制j到哪里停止。
* 外面每循环一次，就有一个最大值已经放到最右边了。
* 那么，循环i次的话，就有i的最大值已经排好了，此时，内部循环就不在需要再进入到已经排好序的右边了。
* 这个排序，跟选择排序有些相似之处。
* 选择排序是把左边小的都排好，然后j就不要往左边去了。
* 冒泡排序是右边大的都排好，j就不要再往右边晃悠了。
* @author owon
*
*/
public class BubbleSort {
public static int[] bubbleSort(int[] arr) {
int temp;
//i控制j到哪里停止，具体来说，就是目前已经有多少个排好序的，初始是0个
//然后外循环一次，找到了最大值，放到最右边，然后呢，你j的最大下标呢，就减i吧。
//因此，j内循环是与要从最初始的，一点一点地减去外循环的次数（排好序的个数）。
for(int i=0;i<arr.length-1;i++) {
for(int j=1;j<arr.length-i;j++) {
if(arr[j] < arr[j-1]) {
temp = arr[j-1];
arr[j-1 ] = arr[j];
arr[j] = temp;
}
}
System.out.println(Arrays.toString(arr));
}
return arr;
}
public static void main(String[] args) {
int[] arr = {5,6,8,2,9,3,7,4};
bubbleSort(arr);
System.out.println(Arrays.toString(arr));
}
}
希尔排序
package sort;
import java.util.Arrays;
/**
* 希尔排序
* 是由大到小的一种思想，由不同步长之下，不同分组之下，遍历每个分组，进行排序。
* 所以需要三重循环，至少看起来是这样的三重循环。
* @author owon
*
*/
public class ShellSort {
public static int[] shellSort(int[] arr) {
int n = arr.length;
//控制步长，间距
for(int h = n/2;h>0;h = h/2 ) {
//对各个局部分组进行插入排序
for(int i = h;i<n;i++) {
//此时在i之前，或者说是在h之前，所有的数都是自己组内的第一个数，所以不存在排序问题。
//此时，可以认为第一个这些数是有序的。所以对于i= h 的处理，也是基于这种考虑。
//从间距处开始，即此时的值对应数组第一个元素的值，它们是一个组的，所以此时，可以将这两个数排序。
//间距的第二个数，对应数组的第二个数，它们是一个组的，所以此时，是两个数排序，以此类推。
//当一直加到第三个间距时，则有第三个数插入到前面已经排序好的一个个数组中。
//所以，个人感觉，希尔排序就是一组一组的插入排序。
insertI(arr,h,i);
}
}
return arr;
}
/*
* 由给定的间距，和起始点，然后对数组进行遍历循环，进行排序。
* 这个就是一个一个的插入排序了，一个要进行排序的数组，确定了它的步长和起始位置，那么就可以确定了这个子数组的元素。
* 此时，由定位的元素，向前找到与它相差步长的数，进行插入排序。
* 此函数控制的就是这个过程。
* 而它之外的两个循环，一个呢，是确定步长，从总数组的 1/2 ，每间隔这么远取值。直到间隔为1。
* 另一个循环呢，是确定起始的位置。从arr[步长]开始，到结束。然后每个起始位置都会再进行循环。
* 最后一个循环呢，就是插入排序的循环。从上一步的内一个起始位置，由后向前，每隔最外围步长，为一组
* 取出来，进行比较。
* 又因为插入排序，是前面已经排序好了。不过这种排序好了，它是相对的。我只是在一个无序的数组中，从前向后，一个一个地排好序。
* 只管前面的，后面的没有遍历到，不管。
* 所以每次遍历到后面的那一个，都要在前面的排好序中的数组，找到自己的位置。从后向前，一个一个地比较。
* 我比你小，好，咱俩交换，我向前一步。我比你又小，再向前。直到找到一个位置，比前面的大，比后面的小
* 那么就排序好了。
* 然后，再向后一个位置遍历，直到最后一个元素插入到前面适合它的位置，那么就排序完成了。
*/
public static void insertI(int[] arr, int h, int i) {
int temp = arr[i];
for(int j = i;j>0 && j-h>=0;j=j-h) {
if(arr[j] < arr[j-h]) {
temp = arr[j];
arr[j] = arr[j-h];
arr[j-h] = temp;
}
}
}
public static void main(String[] args) {
int[] a = {5,6,8,2,9,3,7,4};
shellSort(a);
System.out.println(Arrays.toString(a));
}
}
归并排序
我还画了过程的逻辑图，先贴上去，便于理解，如果有问题，还请不吝指出！
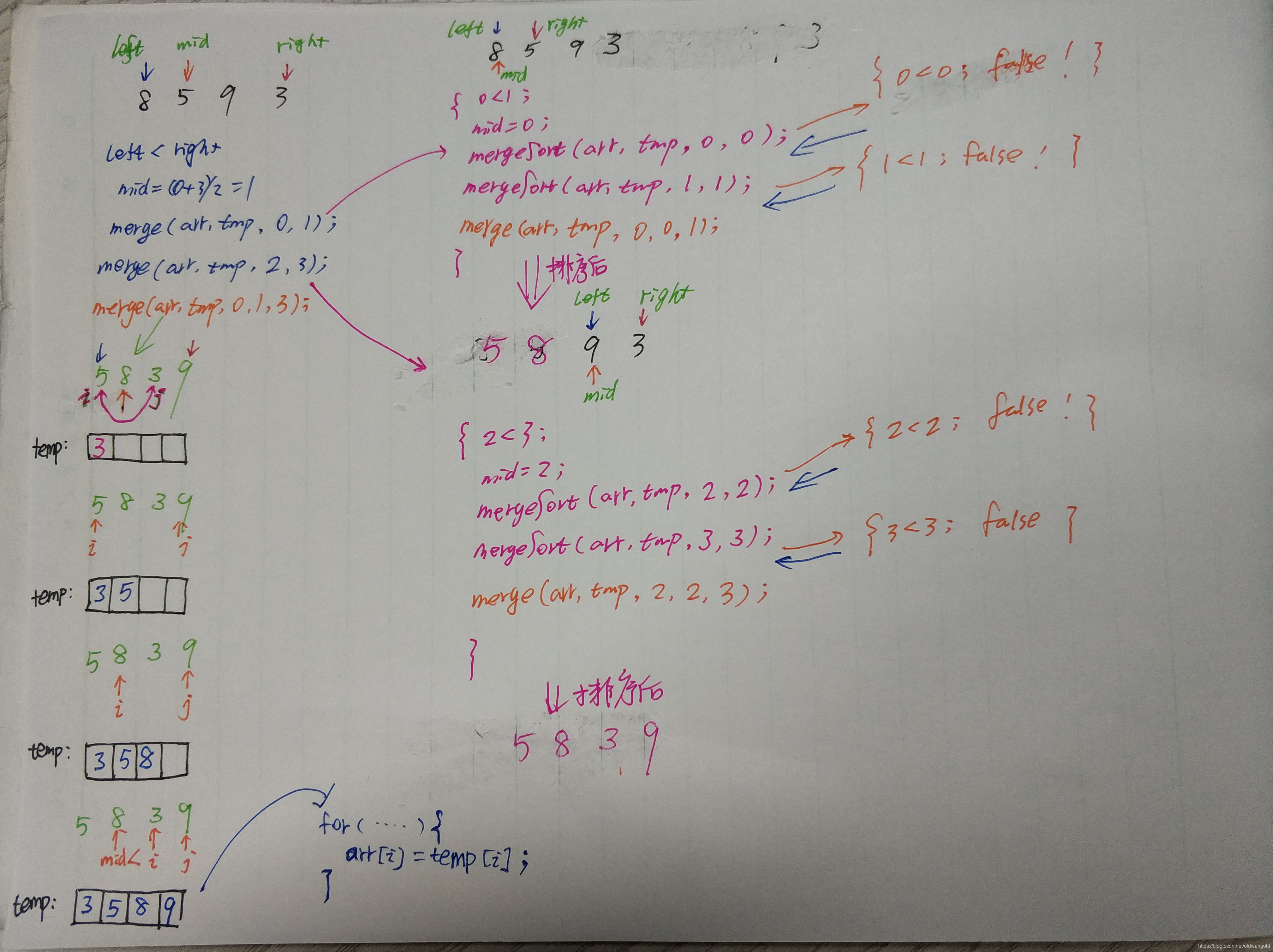
import java.util.Arrays;
/**
* 归并排序 将数组arr[left] ---> arr[right] 进行归并排序
* @param arr 要排序的数组
* @param temp 辅助数组
* @param left 左边界
* @param right 右边界
* @author owon
*归并排序的核心思想是分治，分而治之。将一个大问题分解长无数的小问题进行处理，处理之后再合并，这里是采用递归实现的。
*关于第一步分的做法，主要还是进行指针的移动，分别将指针移动到当次递归所需的left、right、mid中，分到不能再分的时候，将此时数组部分的指针传递到治的函数，进行治的处理。
*需要注意的是，整个分治过程，数组还是这个数组，我们处理的也还是同一个它，如果有什么区别的话，那要么就是我们每次处理的范围不同罢了，看的局部不同罢了。
*有些动图和讲解，会 拿那些片段进行讲解，不过不要被迷惑，他们只是拿着片段给咱们看，好把问题讲清楚。但整个处理过程，没有新增任何一个数组，只有我们的辅助数组和要排序的数组，没有其他！
*
*/
public class MergeSort {
public static void mergeSort(int[] arr,int[] temp,int left,int right) {
if(left<right) {
//中点坐标
int mid = (left+right)/2;
//分
mergeSort(arr,temp,left,mid);
mergeSort(arr,temp,mid+1,right);
//归并
merge(arr,temp,left,mid,right);
}
}
private static void merge(int[] arr, int[] temp, int left,int mid, int right) {
int i = left,j = mid + 1;
//k是temp数组的下标值，保证每次存入temp数组的元素是在当时排序范围内的相应范围。
//也可说，每次操作的待排序的部分，在辅助数组相对应的下标处。
//应该是这样的
//O O O O O O O O 辅助数组
// 1 1 1 1 归并的部分
//2 2 2 2 归并的另一部分
//x x x x x x x x 整个数组进行归并
//即，在区域内进行归并时，使用相应区域的数组，全使用时，用整个数组。
for(int k = left;k <= right;k++) {
if(i > mid) {
temp[k] = arr[j];
j++;
}else if(j > right) {
temp[k] = arr[i];
i++;
}else if(arr[i] <= arr[j]) {
temp[k] = arr[i];
i++;
}else {
temp[k] = arr[j];
j++;
}
}
//千万不可忘记最后还得将排好序的数组，赋值给原数组，这样最后才是原数组排好了序的。
for(int k = left;k<=right;k++) {
arr[k] = temp[k];
}
}
public static void main(String[] args) {
int[] a = {5,6,8,2,9,3,7,4};
int[] temp = new int[a.length];
mergeSort(a,temp,0,a.length-1);
System.out.println(Arrays.toString(a));
}
}
又参考了下别人的实现，觉得自己的应该再改进一点，应该可以实现传入要排序的数组就可以实现排序，封装一下，不然看起来有点chun。
public static void mergeSort(int[] arr) {
int[] temp = new int[arr.length];
mergeSort(arr,temp,0,arr.length-1);
}
这个时候，对一个数组进行归并排序，只需要mergeSort(arr)一下，就可以了，如果想要对一定范围进行排序，再指定好了。
还有，上面是递方式，万一面试官让写个非递归的，肿么办？那就借鉴写别人写好的吧。。。
//非递归的实现方式
public static int[] mergeSort(int[] arr) {
int n = arr.length;
// 子数组的大小分别为1，2，4，8...
// 刚开始合并的数组大小是1，接着是2，接着4....
for (int i = 1; i < n; i += i) {
//进行数组进行划分
int left = 0;
int mid = left + i - 1;
int right = mid + i;
//进行合并，对数组大小为 i 的数组进行两两合并
while (right < n) {
// 合并函数和递归式的合并函数一样
merge(arr, left, mid, right);
left = right + 1;
mid = left + i - 1;
right = mid + i;
}
// 还有一些被遗漏的数组没合并，千万别忘了
// 因为不可能每个字数组的大小都刚好为 i
if (left < n && mid < n) {
merge(arr, left, mid, n - 1);
}
}
return arr;
}
// 合并函数，把两个有序的数组合并起来
// arr[left..mif]表示一个数组，arr[mid+1 .. right]表示一个数组
private static void merge(int[] arr, int left, int mid, int right) {
//先用一个临时数组把他们合并汇总起来
int[] a = new int[right - left + 1];
int i = left;
int j = mid + 1;
int k = 0;
while (i <= mid && j <= right) {
if (arr[i] < arr[j]) {
a[k++] = arr[i++];
} else {
a[k++] = arr[j++];
}
}
while(i <= mid) a[k++] = arr[i++];
while(j <= right) a[k++] = arr[j++];
// 把临时数组复制到原数组
for (i = 0; i < k; i++) {
arr[left++] = a[i];
}
}
public static void main(String[] args) {
int[] a = {5,6,8,2,9,3,7,4};
int[] temp = new int[a.length];
mergeSort(a);
System.out.println(Arrays.toString(a));
}
非递归的算法几乎也差不多，就是顺着一点一点来，先从最小的子数组进行排序，相邻两两排好序，然后再四个、八个排好序，直到总的都排队序。如果说递归是自顶向下，那么非递归就有点像是自底向上。不过最后的结果都一样的。
快速排序
快排的核心思想也是分治法，分而治之。具体就是每次选一个基准值，其他值依次比较，实现比基准值大的放右边，比基准值小的放左边。然后再对左右两边除了自己，再选基准值，依次递归实现。按照我个人的理解，就是将一堆萝卜分堆。先找一大堆萝卜中的一个为参考，左边的都不比它大，右边都比它大。好的，那这个就放在这两堆中间，不用动了。
然后对左边这一堆也是，随便选一个，比它大的放右边，其他的放左边；同时右边的这一堆也一样。
那么此时，我有了四堆萝卜，三个已经能确定的萝卜。
大概可以这样：
一堆萝卜
( 左半堆) <= 萝卜1 < (右半堆)
(左左半堆 <= 萝卜2 < 左右半堆) <= 萝卜1 < (右左半堆 <= 萝卜3 < 右右半堆)
这样就很清晰了，继续递归下去，可以推得，所有的萝卜都会按序排好。
import java.util.Arrays;
public class QuickSort {
public static void quickSort(int[] arr) {
quickSort(arr,0,arr.length-1);
}
public static void quickSort(int[] arr,int startIndex,int endIndex) {
if(endIndex <= startIndex) {
return ;
}
//切分,找到最佳的切分点，在这个切分点，左边的所有元素都是小于这个切分点的，右边所有的元素都是大于切分点的。
//然后再进行递归排序，找到子递归序列的最佳切分点，对左边和右边进行切分。
int pivotIndex = partition(arr,startIndex,endIndex);
//非常需要注意的一点是，再进行递归快速排序的时候，使已经将切分点去除的，所以如果第一次是一共有n个元素进行选点的话。
//选到的这个元素，其实就在了自己最终的位置，然后在左子序列中进行选点，此时共有(n-1)/2个元素，然后再是((n-1)/2-1)/2
//一直到不可划分一个元素自成一派。
//这就像是，n个萝卜放n个坑，但是并不是每一个萝卜跟自己的坑都是对的，所以我们就每次进行切分
//找到一个萝卜，放到自己的坑里。然后再将这个萝卜忽略，在其他的萝卜群里再找坑，找到合适的就忽略。
//最后将所有的萝卜都放到属于自己的坑里面。
quickSort(arr,startIndex,pivotIndex-1);
quickSort(arr,pivotIndex+1,endIndex);
}
private static int partition(int[] arr, int startIndex, int endIndex) {
int left = startIndex;
int right = endIndex;
//取第一个元素为基准值
int pivot = arr[startIndex];
while(true) {
//从左向右扫描，如果自己的值不大于中轴元素，不停止，直到左右坐标相等了或者大于了
while(arr[left] <= pivot) {
left++;
if(left > right) {
break;
}
}
//从右向左扫描
while(arr[right] > pivot) {
right--;
if(right < left) {
break;
}
}
//左右指针相遇，那么就证明刚好是这个位置
if(left > right) {
break;
}
//交换左右的数据，是的左边的元素不大于pivot，右边的大于pivot
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
}
//将基准值插入到序列中
int temp = arr[startIndex];
arr[startIndex] = arr[right];
arr[right] = temp;
return right;
}
public static void main(String[] args) {
int[] a = {5,6,8,2,9,3,7,4};
int[] temp = new int[a.length];
quickSort(a);
System.out.println(Arrays.toString(a));
}
}
并且需要注意的是，对于一篇文章的参考，他对于扫描的边界指针值的判断是有问题的，我将代码进行测试，没得到正确值，最后分析时发现，他的判断扫描的退出条件是：
if (left == right) {
break;
}
其实是不行的，假设刚好我左半堆只有一个萝卜，那么我的left是等于right的，此时从左向右扫描，left已经大于right了，很显然只有当外层while循环条件不满足时，才会结束循环。但在这之间，经历了什么，我们不知道，但可以肯定的是，这样不对并且很危险。
不过经过我改了判断条件之后，输出了正确答案了。
扫一扫
2431
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
