位运算精讲与实战-优快云博客

位运算就是将一个数字用二进制的方式表示出来，对每一位上的0、1进行的运算。

位运算有五种：与、或，异或、左移、右移。

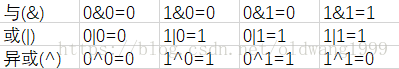
左移运算符：m<<n，表示把m左移n位。

例：00010101<<2=01010100

右移运算符：m>>n，表示把m右移n位。

例：00010101>>2=00000101

题目一

当我们看到题目，很快就形成一个思路：我们每次先判断一个数的二进制的最右边是不是1，判断完之后整体右移一位，继续判断。用最右边的数和1做&运算，结果如果是1，就表示带整数最右边的一位是，否则就是0；

代码:

int NumOfOne(int n)
{
	int count = 0;
	while (n)
	{
		if (n & 1)
			count++;
		n = n >> 1;
	}
	return count;
}

右移虽然和除以2在数学上是等价的，但是除法的效率要比运算符低得多。

其实上边的代码是不完全对的，如果给的参数是0x80000000，也就是32位的10000000 00000000 00000000 00000000，对它右移就是01000000 00000000 00000000 00000000，但是要保证这个数是个负数，在移位后最高位就会默认为1，就变成11000000 00000000 00000000 00000000，即0xC0000000;如果这样走下去，最终这个数字就变成0xFFFFFFFF，程序就会死循环。

为了避免这样的死循环，我们可以换一种思路，让原来的数字不右移，首先让n和1做&运算，让1左移变成00000000 00000000 00000000 00000010，在和n做&运算，这样的反复左移就可以判断出哪一位上有1。

修改代码：

int NumOfOne(int n)
{
	int count = 0;
	unsigned int flag = 1;

	while (flag)
	{
		if (n&flag)
			count++;
		flag = flag << 1;
	}
	return count;
}

这样的代码虽然对，然是如果32位都是1，那么它就要循环32次。

究极思路：

我们把一个整数减去1，再和原来的整数做&运算，会把原来的数的最右边的1变成0，那么一个整数中有多少个1就进行多少次这样的操作。

例：1100（12）减1变成1011，再和1100做&运算，得到1000，就是将1100中第二个1变成0。

代码：

int NumOfOne(int n)
{
	int count = 0;
	while (n)
	{
		++count;
		n = (n - 1)&n;
	}
	return count;
}

相关题目：

1.用一条语句判断个整数是不是二的倍数

思路：

一个整数如果是二的倍数。那么它的二进制中有且只有一个1，通过“究极思路”，它唯一的1也就变成0；

代码：

void  PowerOfTwo(int n)
{
	if (n==0)//指数函数都大于0
		printf("NO\n");
	else if (((n - 1)&n) == 0)
		printf("YES\n");
	else
		printf("NO\n");
}

2.输入两个整数m，n，计算需要改变m的二进制中多少位，才能变成n。

思路：

例：m：13(1101) n: 8(1000)

第一步：m^n=0101

第二部：求异或的数中1的个数

代码：

int MtoN(int m,int n)
{
	int count = 0;
	int a = 0;
	a = m^n;
	while (a)
	{
		++count;
		a = (a - 1)&a;
	}
	return count;
}

3.写一个函数，求两个整数的和，要求在函数体内不得使用加，减，乘，除四则运算符号。

思路：不用四则运算，还要完成加法，毫无疑问，我们要用到位运算。我们可以分成三步：1.各位相加不进位；2.做进位；3.前两步相加

我们举个例子：15+7

15的二进制1111 7的二进制111

第一步：相加不进位1111+0111=1000，很明显这就是异或运算。

第二部：做进位1111+0111的进位就是1110，第一位的1和0没有进位，剩下三个位的1和1都有进位，这相当于1111&0111左移1位。

因为进位不是0所以继续重复一二步，直到不产生进位为止。

第一步：1000^1110=0110

第二步：1000&1110左移一位=10000 (进位不为0)

第一步：0110^10000=10110

第二部：0110&10000为0；

第三步：10110+0=10110为22

代码实现：

int ADD(int n1, int n2)
{
	int sum, count;
	do
	{
		sum = n1^n2;
		count = (n1&n2) << 1;
		n1 = sum;
		n2 = count;
	}
	while (n2!=0);
	return n1;
}
int main()
{
	int ret = ADD(15,7);
	system("pause");
	return 0;
}