文章目录
CS224W: Machine Learning with Graphs
公式输入请参考: 在线Latex公式
这节内容貌似也很重要,是针对大规模图数据的优化。之前对这方面的了解只知道用GraphSAGE可以分Batch,貌似还有别的方法。
针对无法对GNN进行随机梯度下降的问题,搞出了GraphSAGE;
针对无法将大图直接进行full batch计算的问题,搞出了Cluster-GCN;
针对GCN模型本身进行了简化,去掉了非线性的计算,并进行了化简。
Scaling Up GNNs to Large Graphs
当前图应用的数据量
| 应用 | 数据集 | 数据量 | 常见任务 | |
|---|---|---|---|---|
| Recommender systems | Amazon YouTube | Users(绿圆): 100M~1B Products/Videos(红方):10M ~ 1B | Recommend items(link prediction) Classify users/items(node classification) |  |
| Social networks | Facebook | Users:300M~3B | Friend recommendation (link-level) User property prediction(node-level) |  |
| Academic graph | Microsoft Academic Graph | Papers:120M Authors:120M | Paper categorization(node classification) Author collaboration recommendation Paper citation recommendation(link prediction) |  |
| Knowledge Graphs | Wikidata Freebase | Entities:80M~90M | KG completion Reasoning |  |
特点
尺寸大:节点数从10M到10B;边数量从100M到100B。
常见任务:
节点级别:User/item/paper classification
边级别:Recommendation, completion
SGD for GNN?
对于传统的ML优化方法当然就是GD:
l
(
θ
)
=
1
N
∑
i
=
0
N
−
1
l
i
(
θ
)
\mathcal{l}(\theta)=\cfrac{1}{N}\sum_{i=0}^{N-1}l_i(\theta)
l(θ)=N1i=0∑N−1li(θ)
对于数据量较大的时候,要计算所有的点再进行梯度更新效率很低,因此常用随机梯度下降法,每次随机取
M
(
<
<
N
)
M(<<N)
M(<<N)个样本形成mini-batches,这个时候计算
M
M
M个样本的梯度
l
s
u
b
(
θ
)
l_{sub}(\theta)
lsub(θ)更新即可:
θ
←
θ
−
▽
l
s
u
b
(
θ
)
\theta\leftarrow\theta-\triangledown l_{sub}(\theta)
θ←θ−▽lsub(θ)
那用这个思路把SGD用在GNN上来解决GNN面临的大数据量的问题可以吗?
假设我们从图中随机取
M
(
<
<
N
)
M(<<N)
M(<<N)个独立的节点
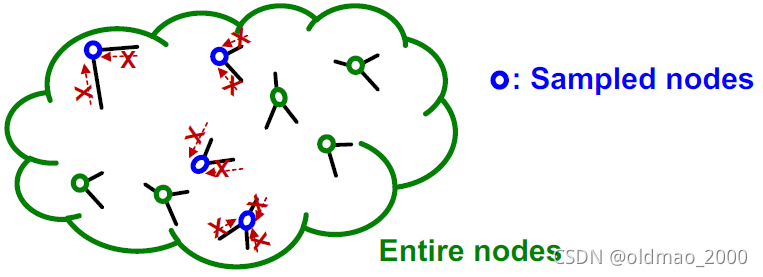
既然是独立的节点,那么采样出来的节点就是孤立的点,这样就没有办法做消息的聚合与传递了,GNN也没法玩了。
因此,原始的SGD无法用在GNN上。
Naïve full-batch implementation for GNN?
我们再看看Naïve full-batch的方式,每次生成所有节点的表征。
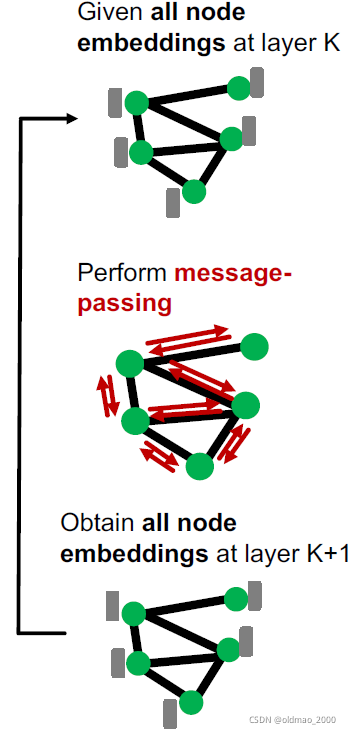
可以看到
1.训练过程需要加载全图的所有节点及特征
2.在每个GNN层中,都要基于前一层的所有节点的embedding计算当前层所有节点的embedding
3.计算损失
4.做GD
当前一般的DL都是用GPU来加速运算,GPU的内存一般是(10GB–20GB)6GB显存本本默默流泪。。。。这个数据量根本加载不进来:
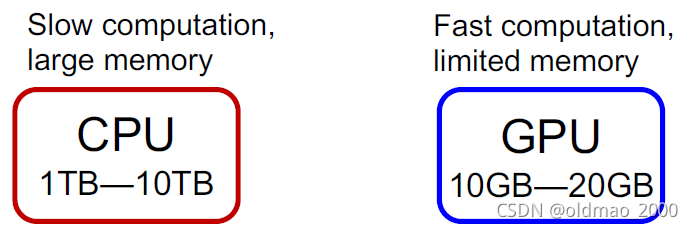
看了直接硬train也不行,下面看三种解决方案。
Neighbor Sampling: GraphSAGE1
之前写过2,这里看了讲解有新的领悟,重新整理一下。
这个方法改进有三个部分:
基于邻域的随机梯度下降
SGD之所以无法用在GNN上是因为单个节点的采样会丢失邻居的信息,导致GNN的消息汇聚然并卵。
从GNN的计算图中可以看到,一个K层GNN的消息汇聚只涉及到该节点的K跳邻居:
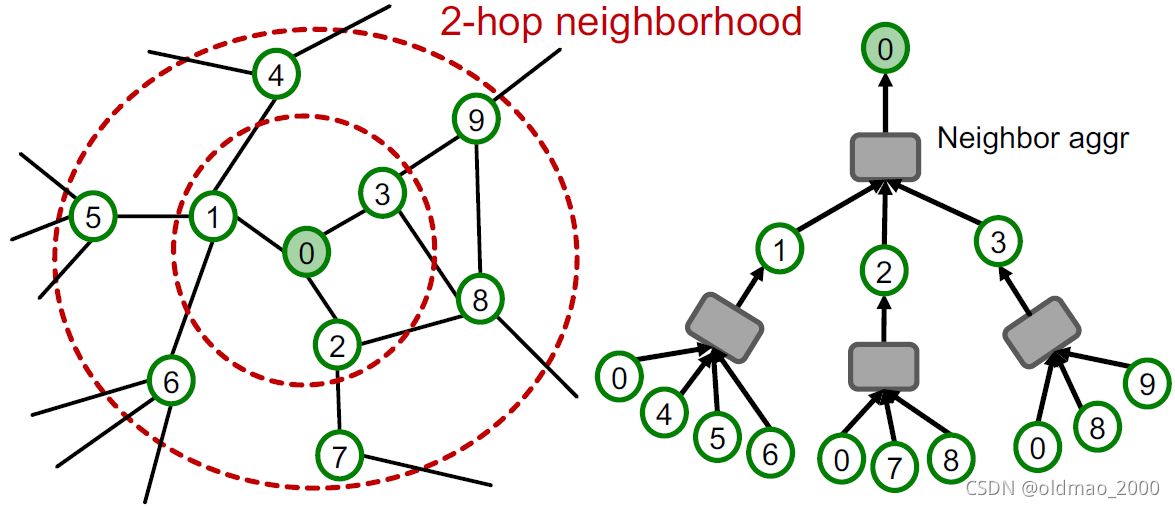
那么采样的时候不单单采样某个节点,而是直接将该节点以及其K跳邻域信息包含进来,形成mini-batch:
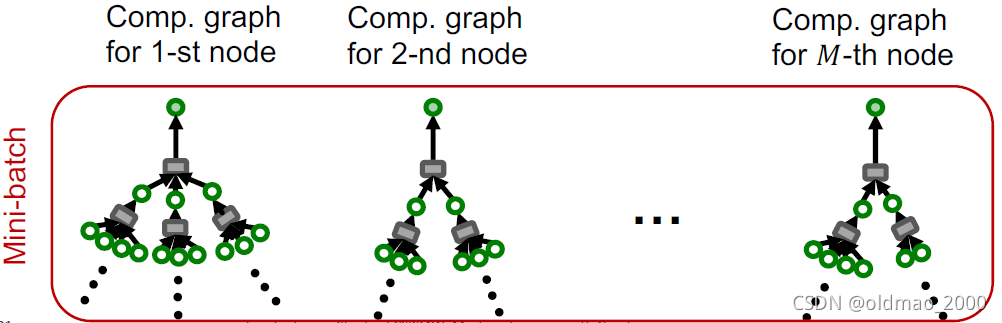
这样就得到了基于邻域的SGD算法,具体描述如下:
1.随机采样
M
(
<
<
N
)
M(<<N)
M(<<N)个节点
2.对于每个采样节点
v
v
v
2.1获取其K跳邻居,并构造计算图
2.2用计算图生成节点
v
v
v的embedding
3.计算
M
M
M个节点的梯度
l
s
u
b
(
θ
)
l_{sub}(\theta)
lsub(θ)
4.更新梯度:
θ
←
θ
−
▽
l
s
u
b
(
θ
)
\theta\leftarrow\theta-\triangledown l_{sub}(\theta)
θ←θ−▽lsub(θ)
好处与问题
这里将计算图代替单个节点,即可实现mini-batch,又能保证图的信息汇聚不变,当然是效率提高的,但是也存在一个问题。在2.1步中,生成计算图非常耗费资源,因为图的邻居节点数量增长是K跳的指数级:
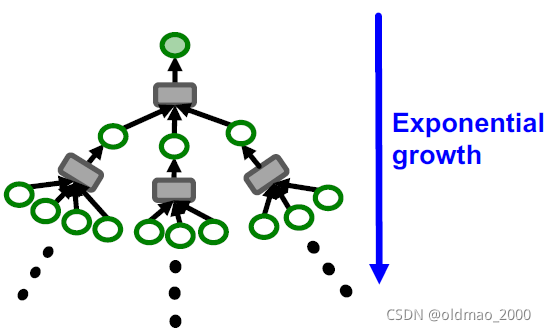
另外对于一些图中的超级节点,例如某个大V的粉丝好几百万,意味该节点的邻居超多,做2.2步的时候会很慢:
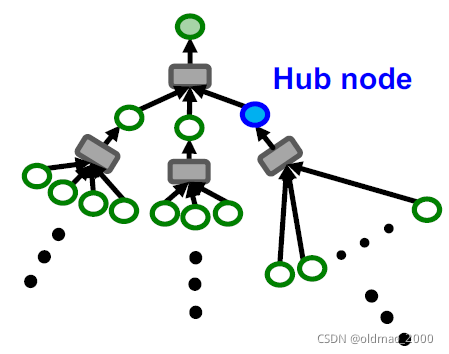
邻居采样
使用邻居采样进一步压缩计算图。这个也是SAGE的由来sample+aggregate。其思想就是在每跳邻居中采样
H
H
H个邻居,下面是
H
=
2
H=2
H=2的例子
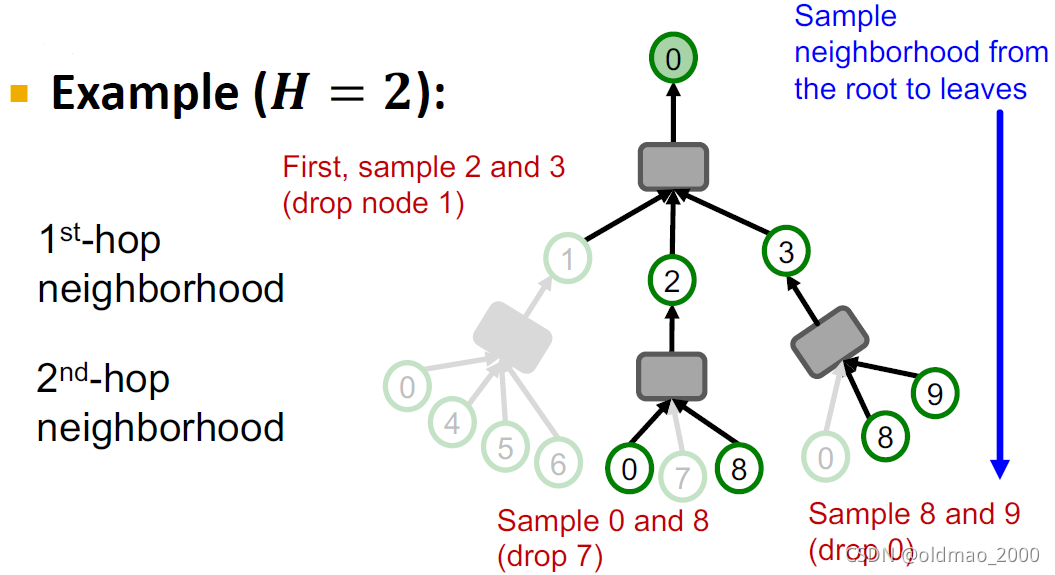
邻居采样(相当于计算树剪枝)后在进行SGD。这里只需要将前面的2.1换成下面的步骤:
对于K层GNN的邻居采样描述如下:
1.对于
k
=
1
,
2
,
⋯
,
K
:
k=1,2,\cdots,K:
k=1,2,⋯,K:
1.1对于每个第
k
k
k跳的邻居,最多随机采样
H
k
H_k
Hk个邻居
2.得到最多包含
∏
k
=
1
K
H
k
\prod_{k=1}^KH_k
∏k=1KHk个叶子节点的计算图
好处与问题
较小的
H
H
H可以使得邻居汇聚效率大大增加,但会使得模型的训练不够稳定,因为每次随机出来邻居不一样。
虽然有了
H
H
H个邻居的上限,计算图大小的上限仍然和K跳(GNN的层数也是它)呈指数关系,K增加还是会使得计算图变很大。
最大的问题是随机采样,因为图中的节点明显有不一样的重要程度,采样到不重要的邻居得到embedding的结果明显不是最优的。
邻居的选择
为了解决随机采样的问题,这块研究还有待进一步研究,目前的解决方法是采取策略来采样重要的点:
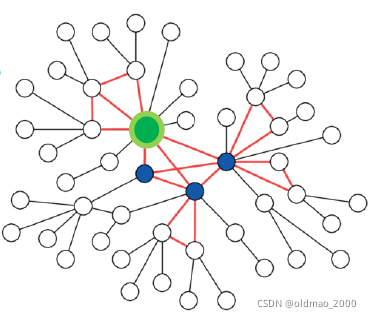
例如上图中的策略是:
从绿色点开始可回原地随机游走,并计算Restarts score:
R
i
R_i
Ri(直觉上:这个玩意越高说明该节点涉及到的内部节点越多,就是random walk with restarts,RWR算法)
在每层GNN的邻居采样中对高
R
i
R_i
Ri的邻居采样。
小结及改进思路
该方法是目前工业上应用较成熟的方法。pintrest?阿里都在用
但是该方法仍然有一些缺点:
1.计算图的大小仍然和GNN的层数成指数关系
2.计算过程非常冗余,尤其是当邻域中多个节点共享邻居的时候(在同一个mini-batch中),该邻居会在计算图中出现多次,例如:
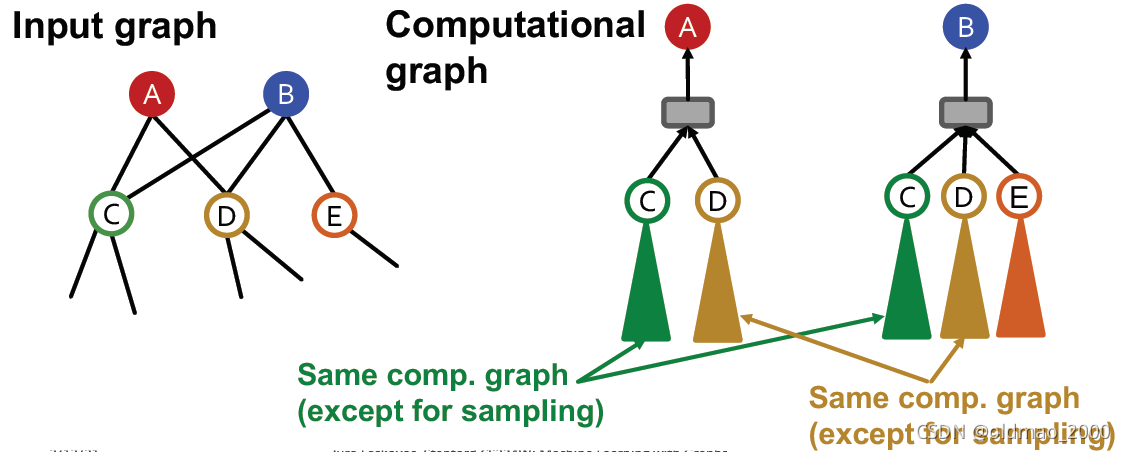
可以看到C和D都是AB的公共邻居,每个都计算了两次,考虑某个大V节点岂不是要计算很多次?
再回头看full-batch GNN的实现过程,所有的节点都用前一层的embedding结果来更新当前层的embedding,不存在上面的重复计算问题:
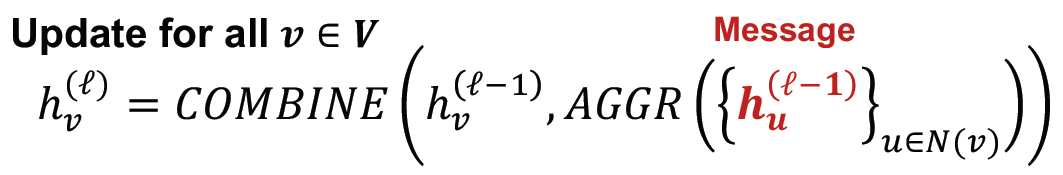
而且,从计算公式可以看到,在每一层的消息汇聚,只用计算
2
×
E
次
,
E
2\times E次,E
2×E次,E是边数量,
u
u
u的消息汇聚给
v
v
v,
v
v
v的消息汇聚给
u
u
u:
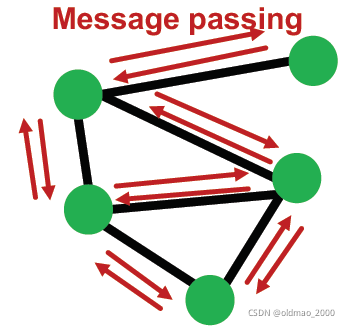
对于
K
K
K层的GNN,那么计算次数为:
2
K
E
2KE
2KE,也就是说整个计算过程的复杂度分别与层数、边数成线性关系,非常快。
也就是说full-batch GNN的layer-wise node embedding update方法可重复使用前一层的embedding结果,不需要冗余的计算和邻居的采样。但是,它的问题在于内存放不下,下面看从full-batch如何解决GNN的大图训练问题。
PS:这里还有另外一个模型HAG,层次化聚合图模型也是类似思想,用的是层次化的划分思想。
Cluster-GCN
子图采样
既然上面讨论了大图有很多优势,但是由于内存方面的限制导致这个方法无法使用,那么可以考虑将大图拆分成可以放进内存的小图,然后再计算的思路:
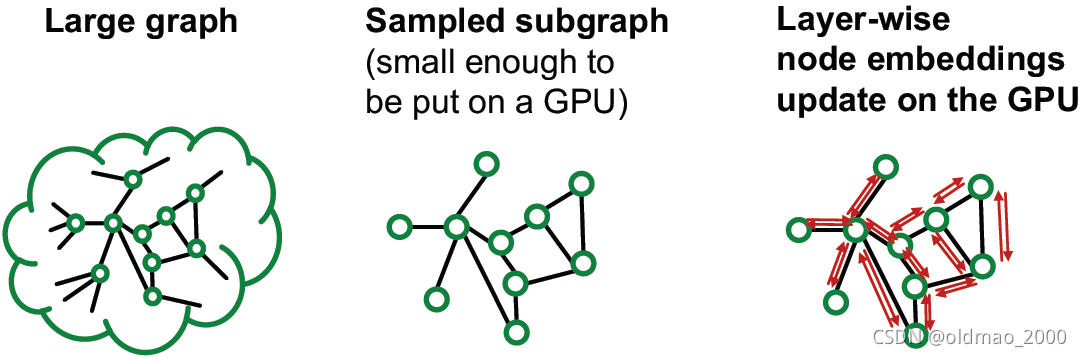
那么这里就稍微看看这个方法的可行性如何,或者说拆分后效果会不会扑街。
由于GNN的计算是基于邻居节点的消息汇聚机制的,那么,如果切分后的子图能够最大限度的保留原图的邻域信息,那么切割后子图消息汇聚产生的embedding和原图应该是差不多的。
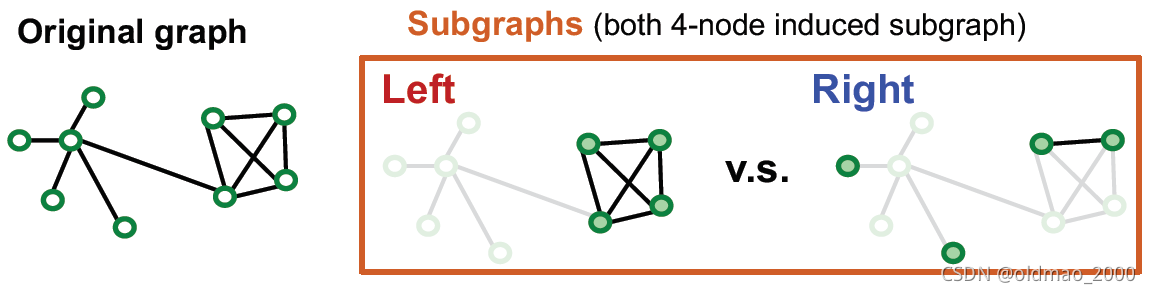
从上面的例子看,在子图采样要最大化保证原来的connectivity,分开但丢边少。
由于现实存在的图中包含较为丰富的社区结构,因此将图中的社区采样出来作为子图,每个子图可以包含原图的local connectivity pattern。
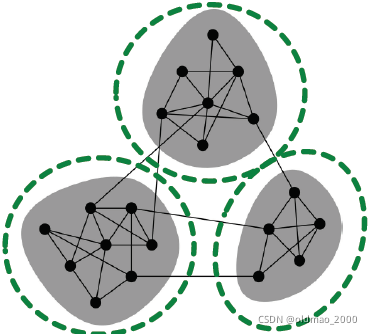
Cluster-GCN overview
给定图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),将其节点
V
V
V划分为
C
C
C个组:
V
1
,
V
2
,
⋯
,
V
C
V_1,V_2,\cdots,V_C
V1,V2,⋯,VC
为了保证社区的完整性,可以使用已有的社区检验方法,例如:Louvain, METIS3。
每个小组的节点
V
1
,
V
2
,
⋯
,
V
C
V_1,V_2,\cdots,V_C
V1,V2,⋯,VC生成对应的
C
C
C个子图:
G
1
,
G
2
,
⋯
,
G
C
G_1,G_2,\cdots,G_C
G1,G2,⋯,GC,每个子图有以下关系:
G
C
≡
(
V
C
,
E
C
)
,
where
E
c
=
{
(
u
,
v
)
∣
u
,
v
∈
V
c
}
G_C\equiv (V_C,E_C),\\ \text{where }E_c=\{(u,v)|u,v\in V_c\}
GC≡(VC,EC),where Ec={(u,v)∣u,v∈Vc}
每个子图之间没有边相连:
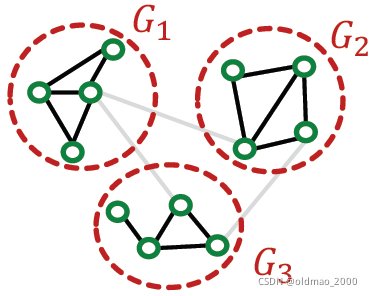
Cluster-GCN: MIni-batch Training
1.对每个mini-batch,随机采样一个节点组:
V
c
V_c
Vc
2.构造induced subgraph:
G
c
=
(
V
c
,
E
c
)
G_c= (V_c,E_c)
Gc=(Vc,Ec)

3.对
G
c
G_c
Gc使用GNN的layer-wise node embedding update(就是对这个子图用full batch的GNN进行计算),得到每个节点的embedding:
h
v
,
v
∈
V
c
h_v,v\in V_c
hv,v∈Vc

4.计算每个节点损失并取平均:
l
s
u
b
(
θ
)
=
1
∣
V
c
∣
⋅
∑
v
∈
V
c
l
v
(
θ
)
l_{sub}(\theta)=\cfrac{1}{|V_c|}\cdot\sum_{v\in V_c}l_v(\theta)
lsub(θ)=∣Vc∣1⋅v∈Vc∑lv(θ)
5.更新参数:
θ
←
θ
−
▽
l
s
u
b
(
θ
)
\theta\leftarrow\theta-\triangledown l_{sub}(\theta)
θ←θ−▽lsub(θ)
Cluster-GCN的问题
Graph community detection algorithm对图进行聚类后,每个社区只包含全部数据中的一小部分
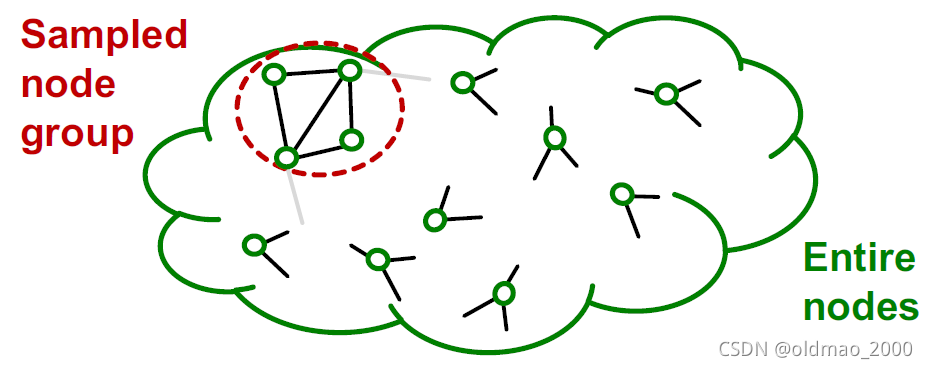
生成的induced subgraph去掉了一些边,准确的说是去掉了社区与社区之间的边,也就是社区之间没有消息的汇聚了,这里就会降低GNN的性能。
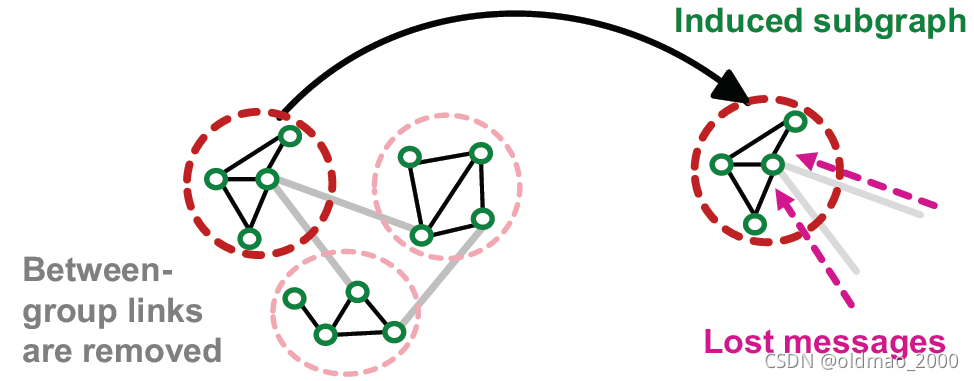
也就是说子图中的节点没有足够的diverse来表达整个图的结构;
此外,由于节点的损失是在每个社区内部计算的,社区到社区的样本分布差异会使得梯度的方差很大,最终导致SGD的收敛性变差。
Cluster-GCN进阶版
对于上面问题的解决方案就是每个mini-batch一次性聚合多个组。
大白话就是大图放不进内存,就想法子切小了放,切太小图被切变样了,性能扑街,现在切不大不小,刚好。
除了切分方式不一样(Sampling multiple node groups),其他计算步骤都一样。
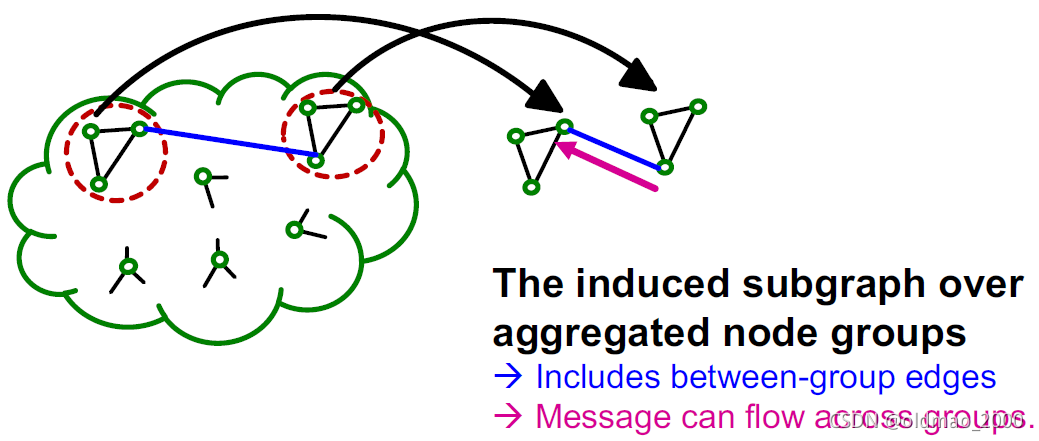
Cluster-GCN进阶版步骤
Pre-processing step:
给定图
G
=
(
V
,
E
)
G=(V,E)
G=(V,E),将其节点
V
V
V划分为
C
C
C个组:
V
1
,
V
2
,
⋯
,
V
C
V_1,V_2,\cdots,V_C
V1,V2,⋯,VC。
这里和原始的Cluster-GCN的划分相比,组的规模要小一些,因为待会要进行组合,单个组太大组合内存会爆。
Mini-batch training:
1.对于每个mini-batch,随机采样属于一个组集合的节点
q
q
q:
{
V
t
1
,
⋯
,
V
t
q
⊂
}
{
V
1
,
V
2
,
⋯
,
V
C
}
\{V_{t_1},\cdots,V_{t_q}\subset\} \{V_1,V_2,\cdots,V_C\}
{Vt1,⋯,Vtq⊂}{V1,V2,⋯,VC}
2.将所有节点组集合中的所有节点进行信息汇聚:(感觉这个步骤应该在后面,这里只是做集合)
V
a
g
g
r
=
V
t
1
∪
⋯
∪
V
t
q
V_{aggr}=V_{t_1}\cup\cdots\cup V_{t_q}
Vaggr=Vt1∪⋯∪Vtq
3.构建induced subgraph
G
a
g
g
r
=
(
V
a
g
g
r
,
E
a
g
g
r
)
where
E
a
g
g
r
=
{
(
u
,
v
)
∣
u
,
v
∈
}
V
a
g
g
r
G_{aggr}=(V_{aggr},E_{aggr})\\ \text{where }E_{aggr}=\{(u,v)|u,v\in \}V_{aggr}
Gaggr=(Vaggr,Eaggr)where Eaggr={(u,v)∣u,v∈}Vaggr
注意,这里的
E
a
g
g
r
E_{aggr}
Eaggr包含组间的边。
后面的步骤略。
时间复杂度比较GraphSAGE vs Cluster-GCN
假定:我们使用
K
K
K成生成
M
(
<
<
N
)
M(<<N)
M(<<N)个节点的embedding。这里
N
N
N是总的节点数量。
基于Neighbor-sampling的GraphSAGE:
如果每层采样
H
H
H个节点,对于每个节点,
K
K
K层计算图共有
H
K
H^K
HK个节点
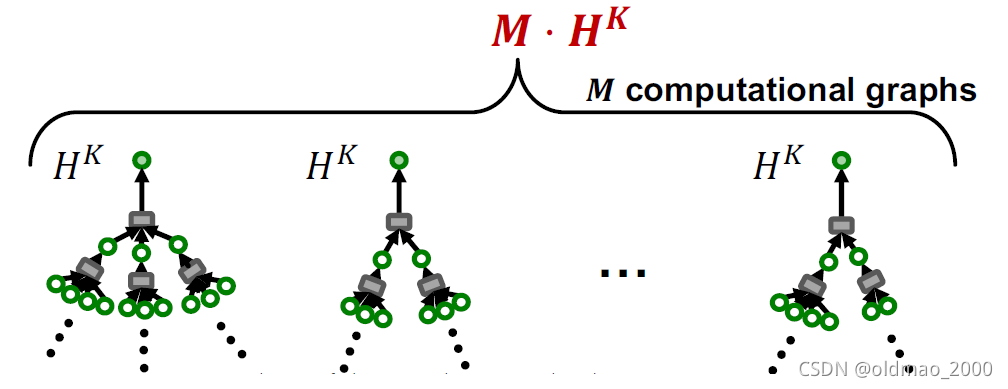
要计算
M
M
M个节点,总的计算量为:
M
⋅
H
K
M\cdot H^K
M⋅HK
Cluster-GCN:
对
M
M
M个节点的induced subgraph执行消息传递,如果子图平均度为:
D
a
v
g
D_{avg}
Davg,那么子图边数量为:
M
⋅
D
a
v
g
M\cdot D_{avg}
M⋅Davg,对于
K
K
K层的消息传递而言,计算量为:
K
⋅
M
⋅
D
a
v
g
K\cdot M\cdot D_{avg}
K⋅M⋅Davg
二者不同量纲无法比较优劣,我们假设
H
=
D
a
v
g
/
2
H=D_{avg}/2
H=Davg/2,也就是采样约50%的邻居,此时Cluster-GCN的计算量为:
2
M
H
K
2MHK
2MHK要远远小于GraphSAGE 的
M
⋅
H
K
M\cdot H^K
M⋅HK
Simplified GCN4
GCN回顾
这块之前有写过一点点笔记,但是重新听了一遍有新的领悟,记录一下。
从简化GCN模型的思路出发,还有FastGCN、 Light GCN,具体看笔记。
先复习一把GCN,这里不写了,直接上GCN的矩阵形式:
记
H
(
k
)
=
[
h
1
(
1
)
⋯
h
∣
V
∣
(
k
)
]
H^{(k)}=[h_1^{(1)}\cdots h_{|V|}^{(k)}]
H(k)=[h1(1)⋯h∣V∣(k)]
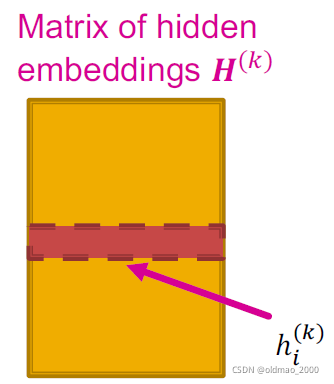
记图的邻接矩阵为
A
A
A,这里的邻接矩阵对角线为1,即包含self-loop
则节点的消息聚合可表示为:
∑
u
∈
N
(
v
)
h
u
(
k
)
=
A
v
,
:
H
(
k
)
\sum_{u\in N(v)}h_u^{(k)}=A_{v,:}H^{(k)}
u∈N(v)∑hu(k)=Av,:H(k)
记度矩阵为对角矩阵
D
D
D:
D
v
,
v
=
Deg
(
v
)
=
∣
N
(
v
)
∣
D_{v,v}=\text{Deg}(v)=|N(v)|
Dv,v=Deg(v)=∣N(v)∣
当然,
D
−
1
D^{-1}
D−1也是对角矩阵:
D
v
,
v
−
1
=
1
∣
N
(
v
)
∣
D_{v,v}^{-1}=\cfrac{1}{|N(v)|}
Dv,v−1=∣N(v)∣1
消息聚合可以写成:
1
∣
N
(
v
)
∣
∑
u
∈
N
(
v
)
h
u
(
k
)
→
矩
阵
形
式
D
−
1
A
H
(
k
)
\cfrac{1}{|N(v)|}\sum_{u\in N(v)}h_u^{(k)}\xrightarrow[]{矩阵形式}D^{-1}AH^{(k)}
∣N(v)∣1u∈N(v)∑hu(k)矩阵形式D−1AH(k)
GCN的中第
v
v
v个节点在第
k
k
k层的embedding可以写为:
h
v
(
k
+
1
)
=
ReLU
(
W
k
1
∣
N
(
v
)
∣
∑
u
∈
N
(
v
)
h
u
(
k
)
)
h_v^{(k+1)}=\text{ReLU}\left(W_k\cfrac{1}{|N(v)|}\sum_{u\in N(v)}h_u^{(k)}\right)
hv(k+1)=ReLU⎝⎛Wk∣N(v)∣1u∈N(v)∑hu(k)⎠⎞
矩阵形式为:
H
(
k
+
1
)
=
ReLU
(
A
~
H
(
k
)
W
k
T
)
where
A
~
=
D
−
1
(1)
H^{(k+1)}=\text{ReLU}(\tilde AH^{(k)}W_k^T)\\ \text{where }\tilde A=D^{-1}\tag1
H(k+1)=ReLU(A~H(k)WkT)where A~=D−1(1)
老师注明了一下:原始版本的
A
~
=
D
−
1
/
2
A
D
−
1
/
2
\tilde A=D^{-1/2}AD^{-1/2}
A~=D−1/2AD−1/2
原始版本的
A
~
\tilde A
A~性能要好,这里为啥?
Simplified GCN简化过程
下面看去掉公式1中的非线性ReLU,并化简:
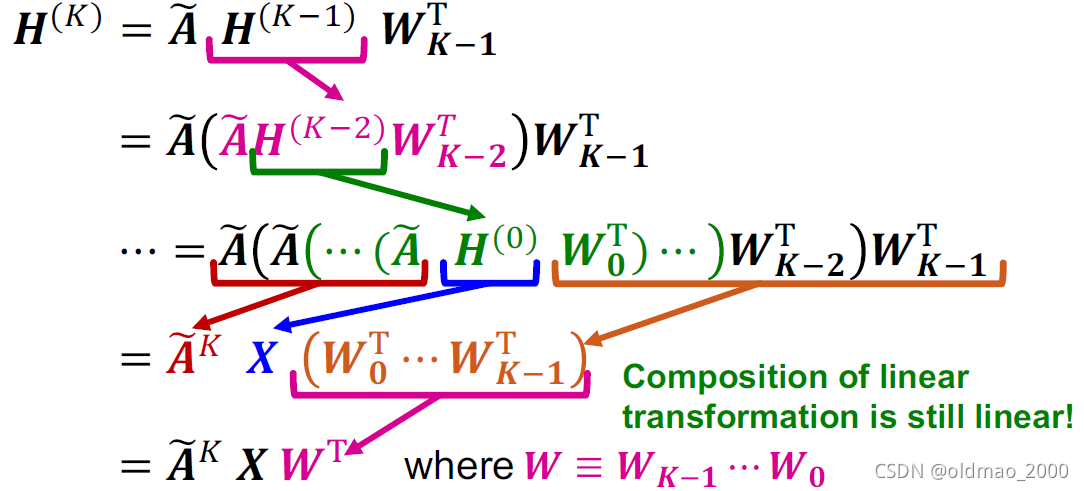
最后结果写成:
H
(
K
)
=
A
~
K
X
W
T
H^{(K)}=\tilde A^KXW^T
H(K)=A~KXWT
由于
A
~
K
X
\tilde A^KX
A~KX不包含可学习的参数,因此它可以提前先算好,这里的这个
A
~
K
\tilde A^K
A~K相当于邻接矩阵的
K
K
K次方,之前有分析过5这个代表
K
K
K阶邻居相连。
这个计算由于是一系列的稀疏矩阵的乘法,非常快。
记
X
~
=
A
~
K
X
W
T
\tilde X=\tilde A^KXW^T
X~=A~KXWT为预先计算好的矩阵,那么矩阵形式就可以写为:
H
(
K
)
=
X
~
W
T
H^{(K)}=\tilde XW^T
H(K)=X~WT
这个形式就是相当于矩阵
X
~
\tilde X
X~的线性变换!对于每个节点的embedding而言:
h
v
(
K
)
=
W
X
~
v
h_v^{(K)}=W\tilde X_v
hv(K)=WX~v
X
~
v
\tilde X_v
X~v是矩阵
X
~
\tilde X
X~中的节点
v
v
v对应的预先计算的特征,就是矩阵中的某一行。整个计算不涉及其他节点,因此,计算出矩阵后
X
~
\tilde X
X~,我们可以并行的计算
M
M
M个节点
{
v
1
,
v
2
,
⋯
,
v
M
}
\{v_1,v_2,\cdots,v_M\}
{v1,v2,⋯,vM}的embedding:
h
v
1
(
K
)
=
W
X
~
v
1
,
h
v
2
(
K
)
=
W
X
~
v
2
,
⋯
h
v
M
(
K
)
=
W
X
~
v
M
.
(2)
h_{v_1}^{(K)}=W\tilde X_{v_1},\\ h_{v_2}^{(K)}=W\tilde X_{v_2},\\ \cdots\\ h_{v_M}^{(K)}=W\tilde X_{v_M}.\tag2
hv1(K)=WX~v1,hv2(K)=WX~v2,⋯hvM(K)=WX~vM.(2)
小结
simplified GCN模型可以分两步:
1.Pre-processing step:先算矩阵
X
~
\tilde X
X~
2.Mini-batch training step:
2.1对每个mini-batch,随机采样
M
M
M个节点
2.2按公式2分别计算每个节点的embedding
3.利用embedding进行预测或者计算Loss
4.使用SGD更新参数
与前面两种思路的比较
相比neighbor sampling:Simplified GCN不用构造计算图,因此生成节点embedding更高效。
相对于Cluster-GCN:Simplified GCN的Mini-batch中的节点是从整个图中进行采样的(各个节点之间的计算没有相互依赖),不需要从子图中进行采样,因此其SGD的方差在训练过程中较小。
存在问题
由于Simplified GCN简化了非线性部分,因此它的表达能力相对于原始GCN是变弱了的。但是在模型的文章中Simplified GCN的表现虽然差,但是并没有差很多,但是效率确实很好。
究其原因,因为图的同质性(Graph homophily),相邻节点(有边连接)通常会趋于相同标签,例如:
在引文网络,存在引用关系的文章一般都是相同领域的文章;
在电影推荐系统,两个好基友通常会喜欢同类型的电影。
Simplified GCN的preprocessing step中,计算的
A
~
K
X
\tilde A^KX
A~KX实际上是不断将其
K
K
K跳邻居特征进行平均后迭代到当前节点上,因此这个也暗自符合了图的同质性,因此Simplified GCN在有同质性的图上效果非常棒,对于那些同质性较差的图,Simplified GCN效果就很扑街。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










