深度之眼Paper带读笔记GNN.08.GCN（上）

前言

本课程来自深度之眼，部分截图来自课程视频。
文章标题：Semi-Supervised Classification with Graph Convolutional Networks
图卷积神经网络的半监督分类（GCN）
作者：Thomas N.Kipf，Max Welling
单位：University of Amsterdam
发表会议及时间：ICLR 2017
公式输入请参考：在线Latex公式

前期知识基础要求

概率论：了解基本的概率论知识，掌握条件概率的概念
图算法：图的基本算法，算法时间复杂度分析
（重点）图频域分析：图的拉普拉斯矩阵、傅里叶变换、图的频域变换、卷积、切比雪夫近似
深度学习：了解SGD等基本原理

论文结构

1. Abstract：提出本文将卷积操作应用到图上，通过图频域的近似分析来建模，学习图的局部结构和节点特征。
2. Introduction：介绍图上节点分类的半监督问题，通过神经网络学习节点的表达，定义了半监督loss function。提出了图上的神经网络信息前向传播规则，并将其与图频域分析联合起来。
3. Fast Approximate Convolutions On Graphs：图的神经网络信息前向传播规则，图频域分析（重点）。
4. Semi-Supervised Node Classification：提出一个两层的GCN模型，并设计了一个半监督的loss function。
5. Related Work：总结了DeepWalk、Node2vec、LINE等算法，GGNN等应用RNN、卷积在图上的算法。
6. Experiments：实验探究模型有效性：节点分类、信息传播、训练时间。（Cora数据集）
7. Discussion：讨论GCN相比其他baselines模型的优势，讨论未来发展方向。
8. Conclusion：总结提出的GCN模型，基于图频域分析的一阶近似，使用图的结构以及节点特征通过半监督学习，实验证明了模型的有效性。

学习目标

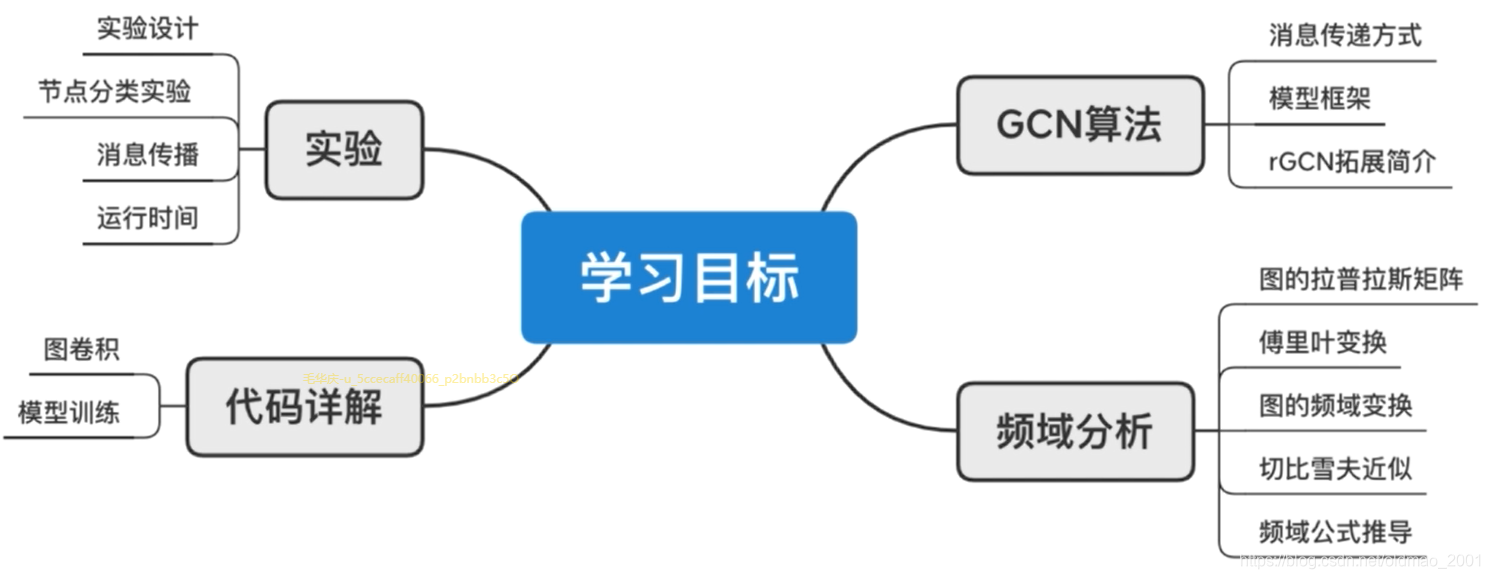
研究背景

直接上图，具体讲解可以参考上一篇笔记

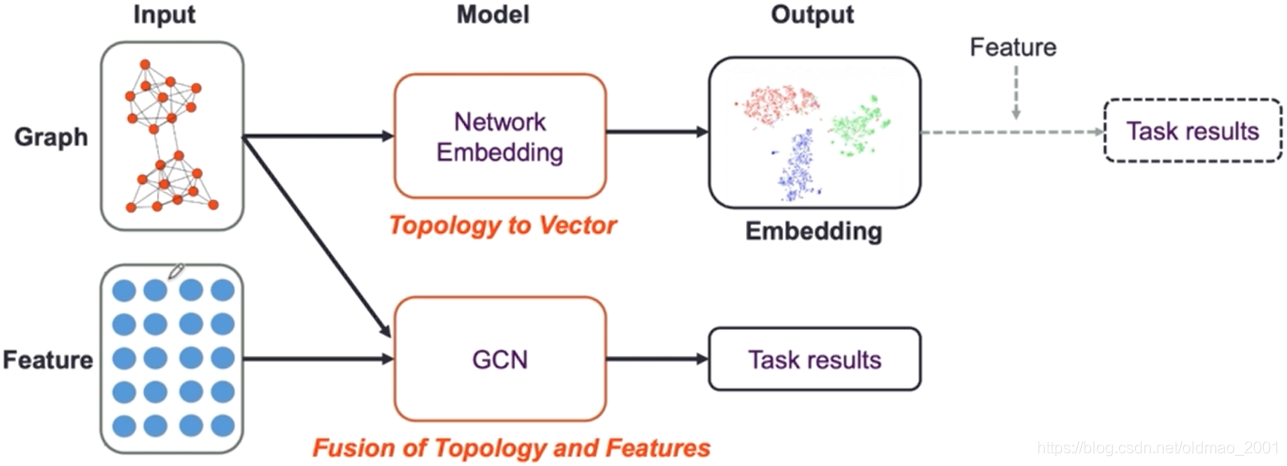
消息传递机制（略，详见上一篇笔记）
前面几篇基于随机游走的论文在获取节点的embedding过程中只考虑了图结构的信息，而节点的特征是在后期加入的，特征并没有经过模型进行抽取或变化；关于6.7.8篇论文除了考虑图本身结构的信息之外，还加入了节点的特征进行计算，因此可以直接完成端到端的任务。


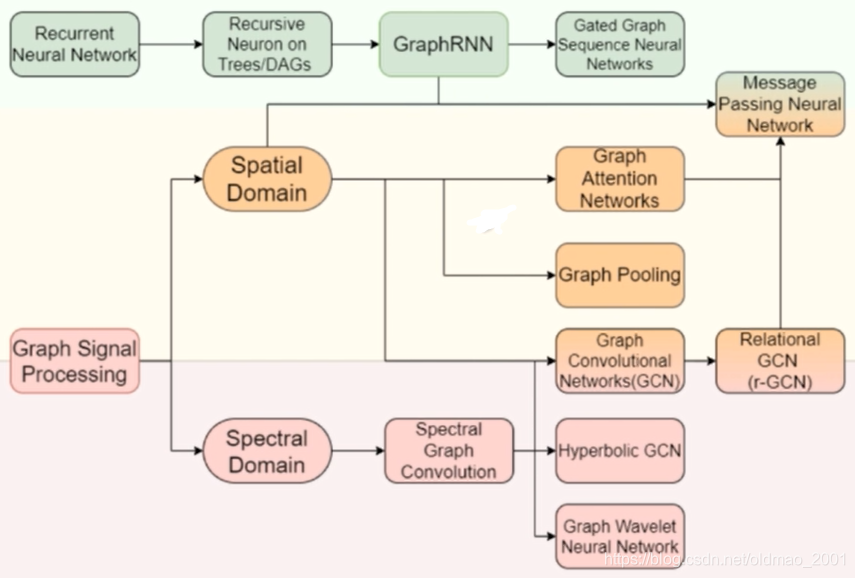
这里面Graph Pooling就相当于GraphSAGE，然后r-GCN是GCN在知识图谱的结合。

研究意义

·图卷积神经网络最常用的几个模型之一（GCN，GAT，GraphSAGE）
·将卷积算法直接用于处理图结构数据，频域分析与消息传播公式
·图频域卷积的局部一阶近似，单层的GCN处理图中一阶邻居的信息，K层GCN处理K阶邻居
·卷积的参数共享，对于每个节点参数是共享的
·图神经网络的最重要模型之一

泛读

摘要

1.本文提出了一种基于图的结构数据的半监督学习框架，该方法可直接在图上进行卷积操作。
2.卷积核的设计是通过图频域分析的局部一阶逼近的计算。
3.本文的模型运行效率高，通过图的局部结构和节点特征来获得节点的向量化表示。
4.大量实验证明了本文方法的有效性。

论文标题

1. Introduction
2. Fast Approximate Convolutions On Graphs
   2.1 Spectral graph convolutions
   2.2 Layer-wise Linear Model
3. Semi-Supervised Node Classification
   3.1 Example
   3.2 Implementation
4. Related Work
   4.1 Graph-based Semi-supervised Learning
   4.2 Neural Networks On Graphs
5. Experiments
   5.1 Datasets
   5.2 Experimental Set-up
   5.3 Baselines
6. Results
   6.1 Semi-supervised Node Classification
   6.2 Evaluation Of Propagation Model
   6.3 Training Time Per Epoch
7. Discussion
   7.1 Semi-supervised Model
   7.2 Limitations And Future Work
8. Conclusion

精读

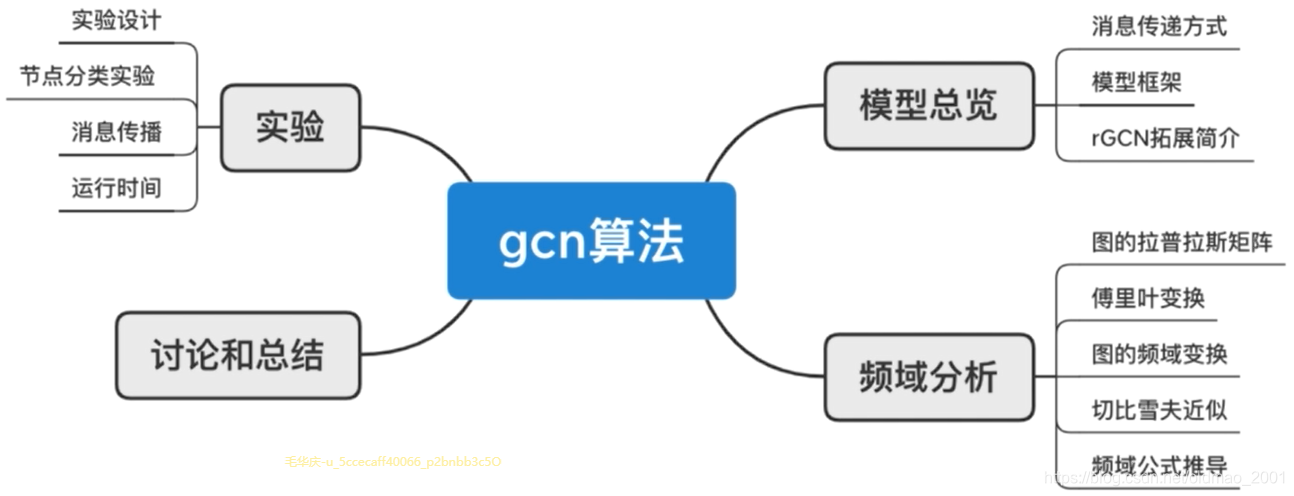
模型总览

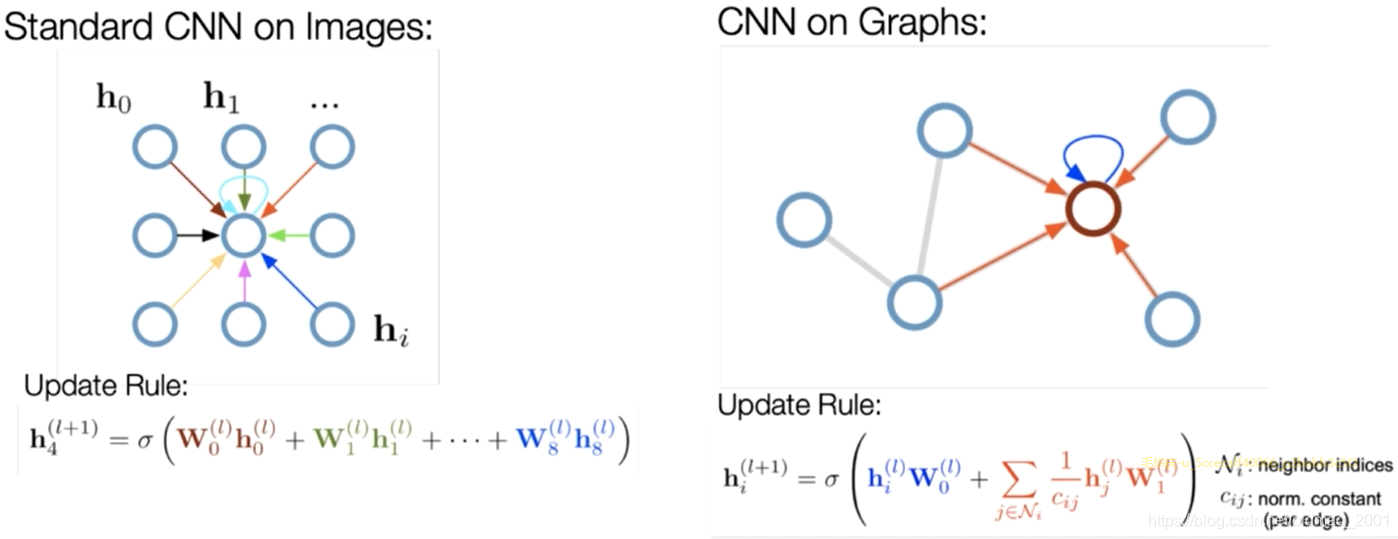
Main idea:pass messages between pairs of nodes & agglomerate. 具体公式为：
$${\text{H}}^{l+1}=\sigma \left({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^l{\Theta }^l\right)\text{\hspace{1em}(1)}$$

这里的两个${\tilde{D}}^{-\frac{1}{2}}$实际上相当于${\tilde{D}}^{-1}$（因为D是对角矩阵），$\tilde{A}$相当于A+I，也就是邻居加上自己本身的信息（I就是对角线都为1的单位阵），$H^l$实际上就是节点的特征矩阵，如果有N个节点，每个节点特征是d维，这个矩阵大小就是N×d，AH如果拿出来看，H的第一列就是特征的第一个维度，上面不为0的项就所有当前节点的邻居节点的特征，AH就得到邻居特征的汇聚效果（由于加了I，这里当然有自己本身的信息）。最后的$\Theta$是我们模型要训练的参数。以上是从空域spatial的角度来理解GCN的，其实前面都有学过，以上讲的一层GCN的操作，如果有多层：
Stacking multiple layers like standard CNNs:
这里的输入是邻接矩阵和特征矩阵X，最后得到的结果要和label进行交叉熵。

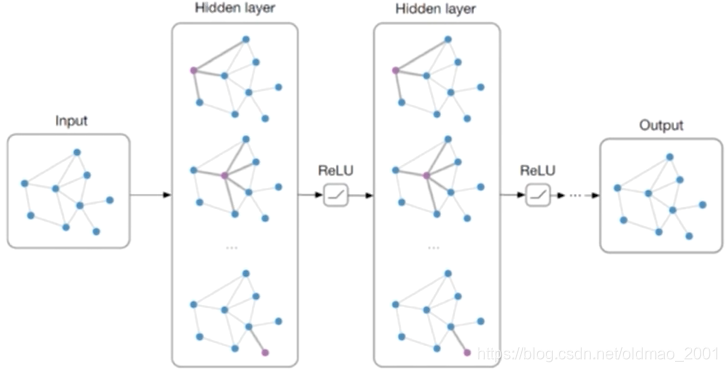
对于GCN的进一步理解如下：Fusing topology and features in the way of smoothing features with the assistance of topology. 就是摘要里面提到的既考虑了图结构信息，又考虑了节点特征信息。

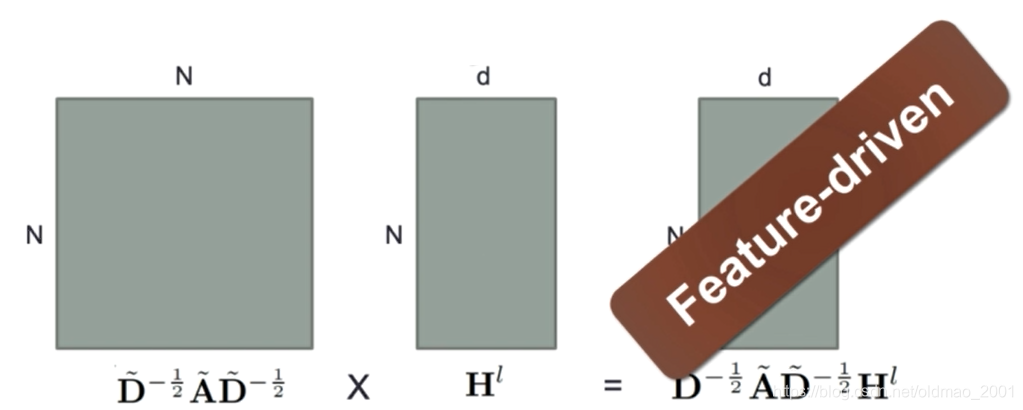
上面的公式1可以拆解如上图所示，第一项里面的三个东西都是N×N的，所以结果还是N×N的（之前的node2vec等随机游走算法都只利用这部分的信息），第一项乘的第二项就是节点的特征融合进来，最后的结果是N×d维的（如图所示可以理解为Feature-driven的模型），公式1中最后乘的$\Theta$相当于对特征矩阵进行投影变换可以把d维变成d’维。

网上例子

假设有这么一个图：

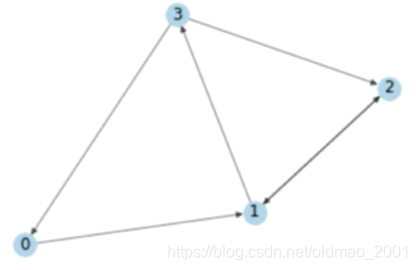
然后我们要根据公式1进行计算，先写出图的邻接矩阵：
$$A=\left[\begin{array}{cccc}0& 1& 0& 0\\ 0& 0& 1& 1\\ 0& 1& 0& 0\\ 1& 0& 1& 0\end{array}\right]$$
然后加上节点本身的信息I（就是对角线为1的单位证）：
$$\tilde{A}=A+I=\left[\begin{array}{cccc}1& 1& 0& 0\\ 0& 1& 1& 1\\ 0& 1& 1& 0\\ 1& 0& 1& 1\end{array}\right]$$
然后图的度矩阵为：
$$\tilde{D}=\left[\begin{array}{cccc}2& 0& 0& 0\\ 0& 3& 0& 0\\ 0& 0& 2& 0\\ 0& 0& 0& 3\end{array}\right]$$
然后两个${\tilde{D}}^{-\frac{1}{2}}$实际上相当于${\tilde{D}}^{-1}$：
$${\tilde{D}}^{-1}=\left[\begin{array}{cccc}\frac{1}{2}& 0& 0& 0\\ 0& \frac{1}{3}& 0& 0\\ 0& 0& \frac{1}{2}& 0\\ 0& 0& 0& \frac{1}{3}\end{array}\right]$$
然后算：
$${\tilde{D}}^{-1}\cdot \tilde{A}=\left[\begin{array}{cccc}\frac{1}{2}& 0& 0& 0\\ 0& \frac{1}{3}& 0& 0\\ 0& 0& \frac{1}{2}& 0\\ 0& 0& 0& \frac{1}{3}\end{array}\right]\left[\begin{array}{cccc}1& 1& 0& 0\\ 0& 1& 1& 1\\ 0& 1& 1& 0\\ 1& 0& 1& 1\end{array}\right]=\left[\begin{array}{cccc}\frac{1}{2}& \frac{1}{2}& 0& 0\\ 0& \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ 0& \frac{1}{2}& \frac{1}{2}& 0\\ \frac{1}{3}& 0& \frac{1}{3}& \frac{1}{3}\end{array}\right]$$
可以看到每行的和为1，达到了一个normalization的效果。
假设图中4个节点的特征维度d=2，则有特征矩阵：
$$H=\left[\begin{array}{cc}0& 0\\ 1& -1\\ 2& -2\\ 3& -3\end{array}\right]$$
最后可以计算出结果（AB两个矩阵的乘积的第m行第n列的元素等于矩阵A的第m行的元素与矩阵B的第n列对应元素乘积之和。）：
$${\tilde{D}}^{-1}\cdot \tilde{A}\cdot H=\left[\begin{array}{cccc}\frac{1}{2}& \frac{1}{2}& 0& 0\\ 0& \frac{1}{3}& \frac{1}{3}& \frac{1}{3}\\ 0& \frac{1}{2}& \frac{1}{2}& 0\\ \frac{1}{3}& 0& \frac{1}{3}& \frac{1}{3}\end{array}\right]\left[\begin{array}{cc}0& 0\\ 1& -1\\ 2& -2\\ 3& -3\end{array}\right]=\left[\begin{array}{cc}\frac{1}{2}& -\frac{1}{2}\\ 2& -2\\ \frac{3}{2}& -\frac{3}{2}\\ \frac{5}{3}& -\frac{5}{3}\end{array}\right]$$

原文例子

原文3.1节也给出了一个例子，一层GCN用的公式为：
$$\hat{A}={\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$$
然后要乘上特征X和第一层参数$W^{(0)}$然后经过ReLU非线性变换，然后经过第二层（第二层的参数是$W^{(1)}$），然后接softmax，如果是Cora数据集应该是7分类：
$$Z=f(X,A)=softmax(\hat{A}ReLU(\hat{A}X{W}^{(0)})W^{(1)})\text{\hspace{1em}(2)}$$
公式2中，第一层的计算为：$ReLU(\hat{A}X{W}^{(0)})$
第一层得到输出结果相当于第二层的输入中的新的特征$X^{\prime }$
因此第二层相当于：$softmax(\hat{A}{X}^{\prime }{W}^{(1)})$
最后得到的Z就是节点的embedding。
所以整个套娃操作就是按照AXW的套路走的。
最后的交叉熵损失函数为：
$$L=-\sum _{l\in {\text{Y}}_L}\sum _{f=1}^F{Y}_{lf}\ln Z_{lf}$$
这里最外面的求和下标代表半监督学习，只取了有label的部分点进行计算，$Y_{lf}$则是代表ground truth，是一个独热编码，第二个求和代表的是softmax操作。

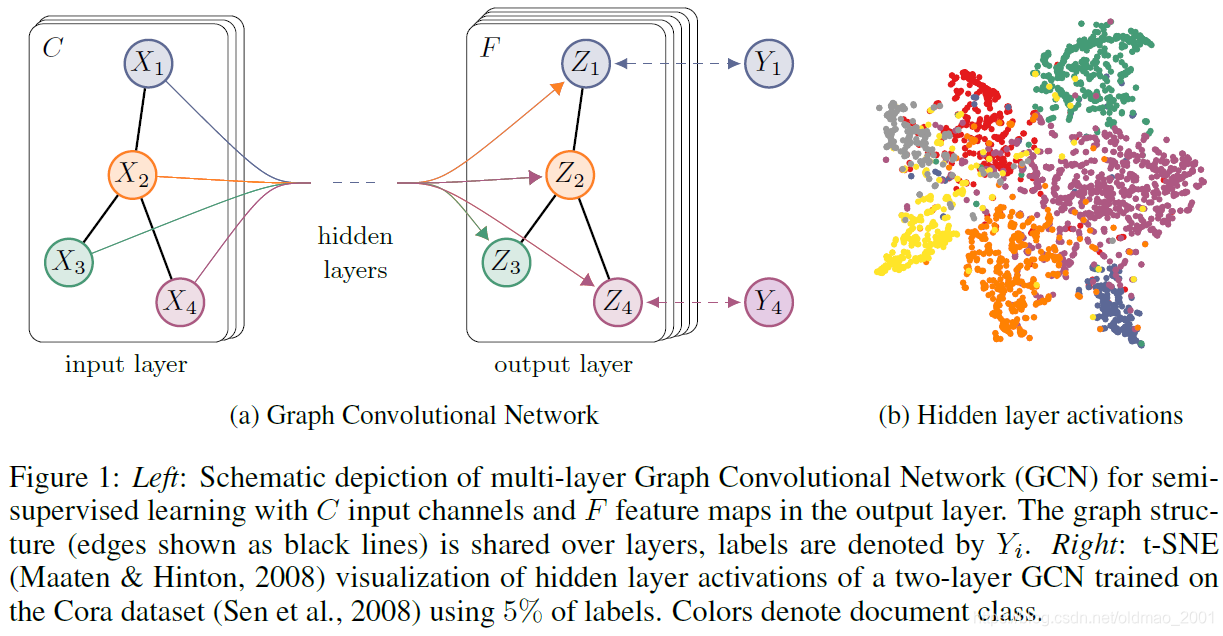
看图加深理解，中间通过两层GCN后输入是C维的，输出是F维的embedding是Z，只有$Z_1$和$Z_4$有标签，只用这两个来计算交叉熵loss

频域和空域Spatial vs Spectral

Two major approaches to build Graph CNNs

1. Spatial Domain: Perform convolution in spatial domain similar to images(euclidean data) with shareable weight parameters.
   · Spatial construction is usually more efficient but less principled.
   · Spatial construction is usually more efficient but less principled.
2. Spectral Domain: Convert Graph data to spectral domain data by using the eigenvectors of laplacian operator on the graph data and perform learning on the transformed data.
   · Spectral construction is more principled but usually slow. Computing Laplacian eigenvectors for large scale data couid be painful.

· Research tries to bridge the gap.(This paper GCN!)

细节一：R-GCN模型结构

这个是用在知识图谱的一个模型，知识图谱一般都是异质图，可以和之前学过的metapath联系起来看一下。
以点$i$在$l+1$层如何从第$l$层计算过来的为例。
$$l_i^{(l+1)}=\sigma \left(\sum _{r\in R}\sum _{j\in N_i^r}\frac{1}{c_{i,r}}{W}_r^{(l)}{h}_j^{(l)}+W_0^{(l)}{h}_j^{(l)}\right)\text{\hspace{1em}(3)}$$
上式3中$W_0^{(l)}$对应是节点自身的参数，$W_r^{(l)}$是邻居节点的参数
$N_i^r$表示点$i$的所有邻居节点的集合，然后r代表邻居节点和当前节点的关系的分类（相当于边的分类），归一化项也体现了，按节点以及邻居类型进行归一化。
可以看到，边的类型越多（邻居节点的类型越多），那么每一层的参数也就越多，例如，我们的邻居类型有10种，那么每一层都有10个$W^{(l)}$参数，所以这里参数还加了下标r。
下面看图，图中的rel表示关系后面的数字代表关系的种类，可以看到对于关系1（rel_1）而言，有六个邻居节点，这里考虑的是有向图，因此还把这六个邻居分成了in和out的两类，下面考虑的关系N也是一样。最后还要加上节点本身的信息（红色那个self-loop）。
原文对这个公式的说明：
where $N_i^r$ denotes the set of neighbor indices of node $i$ under relation $r\in R$. $c_{i,r}$ is a problem-specific normalization constant that can either be learned or chosen in advance (such as $c_{i,r}=|N_i^r|$).

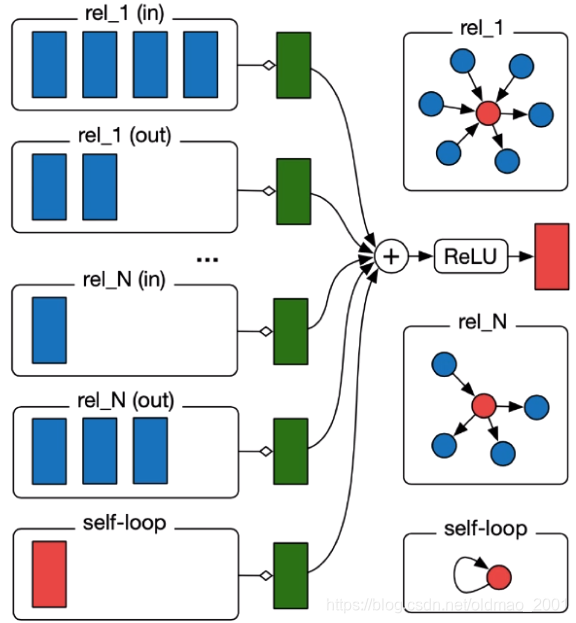
可以看下原文的2.1节
原文在这里：Modeling Relational Data with Graph Convolutional Networks

细节二：拉普拉斯矩阵Laplacian matrix

拉普拉斯算子

参考文献：https://zhuanlan.zhihu.com/p/85287578
拉普拉斯算子（Laplace Operator）是$n$维欧几里得空间中的一个二阶微分算子，定义为梯度（$▽f$）的散度（$▽\cdot$）。
$$\Delta f={▽}^{2}f=▽\cdot ▽f=div(gradf)$$
借用参考文献中的公式：

离散函数的导数可以看做是连续函数的求导（高数中的求极限操作）推导出来的结果。
以上是一维的散度的写法，下面看二维散度的写法，可以看到其中对x求二阶偏导的时候，y是不动的，然后例用上面的一维散度的公式进行展开。

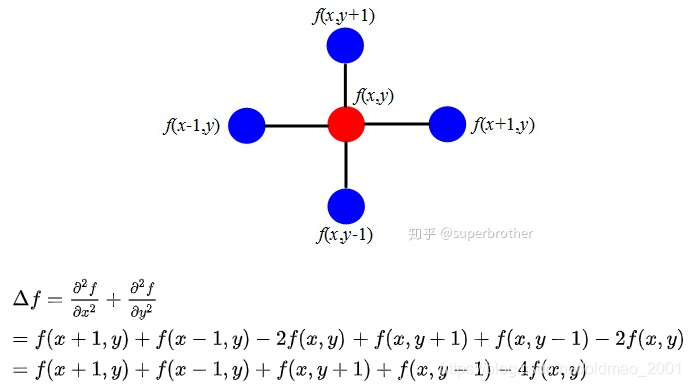
相当于计算红色点与周围四个方向的蓝色点的差的累加和，回过头看一维的拉普拉斯算子就是计算x与其前后点也就是x+1和x-1的差的和

拉普拉斯矩阵

对于图的拉普拉斯算子：
$$\Delta f=\sum _{j\in N_i}(f_i-f_j)$$
相当于求节点i与所有邻居节点之间的差，然后求和。
如果考虑边$E_{ij}$的权重$W_{ij}$的时候：
$$\Delta f_i=\sum _{j\in N_i}{W}_{ij}(f_i-f_j)$$
当$W_{ij}=0$时，表示节点i，j不相邻，可以将非邻居节点的权重剔除，变成：
$$\Delta f_i=\sum _{j\in N}{w}_{ij}(f_i-f_j)$$
展开括号：
$$=\sum _{j\in N}{w}_{ij}{f}_i-\sum _{j\in N}{w}_{ij}{f}_j$$
第一项中$f_i$和求和符合无关，可以只算${\sum }_{j\in N}{w}_{ij}=d_i$，这个就是节点i的度
第二项可以写成向量内积的形式，$w_{i:}=(w_{i1},\cdots ,w_{iN})$是N维行向量；
$f=\left(\begin{array}{c}{f}_1\\ ⋮\\ f_N\end{array}\right)$是N维列向量；
那么图中某个个节点i的拉普拉斯算子就写成了：
$$\Delta f=d_i{f}_i-w_{i:}f$$
对于图中的N个节点：
$$\Delta f=\left(\begin{array}{c}\Delta f_1\\ ⋮\\ \Delta f_N\end{array}\right)=\left(\begin{array}{c}{d}_1{f}_1-w_{1:}f\\ ⋮\\ d_N{f}_N-w_{N:}f\end{array}\right)$$
可以写成一个N×N的矩阵
$$=\left(\begin{array}{ccc}{d}_1& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & d_N\end{array}\right)f-\left(\begin{array}{c}{w}_{1:}\\ ⋮\\ w_{N:}\end{array}\right)f$$
可以写成：
$$diag(d_i)f-Wf=(D-W)f=Lf$$
对于图的拉普拉斯算子的第i项可以写成：
$$(Lf)(i)=\sum _{j\in N_i}{W}_{i,j}[f(i)-f(j)]$$
它的意思就是点i和其所属邻居的差的求和。上式也称为图的拉普拉斯矩阵。
下面来看图的拉普拉斯矩阵的其他定义方式：
D:diagonal matrix whose $i^{th}$ diagnal element $d_i$ is equal to the sum of the weights of all the edges incident to $v_i$
上面定义的拉普拉斯矩阵可以叫：combinatorial graph Laplacian/ non-normalized graph Laplacian:
$$L=D-W\text{\hspace{1em}(4)}$$
下面一种是和GCN中的公式很像的叫：normalized graph Laplacian/ symmetric normalized Laplacian:
$$\tilde{L}=D^{-\frac{1}{2}}L{D}^{-\frac{1}{2}}=I_N-D^{-\frac{1}{2}}W{D}^{-\frac{1}{2}}\text{\hspace{1em}(5)}$$
上式最后那里是把上上个公式的L带到里面并展开的结果。上式中$I_N$是N×N的identity matrix单位矩阵（对角线为1，其他位置都是0的那种矩阵）。
还有一种叫：asymmetric graph Laplacian:
$$L_a=I_N-P\text{\hspace{1em}(6)}$$
其中$P=D^{-1}W$是随机游走矩阵，其每个元素$P_{i,j}$表示图中顶点$v_i$到$v_j$游走（用马尔科夫方法）的概率。
说明：第5和第6分别处理的对称矩阵和非对称矩阵的情况。
下面看一下拉普拉斯矩阵的公式4的每个位置取值，这里我们假设所有边的权重都是1，那么就意味在W就是邻接矩阵，有边相连的位置就是1，否则就是0。那么拉普拉斯矩阵某个位置的取值为：
$$L(u,v)=\{\begin{array}{ll}& d_v\text{if }u=v(d_v\text{ is the degree of node }v)\\ & -1\text{ if }u\ne v,(u,v)\in E\\ & 0\text{ otherwise }\end{array}\text{\hspace{1em}(7)}$$
第一种情况，当$u=v$，这个时候就是指的同一个节点的情况，那么邻接矩阵这个位置为0，因此只有$d_v$这项；
第二种情况，当$u\ne v,(u,v)\in E$，这个时候表明u和v是两个不同节点，而且二者有边相连，那么这个时候其邻接矩阵的这个位置值为1，但是在度矩阵D中，肯定是不在对角线上，因此D这项为0（度矩阵只有对角线上有值，该值为该节点的度），因此0-1=-1，最后结果就是-1；
第三种情况，u和v没有边相连，邻接矩阵位置上值为0，也不在D的对角线上，D也为0，最后结果就是0.
对于公式5，拉普拉斯矩阵的取值为：
$$\tilde{L}(u,v)=\{\begin{array}{ll}& 1\text{if }u=v,d_v\ne 0(d_v\text{ is the degree of node }v)\\ & -\frac{1}{\sqrt{d_u{d}_v}}\text{ if }u\ne v,(u,v)\in E\\ & 0\text{ otherwise }\end{array}\text{\hspace{1em}(8)}$$
公式5可以理解为对公式4除以一个$d_v$进行归一化，因此就是把上式7每种情况除一个$d_v$就ok了。

拉普拉斯矩阵的性质

一般化的拉普拉斯矩阵（generalized graph Laplacians）：归一化normalized和非归一化non-normalized的拉普拉斯矩阵都可以统称为generalized graph Laplacians.
1.对于generalized graph Laplacians，如果图中两个顶点有边相连，则矩阵对应位置为负值（情况二），如果两个顶点没有边相连，则矩阵对应位置为0（情况三），如果是对角线（同一个节点），那么取值可以是任意实数（情况一）
2.对于$L$和$\tilde{L}$都有相同的特征值，这个很重要，要对矩阵进行特征分解才能得到图频域的结果。
3.图的拉普拉斯矩阵还可以叫：admittance matrix, discrete Laplacian or Kirchohoff matrix.
4.对于某个图的拉普拉斯矩阵要使用归一化normalized或非归一化non-normalized的形态，并没有明确规定。

拉普拉斯矩阵例子

An example of non-normalized $L$ with $W=A$,$L=D-A$:

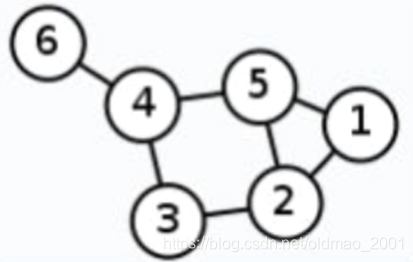
度矩阵：
$$D=\left(\begin{array}{cccccc}2& 0& 0& 0& 0& 0\\ 0& 3& 0& 0& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 0& 0& 0& 3& 0& 0\\ 0& 0& 0& 0& 3& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right)$$
邻接矩阵：
$$A=\left(\begin{array}{cccccc}0& 1& 0& 0& 1& 0\\ 1& 0& 1& 0& 1& 0\\ 0& 1& 0& 1& 0& 0\\ 0& 0& 1& 0& 1& 1\\ 1& 1& 0& 1& 0& 0\\ 0& 0& 0& 1& 0& 0\end{array}\right)$$
拉普拉斯矩阵（没有归一化的）：
$$L=D-A\left(\begin{array}{rrrrrr}2& -1& 0& 0& -1& 0\\ -1& 3& -1& 0& -1& 0\\ 0& -1& 2& -1& 0& 0\\ 0& 0& -1& 3& -1& -1\\ -1& -1& 0& -1& 3& 0\\ 0& 0& 0& -1& 0& -1\end{array}\right)$$

细节三：图的频域变换

图的拉普拉斯矩阵性质：
(normalized/non-normalized)graph Laplacian($L$,or $\tilde{L}$)is a real symmetric matrix(看例子就知道，拉普拉斯矩阵是一个对称矩阵), with a complete set of orthonormal eigenvectors（并且有一组正交特征向量）, which we denote by { u l } \{u_l\} {ul​} where $l=0,1,\cdots ,N-1$.
其中 { u l } \{u_l\} {ul​}对应一个非负实数特征值 { λ l } \{\lambda_l\} {λl​}
因此，根据线性代数的性质可知：
$$L{u}_l={\lambda }_l{u}_l\text{\hspace{1em}(9)}$$
图有多少个连通分量则有多少个特征值等于0。对于一个连通图，则只有一个特征值为0。
因此对于一个连通图，所有的特征值可以做如下排列：
$$0={\lambda }_0\le {\lambda }_1\cdots \le {\lambda }_{N-1}$$
整个特征值可以表示为：
σ ( L ) = { λ 0 , λ 1 , ⋯   , λ N − 1 } \sigma(L)=\{\lambda_0,\lambda_1,\cdots,\lambda_{N-1}\} σ(L)={λ0​,λ1​,⋯,λN−1​}
拉普拉斯矩阵的特征分解也可以写成矩阵的形式：
$$L=U\left(\begin{array}{cccc}{\lambda }_0& 0& \cdots & 0\\ 0& {\lambda }_1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_{N-1}\end{array}\right)U^{-1}=U\left(\begin{array}{cccc}{\lambda }_0& 0& \cdots & 0\\ 0& {\lambda }_1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & {\lambda }_{N-1}\end{array}\right)U^T$$
上式中${\lambda }_i$是特征值，$U=(\overrightarrow{u_0},\overrightarrow{u_1},\cdots ,{\vec{u}}_{N-1})$（这里下标是从0开始，后面一小节下标从1开始，总的维度都是N）, $\overrightarrow{u_i}$是列向量，并且是单位特征向量，$U^{-1}$可写成$U^T$（因为$U{U}^T=I_N$，二者是正交向量）。
如果对输入信号$f_{in}$做拉普拉斯变化，就是：
$$f_{out}=\hat{h}(L)f_{in}$$
其中
$$\hat{h}(L)=U\left(\begin{array}{cccc}\hat{h}({\lambda }_0)& 0& \cdots & 0\\ 0& \hat{h}({\lambda }_1)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & \hat{h}({\lambda }_{N-1})\end{array}\right)U^T$$
关于特征向量看这里、矩阵分解可以看这里。

图的频域变换Graph spectral

将图的拉普拉斯变换和图的频域变换做一个类比。
傅里叶变换（将信号从时域变换到频域）：
$$X(f)={\int }_{-\infty }^{\infty }x(t)e^{-j2\pi ft}dt$$
反向傅里叶变换：
$$x(t)={\int }_{-\infty }^{\infty }X(f)e^{j2\pi ft}df$$
总体可以写成：
$$x(t)\rightleftharpoons X(f)$$
其中$2\pi f=\omega$
拉普拉斯算子可以理解成一种变换
上面我们推出来的公式9可以写成：
$$Av=\lambda v\text{\hspace{1em}(10)}$$
将拉普拉斯算子与傅里叶变换中的e那项相乘（这一步结果可以参考拉普拉斯算子的定义，就是求散度，二阶导数）：
$$\Delta e^{-i\omega t}=\frac{{\partial }^2}{\partial t^2}{e}^{-i\omega t}$$
对上面的复合函数求导得：
$$\Delta e^{-i\omega t}=-{\omega }^2{e}^{-i\omega t}\text{\hspace{1em}(11)}$$
对比公式10公式11中可以看到：
10中的特征向量$v$相当于11中的$e^{-i\omega t}$；
10中的拉普拉斯矩阵$A$相当于11中的$\Delta$；
10中的特征值$\lambda$相当于11中的${\omega }^2$。
因此，图信号到图频域的变换就可以写为：
$$F({\lambda }_l)=\hat{f}({\lambda }_l)=\sum _{i=1}^{N}f(i)u_l^{\ast }(i)\text{\hspace{1em}(12)}$$
反过来：
$$f(i)=\sum _{l=1}^N\hat{f}({\lambda }_l)u_l(i)\text{\hspace{1em}(13)}$$
公式12可以写成矩阵的形式：
$$\left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_N)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_1(2)& \cdots & u_1(N)\\ u_2(1)& u_2(2)& \cdots & u_2(N)\\ ⋮& ⋮& \ddots & ⋮\\ u_N(1)& u_N(2)& \cdots & u_N(N)\end{array}\right)\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(N)\end{array}\right)$$
然后写成向量的形式：
$$\hat{f}=U^{T}f$$
同理，公式13可以写成矩阵的形式：
$$\left(\begin{array}{c}f(1)\\ f(2)\\ ⋮\\ f(N)\end{array}\right)=\left(\begin{array}{cccc}{u}_1(1)& u_1(2)& \cdots & u_1(N)\\ u_2(1)& u_2(2)& \cdots & u_2(N)\\ ⋮& ⋮& \ddots & ⋮\\ u_N(1)& u_N(2)& \cdots & u_N(N)\end{array}\right)\left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_N)\end{array}\right)$$
然后写成向量的形式：
$$f=U^T\hat{f}$$

图频域变换证明

通常图频域变换的公式写为：
$$(f\ast h{)}_G=U((U^{T}h)\odot (U^{T}f))\text{\hspace{1em}(14)}$$
里面是两个图转频域的变化进行点乘，然后再转换回图。
下面证明公式14与下式等价
$$(f\ast h{)}_G=U\left(\begin{array}{ccc}\hat{h}({\lambda }_1)& & \\ & \ddots & \\ & & \hat{h}({\lambda }_n)\end{array}\right)U^{T}f\text{\hspace{1em}(15)}$$
我们将图信号记为一个列向量：
$$f=\left(\begin{array}{c}h(1)\\ h(2)\\ ⋮\\ h(n)\end{array}\right)$$
另外一个图信号，实际上是图卷积的卷积核，可以记为：
$$h=\left(\begin{array}{c}h({\lambda }_1)\\ h({\lambda }_2)\\ ⋮\\ h({\lambda }_n)\end{array}\right)$$
将上面两个信号通过下面两个式子进行变化，得到图频域信号：

$$\hat{f}({\lambda }_l)=\sum _{i=1}^{N}f(i)u_l(i),\hat{h}({\lambda }_l)=\sum _{i=1}^{N}h(i)u_l(i)$$
堆叠写成矩阵的形式：
$$\hat{f}=U^{T}f,\hat{h}=U^{T}h$$
最后频域信号可以写为：
$$\hat{f}=\left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_n)\end{array}\right),\hat{h}=\left(\begin{array}{c}\hat{h}({\lambda }_1)\\ \hat{h}({\lambda }_2)\\ ⋮\\ \hat{h}({\lambda }_n)\end{array}\right)$$

比较公式14和15，右边第一项是U，要证明的就是后面部分要相等：
$$\left(\begin{array}{ccc}\hat{h}({\lambda }_1)& & \\ & \ddots & \\ & & \hat{h}({\lambda }_n)\end{array}\right)U^{T}f=(U^{T}h)\odot (U^{T}f)$$
上式中左边的$U^{T}f$，实际上就是把$f$转换为频域$\hat{f}$，把上面求出的频域结果带过来，左边可以写为：
$$\left(\begin{array}{ccc}\hat{h}({\lambda }_1)& & \\ & \ddots & \\ & & \hat{h}({\lambda }_n)\end{array}\right)U^{T}f=\left(\begin{array}{ccc}\hat{h}({\lambda }_1)& & \\ & \ddots & \\ & & \hat{h}({\lambda }_n)\end{array}\right)\hat{f}=\left(\begin{array}{ccc}\hat{h}({\lambda }_1)& & \\ & \ddots & \\ & & \hat{h}({\lambda }_n)\end{array}\right)\left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_n)\end{array}\right)\text{\hspace{1em}(16)}$$
同理，右边也是将$f$转换为频域$\hat{f}$，$h$转换为频域$\hat{h}$：
$$(U^{T}h)\odot (U^{T}f)=\hat{h}\odot \hat{f}=\left(\begin{array}{c}\hat{h}({\lambda }_1)\\ \hat{h}({\lambda }_2)\\ ⋮\\ \hat{h}({\lambda }_n)\end{array}\right)\odot \left(\begin{array}{c}\hat{f}({\lambda }_1)\\ \hat{f}({\lambda }_2)\\ ⋮\\ \hat{f}({\lambda }_n)\end{array}\right)\text{\hspace{1em}(17)}$$
公式16的矩阵相乘与点乘结果是一样的，因为第一个矩阵除了对角线都是0。

小结

Starting from signal processing:
Recall that: The Laplacian is indeed diagonalized by the Fourier basis (the orthonormal eigenvectors) $U=[u_0,u_1,\dots ,u_{N-1}]\in R^{N\times N}$.
拉普拉斯矩阵实际上就是傅里叶基（就是一组正交特征向量），上式中是拉普拉斯矩阵的N个特征向量

Let $\Lambda =diag([{\lambda }_0,\cdots ,{\lambda }_{N-1}])$, then we have $L=U\Lambda U^T$.
如果将特征值写成对角线矩阵，则拉普拉斯特征变化就可以写成上面的式子。

The graph Fourier transform of a signal $x\in R^N$ is then defined as $\hat{x}{U}^{T}x\in R^N$, with inverse $x=U\hat{x}$. This transformation enableds the formation of fundamental operations. such as filtering, just as on Euclidean spaces.
图的频域变换和图的频域反变化如上面两个公式所示。
Recall that:
$$X\otimes Y=Fourie{r}_{inverse}(Fourier(X)\odot Fourier(Y))$$
就是公式14
Definition of convolutional operator:
$$(f\ast h{)}_{\ast \mathfrak{g}}=U((U^{T}h)\odot (U^{T}f))$$

未完，点我看下篇