番外.李宏毅学习笔记.ST1.Introduction

公式输入请参考： 在线Latex公式
PPT

Structured Learning

我们学过的DL,SVM等，输入和输出都是向量，但是，有的时候，我们想要输入的不是一个向量，按照OO的思想来讲，我想要输入一个对象，如：输入树形结构，输出也是一个树形结构。
$$f:X\to Y$$
这里的X和Y不再局限于向量，而是对象。
Xis the space of one kind of obiect. Y is the space of another kind of object.
· We need a more powerful function $f$
· Input and output are both objects with structures
· Object: sequence, list, tree, bounaing box……

Example Application

· Speech recognition
·X: Speech signal(sequence)>Y: text(sequence)
· Translation
·X: Mandarin sentence(sequence)->Y: English sentence(sequence)
· Syntactic Paring
·X: sentence>Y: parsing tree(tree structure)
· Object Detection
·X: Image->Y: bounding box
· Summarization
·X: long document.>Y: summary(short paragraph)
· Retrieval
·X: keyword ->y: search result(a list of webpage)
看上去ST貌似很麻烦，实际上ST有一个统一的框架：

Unified Framework

Training
找到一个函数$F$，这里和之前不一样，之前都是找$f$
函数$F$的输入是$X$和$Y$，输出是一个实数$R$。
$F(x,y)$是衡量输入$X$和$Y$之间有多匹配，匹配度（compatible）越高，输出值越大
Inference(Testing)
给定一个对象X，目标是：
$$\tilde{y}=arg\underset{y\in Y}{\max }F(x,y)$$
上节中的函数$f$，是输入$X$，输出$Y$：$f:X\to Y$，结合上面的式子：
$$f(x)=\tilde{y}=arg\underset{y\in Y}{\max }F(x,y)$$
不知道为什么？没关系，看个例子：

Unified Framework-Object Detection

·Task description
·Using a bounding box to highlight the position of a certain object in an image.
输入$X$：图像，输出$Y$：边界框
例如：

貌似叫凉宫春日？

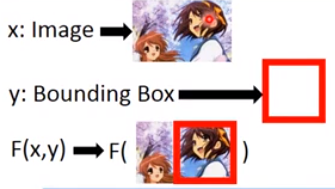
按框架的讲法：

$F(x,y)$是衡量框和人物的匹配度。


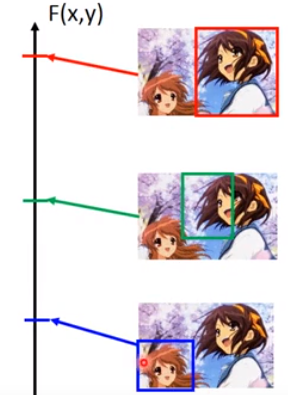
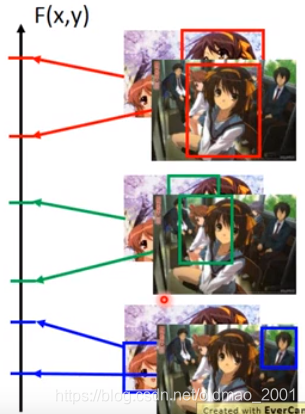
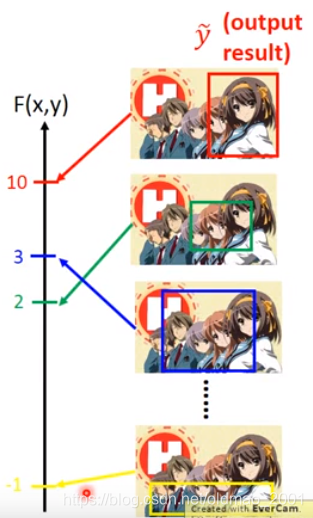
testing的时候就是找一张含有图片。

然后穷举所有框框有可能出现的地方。然后看哪个框框的得分最高

Unified Framework-Summarization

·Task description
·Given a long document
·Select a set of sentences from the document,and cascade the sentences to form a short paragraph.
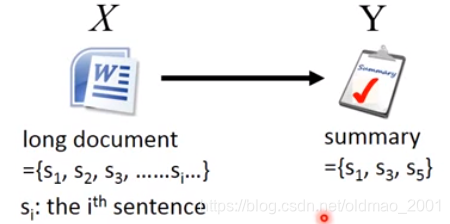
输入是一个长文档 X = { s 1 , s 2 , s 3 , . . . s i , . . . } X=\{s_1,s_2,s_3,...s_i,...\} X={s1​,s2​,s3​,...si​,...}，其中$s_i$表示文档中第$i$个句子。
输出是一个总结 Y = { s 1 , s 3 , s 5 3 } Y=\{s_1,s_3,s_53\} Y={s1​,s3​,s5​3}

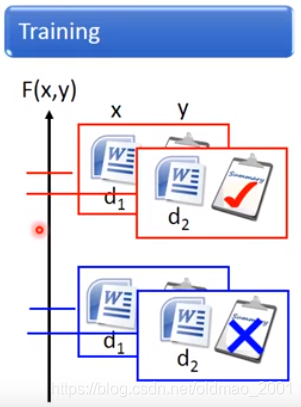
训练：当文档与总结配对的时候$F(x,y)$的值很大

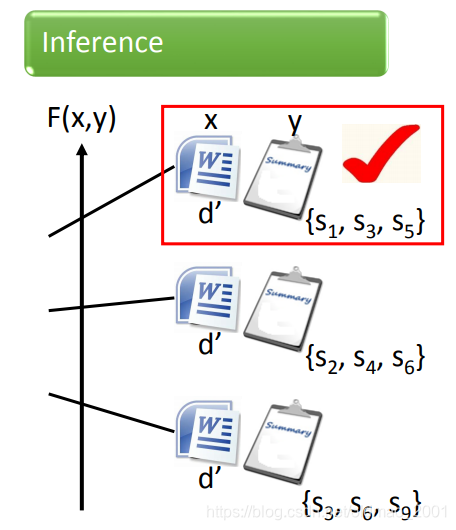
testing的时候，穷举所有的总结，看哪个总结配上文档$F(x,y)$值最大。

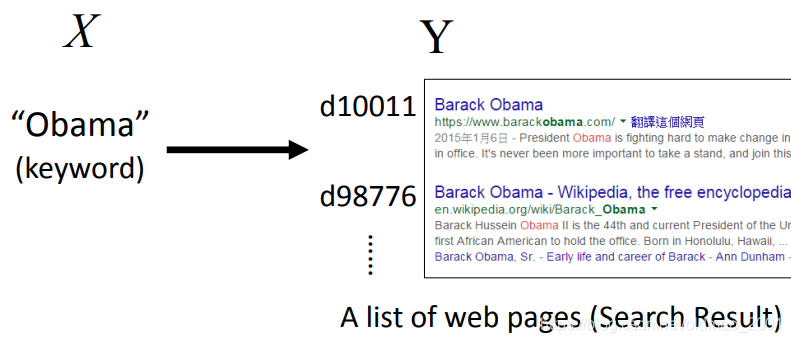
Unified Framework-Retrieval

·Task description
·User input a keyword $Q$
·System returns a $list$ of web pages
输入是查询词，输出是查询的结果

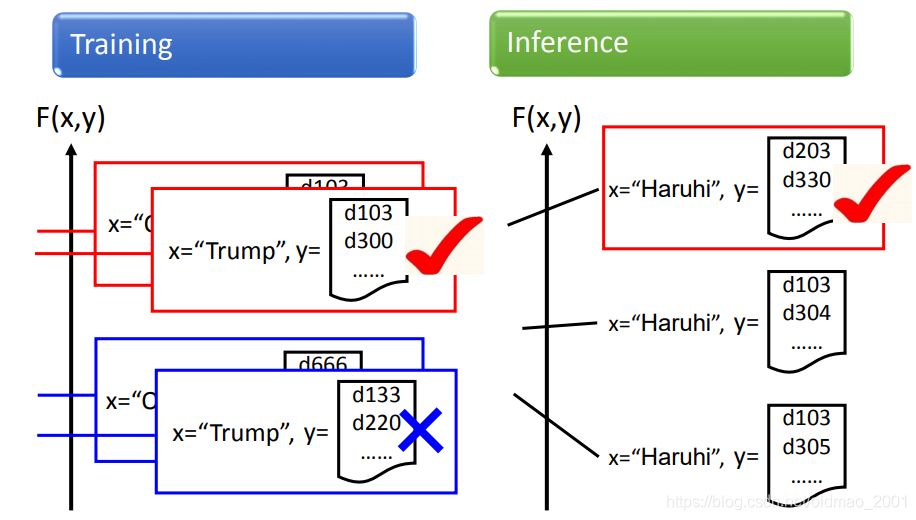
Unified Framework的统计学角度理解

训练：
估计两个对象$X$和$Y$的联合分布概率，记为$P(x,y)$：
$$P:X\times Y\to [0,1]$$
testing就是：
给定x的条件下，求y出现的最大概率
$$\tilde{y}=arg\underset{y\in Y}{\max }P(y|x)=arg\underset{y\in Y}{\max }\frac{P(x,y)}{P(x)}$$
由于分母和y求最大值没有关系，所以分母可以去掉
$$\tilde{y}=arg\underset{y\in Y}{\max }P(x,y)$$
这样就和前面讲的对应起来了：

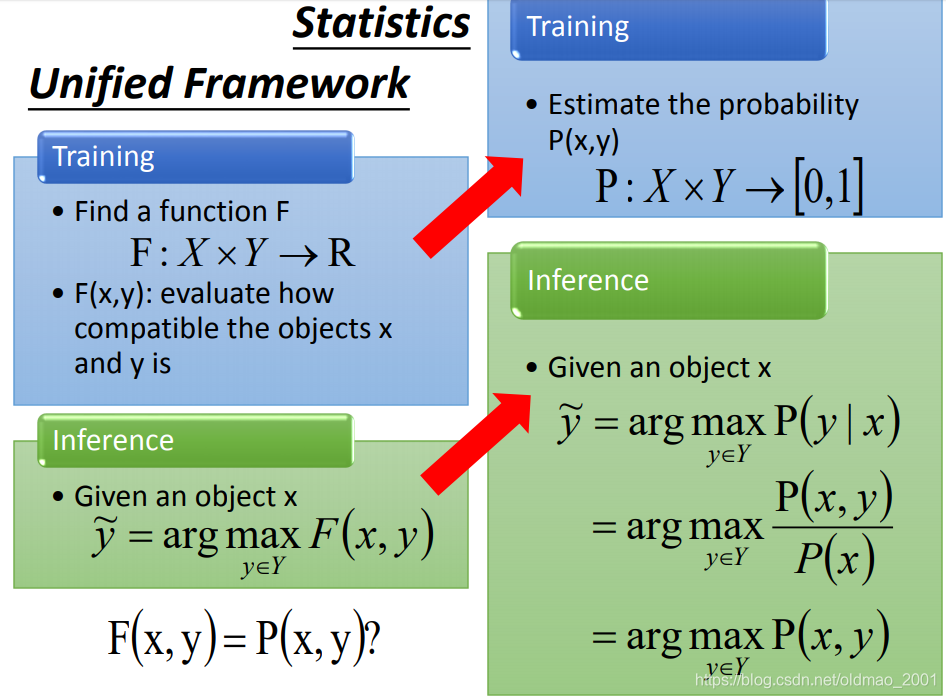
最下面的问号意思是：之前的$F(x,y)$是求xy的匹配度，$P(x,y)$是求xy的联合概率，这里两个事情是不是一样？？理论上是一样的
但是统计学上有如下缺点：
·Probability cannot explain everything
·0-1constraint is not necessary. 很多对象是高维的，加这个限制就要做normalization，花费太大精力，没有必要。
好处就是：容易理解。
Energy-based Model:这个是立坤大佬提出的模型，实际上也是ST。
http://www.cs.nyu.edu/~yann/research/ebm/

Unified Framework的三个问题

问题一

很难想象$F(x,y)$是什么样子
·Evaluation:What does $F(x,y)$ look like?
·How $F(x,y)$ compute the "compatibility"of objects $x$ and $y$

问题二

在testing阶段如何求解最大值问题。
·Inference:How to solve the “arg max” problem
$$\tilde{y}=arg\underset{y\in Y}{\max }F(x,y)$$
The space Y can be extremely large!
Object Detection:Y=All possible bounding box(maybe tractable)这个就有无穷多个组合。。。
Summarization:Y=All combination of sentence set in a document …
Retrieval: Y=All possible webpage ranking ….

问题三

Training: Given training data, how to find $F(x,y)$
我们有的训练数据：
{ ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , . . . , ( x r , y ^ r ) , . . . } \{(x^1,\widehat y^1),(x^2,\widehat y^2),...,(x^r,\widehat y^r),...\} {(x1,y ​1),(x2,y ​2),...,(xr,y ​r),...}
我们要训练$F(x,y)$，使得正确匹配的$(x,\hat{y})$的得分要高于其他(x,y)，这个训练过程是非常难以完成。

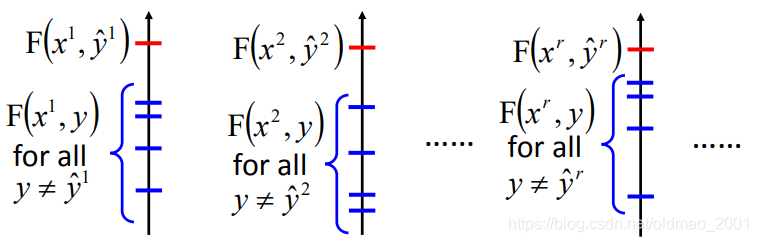
小结

要下课了，后面提示这三个问题要用GAN解决。