本文深入讲解了梯度下降法、牛顿法及其收敛速度，涵盖了无约束优化问题的解决策略，对比了不同优化方法的优劣，适用于机器学习和深度学习领域的算法优化。
本课程来自 深度之眼，部分截图来自课程视频。
【第四章 最优化理论】4.1无约束最优化
在线LaTeX公式编辑器
任务详解：
这节课主要介绍了梯度下降法，牛顿法，牛顿法收敛速度等知识点。
掌握目标：
1、掌握梯度下降法
2、了解牛顿法，拟牛顿法
3、了解梯度下降和牛顿法的收敛速度以及优缺点
无约束优化(用得最多)
无约束优化问题是机器学习中最普遍、最简单的优化问题。
x
∗
=
m
i
n
x
f
(
x
)
,
x
∈
R
n
x^*=min_xf(x),x\in R^n
x∗=minxf(x),x∈Rn
求最大值也可以 在前面加上负号，变成上面求最小的形式。
梯度下降法
求一个函数f(x)的最小值一般有两种方式：
①对函数f(x)求导并使其等于0(或者说使得梯度
▽
f
(
x
)
\triangledown f(x)
▽f(x)等于0)，但是很多复杂的函数求导后没法求出解，所以这种方法实际上很少用。
② 基于迭代的方法，从某个点
x
0
x_0
x0开始找很多点
x
0
→
x
1
→
x
2
⋯
x_0\to x_1\to x_2\cdots
x0→x1→x2⋯，使得这些点满足：
f
(
x
0
)
>
f
(
x
1
)
>
f
(
x
2
)
⋯
f(x_0)> f(x_1)> f(x_2)\cdots
f(x0)>f(x1)>f(x2)⋯，且有
x
1
=
x
0
−
λ
▽
f
(
x
0
)
∣
▽
f
(
x
0
)
∣
x_1=x_0-\lambda\cfrac{\triangledown f(x_0)}{|\triangledown f(x_0)|}
x1=x0−λ∣▽f(x0)∣▽f(x0)，这里
▽
f
(
x
0
)
∣
▽
f
(
x
0
)
∣
\cfrac{\triangledown f(x_0)}{|\triangledown f(x_0)|}
∣▽f(x0)∣▽f(x0)表示的是单位梯度，主要是方向(梯度的方向下降最猛)，有时候懒人就直接写
▽
f
(
x
0
)
\triangledown f(x_0)
▽f(x0)，方向前面乘上
λ
\lambda
λ就是步长，所以写成：
x
1
=
x
0
−
λ
▽
f
(
x
0
)
x_1=x_0-\lambda\triangledown f(x_0)
x1=x0−λ▽f(x0)。通项就是：
x
n
+
1
=
x
n
−
λ
▽
f
(
x
n
)
x_{n+1}=x_n-\lambda\triangledown f(x_n)
xn+1=xn−λ▽f(xn)
---------------------------------------------------------割你没商量1------------------------------------------------------
下面用数学的方法来估计一下步长
λ
\lambda
λ，记
f
(
x
n
+
1
)
=
f
(
x
n
−
λ
▽
f
(
x
n
)
)
=
g
(
λ
)
f(x_{n+1})=f(x_n-\lambda\triangledown f(x_n))=g(\lambda)
f(xn+1)=f(xn−λ▽f(xn))=g(λ)
这是一个关于
λ
\lambda
λ的函数，要使得步长小一些（如果步长太多就会无法到达最低点），就是要求函数的最小值，就是求导数并等于0：
g
′
(
λ
)
=
f
′
(
x
n
−
λ
▽
f
(
x
n
)
)
(
−
▽
f
(
x
n
)
)
=
0
g'(\lambda)=f'(x_n-\lambda\triangledown f(x_n))(-\triangledown f(x_n))=0
g′(λ)=f′(xn−λ▽f(xn))(−▽f(xn))=0
然后看如何解出
λ
\lambda
λ。
实际上
λ
\lambda
λ也不会取很大，一般是
1
0
−
3
∼
1
0
−
4
10^{-3}\sim10^{-4}
10−3∼10−4
---------------------------------------------------------割你没商量1------------------------------------------------------
对于整体的损失函数而言：
J
(
w
)
=
J
(
x
1
,
w
)
+
J
(
x
2
,
w
)
+
.
.
.
+
J
(
x
n
,
w
)
J(w)=J(x_1,w)+J(x_2,w)+...+J(x_n,w)
J(w)=J(x1,w)+J(x2,w)+...+J(xn,w)
如果n比较大，则每次计算梯度的时候都要把这些样本求和，再计算，运算很慢，所以有：
随机梯度下降
从
w
0
→
w
1
w_0\to w_1
w0→w1的梯度，只用第一个样本和输出
x
1
,
y
1
x_1,y_1
x1,y1来计算
J
(
x
1
,
w
)
J(x_1,w)
J(x1,w)
从
w
1
→
w
2
w_1\to w_2
w1→w2的梯度，只用第二个样本和输出
x
2
,
y
2
x_2,y_2
x2,y2来计算
J
(
x
2
,
w
)
J(x_2,w)
J(x2,w)
每一次只用一个样本来进行梯度计算虽然速度很快，但是会受到每一个样本的影响会很大，很容易被异常样本把结果带偏。因此出现了：
batch梯度下降
取batch size=100，
从
w
0
→
w
1
w_0\to w_1
w0→w1的梯度，使用
x
1
∼
x
100
x_1\sim x_{100}
x1∼x100来计算
J
(
w
)
=
{
J
(
x
1
,
y
1
,
w
)
J
(
x
2
,
y
2
,
w
)
⋮
J
(
x
100
,
y
100
,
w
)
J(w)=\begin{cases}J(x_1,y_1,w)\\J(x_2,y_2,w)\\\vdots\\J(x_{100},y_{100},w)\end{cases}
J(w)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧J(x1,y1,w)J(x2,y2,w)⋮J(x100,y100,w)
从
w
0
→
w
1
w_0\to w_1
w0→w1的梯度，使用
x
101
∼
x
200
x_{101}\sim x_{200}
x101∼x200来计算
J
(
w
)
=
{
J
(
x
101
,
y
101
,
w
)
J
(
x
102
,
y
102
,
w
)
⋮
J
(
x
200
,
y
200
,
w
)
J(w)=\begin{cases}J(x_{101},y_{101},w)\\J(x_{102},y_{102},w)\\\vdots\\J(x_{200},y_{200},w)\end{cases}
J(w)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧J(x101,y101,w)J(x102,y102,w)⋮J(x200,y200,w)
所有的样本都算完，就是已给epoch。
牛顿法（两种解释）
解释一
之前提过：求一个函数f(x)的最小值可以对函数f(x)求导并使其等于0(或者说使得梯度
▽
f
(
x
)
\triangledown f(x)
▽f(x)等于0)：
f
′
(
x
)
=
0
f'(x)=0
f′(x)=0
把函数f(x)的导数看做一个函数，令
g
(
x
)
=
f
′
(
x
)
⇒
g
(
x
)
=
0
g(x)=f'(x) \Rightarrow g(x)=0
g(x)=f′(x)⇒g(x)=0
用牛顿法求这个使得
g
(
x
)
=
0
g(x)=0
g(x)=0的过程也是已给迭代的过程
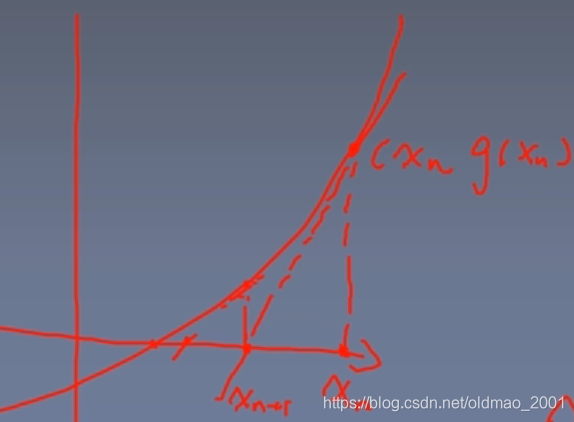
假设
g
(
x
)
g(x)
g(x)的函数曲线是这个样子，要找到那个
g
(
x
)
=
0
g(x)=0
g(x)=0的点，先做某个
x
n
x_n
xn的切线，然后找到切线与x轴相交的点
x
n
+
1
x_{n+1}
xn+1然后再做
x
n
+
1
x_{n+1}
xn+1的切线，以不断逼近
g
(
x
)
=
0
g(x)=0
g(x)=0的点。
先来求第一条切线的方程：
y
−
g
(
x
n
)
=
g
′
(
x
n
)
(
x
n
+
1
−
x
n
)
y-g(x_n)=g'(x_n)(x_{n+1}-x_n)
y−g(xn)=g′(xn)(xn+1−xn)
令y=0（就是上图中的
x
n
+
1
x_{n+1}
xn+1点）
−
g
(
x
n
)
=
g
′
(
x
n
)
(
x
n
+
1
−
x
n
)
x
n
+
1
−
x
n
=
−
g
(
x
n
)
g
′
(
x
n
)
x
n
+
1
=
x
n
−
g
(
x
n
)
g
′
(
x
n
)
-g(x_n) =g'(x_n)(x_{n+1}-x_n)\\ x_{n+1}-x_n =-\frac{g(x_n)}{g'(x_n)}\\ x_{n+1}=x_n-\frac{g(x_n)}{g'(x_n)}
−g(xn)=g′(xn)(xn+1−xn)xn+1−xn=−g′(xn)g(xn)xn+1=xn−g′(xn)g(xn)
再把
g
(
x
)
=
f
′
(
x
)
g(x)=f'(x)
g(x)=f′(x)带回来
x
n
+
1
=
x
n
−
f
′
(
x
n
)
f
′
′
(
x
n
)
x_{n+1}=x_n-\frac{f'(x_n)}{f''(x_n)}
xn+1=xn−f′′(xn)f′(xn)
这是二维的情况，如果是多维的情况：
x
n
+
1
=
x
n
−
H
−
1
▽
f
(
x
n
)
x_{n+1}=x_n-H^{-1}\triangledown f(x_n)
xn+1=xn−H−1▽f(xn)
其中H是海神矩阵，除以海神矩阵就是乘以它的逆矩阵。为什么这里是海神矩阵？因为
x
n
+
1
x_{n+1}
xn+1是
R
n
R^n
Rn的。
▽
f
(
x
n
)
\triangledown f(x_n)
▽f(xn)是n维向量，二次求导就是海神矩阵。
在机器学习中，要算海神矩阵的逆矩阵很麻烦，于是就引申出了很多种拟牛顿法BFGS（用另外一个矩阵来逼近海神矩阵的逆矩阵）。
解释二
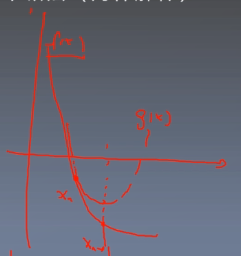
如上图所示，函数f(x)是一个复杂的曲线，然后在点
x
n
x_n
xn上用一个二次函数g(x)进行拟合,然后找到g(x)最低点
x
n
+
1
x_{n+1}
xn+1，然后把
x
n
+
1
x_{n+1}
xn+1代入f(x)继续拟合，不断迭代，直到取到f(x)的最小值，具体的计算过程如下：
先写出g(x)在
x
n
x_n
xn的泰勒展开，只用写到二次项：
g
(
x
)
=
f
(
x
n
)
+
f
′
(
x
n
)
(
x
−
x
n
)
+
f
′
′
(
x
n
)
2
(
x
−
x
n
)
2
+
.
.
.
g(x)=f(x_n)+f'(x_n)(x-x_n)+\frac{f''(x_n)}{2}(x-x_n)^2+...
g(x)=f(xn)+f′(xn)(x−xn)+2f′′(xn)(x−xn)2+...
g(x)是二次函数，可以写为
a
x
2
+
b
x
+
c
ax^2+bx+c
ax2+bx+c，那么最低点
x
n
+
1
x_{n+1}
xn+1可以看做最小值，根据初中的知识可以知道，最小值为：
x
=
b
2
a
x=\frac{b}{2a}
x=2ab
a是泰勒展开的二次项的系数，b是一次项的系数，把泰勒展开再展开，合并系数得：
a
=
f
′
′
(
x
n
)
2
a=\frac{f''(x_n)}{2}
a=2f′′(xn)
b
=
f
′
(
x
n
)
−
x
n
f
′
′
(
x
n
)
b=f'(x_n)-x_nf''(x_n)
b=f′(xn)−xnf′′(xn)
因此最低点
x
n
+
1
x_{n+1}
xn+1的值为：
x
n
+
1
=
−
f
′
(
x
n
)
−
x
n
f
′
′
(
x
n
)
f
′
′
(
x
n
)
=
x
n
−
f
′
(
x
n
)
f
′
′
(
x
n
)
(1)
x_{n+1}=-\frac{f'(x_n)-x_nf''(x_n)}{f''(x_n)}=x_n-\frac{f'(x_n)}{f''(x_n)}\tag{1}
xn+1=−f′′(xn)f′(xn)−xnf′′(xn)=xn−f′′(xn)f′(xn)(1)
这个和解释一推导出来的公式是一样的。
牛顿法要拟合，因此不能离最小值太远的地方拟合，要接近极小值再拟合收敛的效果越好。因此经常是先用梯度下降，到了局部极小值附近后再用牛顿法。
牛顿法收敛速度
按这个迭代原理，
x
0
x_{0}
x0就应该是函数的局部最优点，也就是
f
(
x
0
)
f(x_{0})
f(x0)有最小值，且有
f
′
(
x
0
)
=
0
f'(x_{0})=0
f′(x0)=0
要弄明白这个收敛速度，就是要比较下
x
n
+
1
x_{n+1}
xn+1到
x
0
x_{0}
x0的距离和
x
n
x_{n}
xn到
x
0
x_{0}
x0的距离的区别(把公式1代入下面)：
∣
x
n
+
1
−
x
0
∣
=
∣
x
n
−
f
′
(
x
n
)
f
′
′
(
x
n
)
−
x
0
∣
|x_{n+1}-x_{0}|=|x_{n}-\frac{f'(x_n)}{f''(x_n)}-x_{0}|
∣xn+1−x0∣=∣xn−f′′(xn)f′(xn)−x0∣
由于
f
′
(
x
0
)
=
0
f'(x_{0})=0
f′(x0)=0，所以分子加上
f
′
(
x
0
)
f'(x_{0})
f′(x0)不影响。
=
∣
x
n
−
f
′
(
x
n
)
−
f
′
(
x
0
)
f
′
′
(
x
n
)
−
x
0
∣
=|x_{n}-\frac{f'(x_n)-f'(x_{0})}{f''(x_n)}-x_{0}|
=∣xn−f′′(xn)f′(xn)−f′(x0)−x0∣
根据中值定理
f
(
b
)
−
f
(
a
)
=
(
b
−
a
)
f
′
(
ξ
)
,
a
<
ξ
<
b
f(b)-f(a)=(b-a)f'(\xi),a<\xi<b
f(b)−f(a)=(b−a)f′(ξ),a<ξ<b，分子有：
=
∣
x
n
−
(
x
n
−
x
0
)
f
′
′
(
ξ
)
f
′
′
(
x
n
)
−
x
0
∣
=\bigg|x_{n}-\frac{(x_n-x_{0})f''(\xi)}{f''(x_n)}-x_{0}\bigg|
=∣∣∣∣xn−f′′(xn)(xn−x0)f′′(ξ)−x0∣∣∣∣
=
∣
x
n
−
x
0
∣
∣
1
−
f
′
′
(
ξ
)
f
′
′
(
x
n
)
∣
=|x_n-x_{0}|\bigg|1-\frac{f''(\xi)}{f''(x_n)}\bigg|
=∣xn−x0∣∣∣∣∣1−f′′(xn)f′′(ξ)∣∣∣∣
=
∣
x
n
−
x
0
∣
∣
f
′
′
(
x
n
)
−
f
′
′
(
ξ
)
f
′
′
(
x
n
)
∣
=|x_n-x_{0}|\bigg|\frac{f''(x_n)-f''(\xi)}{f''(x_n)}\bigg|
=∣xn−x0∣∣∣∣∣f′′(xn)f′′(xn)−f′′(ξ)∣∣∣∣
再搞一次拉格朗日中值定理：
=
∣
x
n
−
x
0
∣
∣
(
x
n
−
ξ
)
f
′
′
′
(
η
)
f
′
′
(
x
n
)
∣
=|x_n-x_{0}|\bigg|\frac{(x_n-\xi)f'''(\eta)}{f''(x_n)}\bigg|
=∣xn−x0∣∣∣∣∣f′′(xn)(xn−ξ)f′′′(η)∣∣∣∣
令
∣
M
=
∣
f
′
′
′
(
η
)
f
′
′
(
x
n
)
∣
|M=\bigg|\cfrac{f'''(\eta)}{f''(x_n)}\bigg|
∣M=∣∣∣∣f′′(xn)f′′′(η)∣∣∣∣
=
∣
x
n
−
x
0
∣
∣
(
x
n
−
ξ
)
∣
M
=|x_n-x_{0}||(x_n-\xi)|M
=∣xn−x0∣∣(xn−ξ)∣M
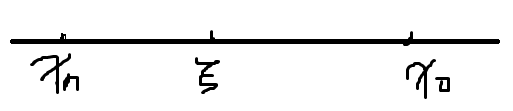
如上图所示，
ξ
\xi
ξ是在
x
n
∼
x
0
x_n\sim x_0
xn∼x0之间的，所以
∣
x
n
−
x
0
∣
∣
(
x
n
−
ξ
)
∣
M
<
(
x
n
−
x
0
)
2
M
|x_n-x_{0}||(x_n-\xi)|M<(x_n-x_{0})^2M
∣xn−x0∣∣(xn−ξ)∣M<(xn−x0)2M
由于M的分子分母都是导数，导数都是有界的，所以M是有界的，用
M
‾
\overline M
M表示其上界。
∣
x
n
−
x
0
∣
∣
(
x
n
−
ξ
)
∣
M
<
(
x
n
−
x
0
)
2
M
<
(
x
n
−
x
0
)
2
M
‾
|x_n-x_{0}||(x_n-\xi)|M<(x_n-x_{0})^2M<(x_n-x_{0})^2\overline M
∣xn−x0∣∣(xn−ξ)∣M<(xn−x0)2M<(xn−x0)2M
也就是：
∣
x
n
+
1
−
x
0
∣
<
(
x
n
−
x
0
)
2
M
‾
|x_{n+1}-x_{0}|<(x_n-x_{0})^2\overline M
∣xn+1−x0∣<(xn−x0)2M
当
x
n
和
x
0
x_n和x_{0}
xn和x0的距离小于1：
(
x
n
−
x
0
)
<
1
(x_n-x_{0})<1
(xn−x0)<1，则
(
x
n
−
x
0
)
2
<
<
1
(x_n-x_{0})^2<<1
(xn−x0)2<<1，说明是按照平方的速度进行收敛的，注意这里有条件：
x
n
和
x
0
x_n和x_{0}
xn和x0的距离小于1，如果距离大于1，上界会越来越大，没法收敛。
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
