判断链表是否有环以及寻找环入口

最新推荐文章于 2024-05-01 15:40:16 发布

原创最新推荐文章于 2024-05-01 15:40:16 发布 · 526 阅读

0 ·

CC 4.0 BY-SA版权

剑指offer 专栏收录该内容

39 篇文章

订阅专栏

本文介绍了一种使用快慢指针的方法来检测链表中是否存在环，并进一步找到环的入口节点。通过数学推导解释了为什么这种方法有效。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一. 判断是否有环

思路：采用“快慢指针”查检查链表是否含有环。让一个指针一次走一步，另一个一次走两步，如果链表中含有环，快的指针会再次和慢的指针相遇。

这里需要注意的一点是算法中循环的条件，这是一个很容易被忽略的细节。

1）因为fast指针比slow指针走得快，所以只要判断fast指针是否为空就好。由于fast指针一次走两步，fast.next可能已经为空（当fast为尾结点时），fast.next.next将会导致NullPointerException异常，所以在while循环中我们要判断fast.next是否为空；

2）考虑一个特殊情况，当输入的链表为空时，算法应该返回false，空链表肯定是不含有环的。如果没有fast != null，也会导致fast.next抛出NullPointerException异常。

代码：

public boolean hasCycle(ListNode head) {
        if(head == null){
            return false;
        }
        ListNode slow = head;
        ListNode fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
            if(slow == fast){
                return true;
            }
        }
        return false;
    }

二. 寻找环入口

第1题中判断出了链表是否有环，那么如果要寻找环的入口呢？

如下图所示：

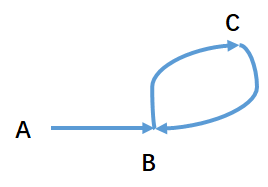
x表示头指针（A）到环的入口点（B）的距离

y表示环的入口点（B）到第一次相遇点（C)的距离

z表示第一次相遇点（C)到环的入口点（B）的距离。

假设慢指针走了s，那么快指针的速度是它的两倍，那么快指针走的路程为2s，所以有以下等式：

x+y=s

x+y+z+y=x+2y+z=2s

那么2(x+y)=x+2y+z，最终得出x=z。

也就是说，慢指针从头开始走，快指针继续往前走，它们的相遇点就是环的入口B。

如果没有环，返回空指针。

代码如下：

ListNode* EntryNodeOfLoop(ListNode* pHead)
{
    if (pHead == nullptr || pHead->next == nullptr) {
        return nullptr;
    }
    ListNode* slow = pHead;
    ListNode* fast = pHead;
    bool has_cycle = false;
    while (slow && fast && fast->next) {
        slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) {
          has_cycle = true;
          break;
        }
    }
    if (!has_cycle) {
        return nullptr;
    }
    slow = pHead;
    while (slow != fast) {
        slow = slow->next;
        fast = fast->next;
    }
    return slow;
}