--二叉树

基础知识

存储

#include<iostream>
#include<cstdio>
#include<queue>
using namespace std;//二叉树结点
struct node
{
    int data;//数据域
    node* lchild;//左子树
    node* rchild;//右子树
};

新建一个结点

node * newnode(int v)
{
    node * newn = new node;//申请一个node型变量
    newn->data = v;
    newn->lchild = newn->rchild = NULL;//初始状态下没有左右孩子
    return newn;//返回新建结点的地址
    }

查找并修改一个或多个

void search(node* root, int x, int newdata)
{
    if(root == NULL)
        return;//空树，死胡同(递归边界)
    if(root->data == x)//找到数据
        root->data = newdata;
                        //没有找到，往左右子树搜索x(递归式)
    search(root->lchild, x, newdata);
    search(root->rchild, x, newdata);
}

插入一个节点

//二叉树节点的插入位置就是数据域在二叉树中查找失败的位置
//注意根节点指针root要使用引用，否则插入不会成功(因为申请了变量)
void insert(node *&root, int x)
{
    if( root == NULL)//空树，说明查找失败，也就是要插入的位置（递归边界）
    {
        root = newnode(x);
        return;
    }
    else if (x<root->data) //由二叉树的性质，x应该插在左子树(这里是一颗搜索二叉树）
		insert(root->lchild, x);//往左子树搜索(递归式）
	else
        insert(root->rchild, x);//往右子树搜索（递归式）
}

创建二叉树

node* create(int data[], int n)
{
    node * root = NULL;//新建一个空根结点

    for(int i=0; i<n; i++)
        insert(root, data[i]);//将data[0]!data[n-1]插入二叉树中

    return root;//返回根节点
}

四种遍历

//二叉树的先序遍历
void preorder(node* root)//上左右（第一个为根结点）
{
    if(root == NULL)
        return;//到达空树，递归边界	
    printf("%d ", root->data);//访问根节点root，例如将其数据输出
    preorder(root->lchild);//访问左子树
    preorder(root->rchild);//访问右子树
}
//二叉树的中序遍历
void inorder(node* root)//左上右
{
    if(root == NULL)
        return;//到达空树，递归边界	
    inorder(root->lchild);//访问左子树    
    printf("%d ", root->data);//访问根节点root，例如将其数据输出
    inorder(root->rchild);//访问右子树
}
//二叉树的后序遍历
void postorder(node* root)//左右上（最后一个为根结点）
{
    if(root == NULL)
        return;//到达空树，递归边界	
    postorder(root->lchild);//访问左子树
    postorder(root->rchild);//访问右子树
    printf("%d ", root->data);//访问根节点root，例如将其数据输出
}
//二叉树的层次遍历(bfs)
void layerorder(node*root)
{
    if(root == NULL)
        return;//到达空树，递归边界	
    queue<node*> q;//注意队列里是纯地址
    q.push(root);//将根结点地址入队

    while(!q.empty())
    {
        node* now = q.front();//取出队首元素
        q.pop();
        printf("%d ", now->data);//访问队首元素
        if(now->lchild != NULL) q.push(now->lchild);
        if(now->rchild != NULL) q.push(now->rchild);
    }
}
int main()
{
    int a[] = {1,4,2,3,6};
    int n = 5;
    node * root = create(a, n);

    cout << "先序遍历：";
	preorder(root);//先序遍历
	cout << endl;

	cout << "中序遍历：";
	inorder(root);//中序遍历
	cout << endl;

	cout << "后序遍历：";
	postorder(root);//后序遍历
	cout << endl;

	cout << "层次遍历：";
	layerorder(root);//层次遍历
	cout << endl;

    return 0;
}
/* 
先序遍历：1 4 2 3 6 
中序遍历：1 2 3 4 6 
后序遍历：3 2 6 4 1 
层次遍历：1 4 2 6 3   */

利用遍历重建二叉树

//由先序遍历和中序遍历重建二叉树
//当前先序序列区间[preL,preR],中序序列区间为[inL,inR]，返回根结点地址
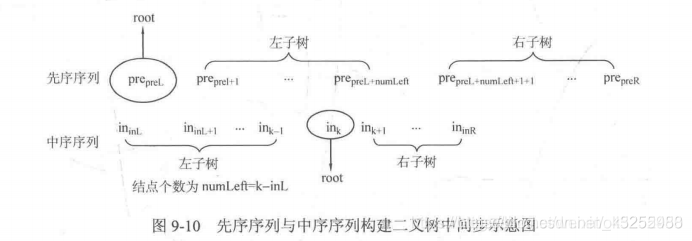
node * cre(int pre[], int prel, int prer, int in[], int inl, int inr)
{
    if(prel > prer)
        return NULL;//先序序列长度小于等于0时，直接返回
    node * root = new node;//新建一个节点，用来存放当前二叉树的根结点
    root->data = pre[prel];
    
    int k;
    for(k = inl; k<=inr;k++)
    {
        if(in[k] == pre[prel])//在中序序列中找到中结点
            break;
    }
    int numl = k - inl;//左子树的结点个数
    //左子树的先序区间为[prel+1,prel + numl],中序区间为[ inl, k - 1]
	//返回左子树的根节点地址，赋值给root的左指针
	root->lchild = cre(pre, prel + 1, prel + numl, in, inl, k - 1);

	//右子树的先序区间为[prel+numl+1,prer],中序区间为[k+1, inr]
	//返回右子树的根节点地址，赋值给root的左指针
	root->rchild = cre(pre, prel+numl+1, prer, in, k+1, inr);
	return root;
}

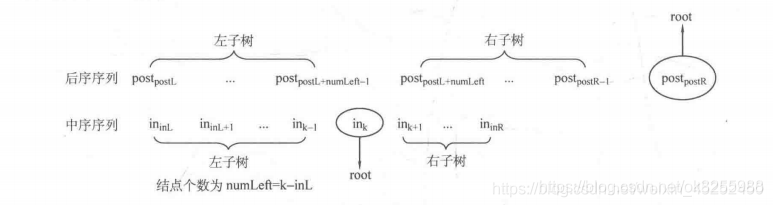
root->lchild = cre(post, postl, postl+ numl -1, in, inl, k - 1);
	root->rchild = cre(post, postl + numl, postr-1, in, k+1, inr);