Treap是一种结合了随机性的平衡搜索树，通过在节点中加入权重并维护最小堆属性来实现平衡。插入操作遵循二叉搜索树规则并随机赋予权值，通过左旋和右旋操作保持最小堆特性，确保树的平均高度较低。搜索操作则类似于二叉搜索树。题目提供了一种使用Treap解决操作查询问题的场景。
题目描述：
插入：向集合中添加一个数字k。
询问：询问集合中不超过k的最大数字。
题目要求对于每次询问，输出对应的答案。
解答：
本题可以用一个线性表来存储集合中的数字，对于每次询问，遍历一次线性表即可。但这样的思路对于每次询问都需要遍历整个线性表。对于集合元素较多并且查询操作较多时，效率很低。
比较好的思路是构建二叉搜索树，此时，对于每次查询，搜索的时间取决于当前状态下树的高度。但是对于某些情况，二叉搜索树会退化为一条线，此时的搜索效率也很低。这里介绍一种可以保证大多数情况下高度较低的平衡搜索树算法：
·Treap：
Treap一词取自“树(tree)”和“堆(Heap)”两个词的一部分，中文可译为：树堆。该数据结构结合了二叉搜索树和二叉堆的特征，树堆的节点定义如下：
节点中包含两个值：key 和 weight。其中key为关键字，意义和二叉搜索树中的关键字相同；weight则为节点的权值，树堆中节点的权值符合最小堆的特征，即父节点的权值一定比子节点的要小。下图是一个Treap的例子：
·插入和旋转：
在插入节点的过程中，节点根据二叉搜索树的插入规则进行插入，然后给节点随机赋予一个权值，此时新插入的节点的权值可能会破坏最小堆的特性，此时可以通过对树进行旋转，使其再次满足最小堆特性，而这个过程可以很好地平衡整个树的高度，使得在平均情况下，树的高度不会太高。旋转过程如下：
旋转分为左旋和右旋：左旋过程使得某节点的右孩子成为其父节点，右旋过程使得某节点的左孩子成为其父节点，过程如下：
左旋过程：将某节点的右孩子以该节点为轴向左旋转，使其成为该节点的父节点，同时该节点右孩子的左孩子成为该节点新的右孩子。如下图：
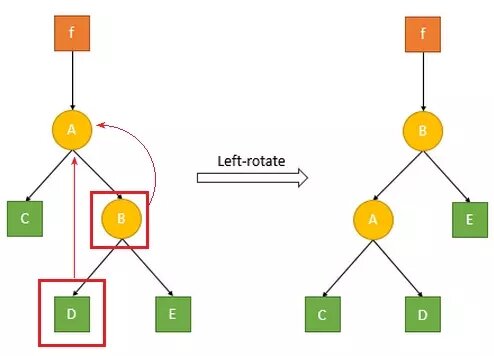
右旋的过程和左旋是对称的：将某节点的左孩子以该节点为轴向右旋转，成为该节点的父节点，同时该节点右孩子的左孩子成为该节点新的左孩子。如下图：
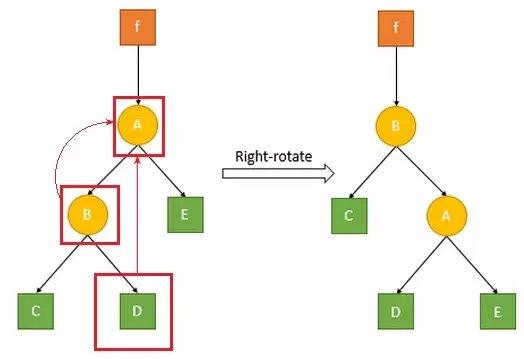
保持最小堆特性：
利用旋转的过程可以保持树中的最小堆特性，当新插入的节点的权值大小比其父节点还小时，利用旋转操作将其转化为当前父节点的父节点，然后在和其新的父节点比较权值，并执行相应的旋转操作就可以保证整个树恢复到最小堆特性。
旋转的过程会使得节点的左右子树的高度发生变化，这个过程可以将某一子树的高度减少同时将减少的高度添加到其兄弟节点的子树中。对于左右子树高度差异很大的情况，这个过程可以将其进行一定程度的缓解，从而使得整个树更加趋向于平衡。
搜索：
对于每次询问的过程，执行二叉搜索树的搜索过程即可。询问集合中不大于ｋ的最大数字，就在树中搜索数值k，过程如下：
① 从树的根节点开始搜索，对于每一轮搜索，执行步骤②，知道搜索到空节点。
② 对于某一轮搜索过程的当前搜索节点，如果该节点为空，则执行步骤③。否则，执行如下操作：如果该节点的key值比k小，则记录其key值，同时搜索其右孩子节点；如果当前key值比k大，则此时不记录，并搜索其左孩子节点。
③ 搜索过程搜索到了空节点，此时最后记录的key值就是要找的集合中不小于k的最大数值，算法结束。
备注：
本题也可以用红黑树来解答，该算法较为复杂。下文中的代码采用的是红黑树。
输入输出格式：
输入：第1行：1个正整数n，表示操作数量；第2..n+1行：每行1个字母c和1个整数k：若c为'I'，表示插入一个数字k到树中；若c为'Q'，表示询问树中不超过k的最大数字
输出：若干行：每行1个整数，表示针对询问的回答，保证一定有合法的解。
数据范围：
10≤n≤100,000
-1,000,000,000≤k≤1,000,000,000
程序代码：
/****************************************************/
/* File : Hiho_Week_103 */
/* Author : Zhang Yufei */
/* Date : 2016-06-25 */
/* Description : HihoCoder ACM program. (submit:g++)*/
/****************************************************/
#include<stdio.h>
#include<stdlib.h>
// Define the color of node.
#define RED 0
#define BLACK 1
/*
* Define the node of red-black tree.
* Parameters:
* @value: The value of node.
* @color: The color of node.
* @parent: The parent of this node.
* @left & @right: The left and right child of this node.
*/
typedef struct node {
int value;
int color;
struct node *parent;
struct node *left, *right;
} node;
// Define the null node.
node *nil;
// Define the RB-tree.
node *root = nil;
/*
* This function deals with the left rotate operation in tree.
* Parameters:
* @root: The root to operate.
* Returns:
* None.
*/
void left_rotate(node* current) {
node* right = current->right;
node* parent = current->parent;
node* right_left = right->left;
right->parent = current->parent;
if(current->parent != nil) {
if(current == current->parent->left) {
current->parent->left = right;
} else {
current->parent->right = right;
}
} else{
root = right;
}
current->parent = right;
right->left = current;
current->right = right_left;
right_left->parent = current;
}
/*
* This function deals with the right rotate operation in tree.
* Parameters:
* @root: The root to operate.
* Returns:
* None.
*/
void right_rotate(node* current) {
node* left = current->left;
node* parent = current->parent;
node* left_right = left->right;
left->parent = current->parent;
if(current->parent != nil) {
if(current == current->parent->left) {
current->parent->left = left;
} else {
current->parent->right = left;
}
} else {
root = left;
}
current->parent = left;
left->right = current;
current->left = left_right;
left_right->parent = current;
}
/*
* This function adjusts the tree to guarantee the attributes
* of RB_tree.
* Parameters:
* @node: The newly inserted node.
* Returns:
* None.
*/
void insert_fixup(node* ins) {
while(ins->parent->color == RED) {
node *p = ins->parent;
node *pp = ins->parent->parent;
if(p == pp->left) {
node *ppr = pp->right;
if(ppr->color == RED) {
ppr->color = BLACK;
pp->color = RED;
p->color = BLACK;
ins = pp;
} else if(ins == p->right) {
ins = p;
left_rotate(ins);
} else {
pp->color = RED;
p->color = BLACK;
right_rotate(pp);
}
} else {
node *ppl = pp->left;
if(ppl->color == RED) {
ppl->color = BLACK;
pp->color = RED;
p->color = BLACK;
ins = pp;
} else if(ins == p->left) {
ins = p;
right_rotate(ins);
} else {
pp->color = RED;
p->color = BLACK;
left_rotate(pp);
}
}
}
root->color = BLACK;
}
/*
* This function insert a node into RB_tree.
* Parameters:
* @The value to insert.
* Returns:
* None.
*/
void insert(int value) {
node *ins = (node*) malloc(sizeof(node));
ins->value = value;
ins->color = RED;
ins->left = ins->right = ins->parent = nil;
node *p = root;
node *pre = nil;
while(p != nil) {
pre = p;
if(p->value == value) {
free(ins);
return;
} else if(p->value > value) {
p = p->left;
} else {
p = p->right;
}
}
if(root == nil) {
root = ins;
} else {
if(pre->value > value) {
pre->left = ins;
} else {
pre->right = ins;
}
ins->parent = pre;
}
insert_fixup(ins);
}
/*
* This function search the answer for each query.
* Parameters:
* @value: The range value.
* Returns:
* The answer of the search.
*/
int search(int value) {
node *p = root;
int max = -1000000001;
while(p != nil) {
if(p->value > value) {
p = p->left;
} else {
if(max < p->value) {
max = p->value;
}
p = p->right;
}
}
return max;
}
void print(node* root) {
if(root == nil) {
printf("nil");
} else {
printf("(%d: ", root->value);
print(root->left);
printf(", ");
print(root->right);
printf(")");
}
}
/*
* The main program.
*/
int main(void) {
nil = (node*) malloc(sizeof(node));
nil->value = -1;
nil->color = BLACK;
nil->left = nil->right = nil->parent = NULL;
root = nil;
int n;
scanf("%d", &n);
for(int i = 0; i < n; i++) {
char c;
int k;
getchar();
scanf("%c %d", &c, &k);
if(c == 'I') {
insert(k);
} else if(c == 'Q') {
printf("%d\n", search(k));
}
//print(root);
// printf("\n");
}
return 0;
}
扫一扫
4595
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
