【自用】图像压缩感知（一）

最新推荐文章于 2025-05-20 15:27:42 发布

o__O_pyx

最新推荐文章于 2025-05-20 15:27:42 发布

阅读量4.9k

点赞数 4

CC 4.0 BY-SA版权

分类专栏：数字图像处理笔记

本文链接：https://blog.youkuaiyun.com/o__O_pyx/article/details/104149190

数字图像处理同时被 2 个专栏收录

9 篇文章

订阅专栏

笔记

9 篇文章

订阅专栏

本文探讨了层析成像中无条纹图像重建的关键技术，包括满足Shannon/Nyquist准则的视角采样，以及如何使用压缩感知理论进行欠采样投影的精确图像重建。介绍了压缩感知理论的基本原理，包括稀疏变换、信号重构和有限等距性质(RIP)。阐述了CT图像重建中的压缩感知应用，以及如何通过迭代算法如ART实现欠采样数据的重建。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

为了在层析成像中重建无条纹图像，视角的采样必须满足Shannon/Nyquist准则。当视角数小于Shannon/Nyquist限制时，重建图像中会出现视图混叠伪影。
已经证明，如果样本是随机分布的，则可以使用高度欠采样的投影精确地重建稀疏图像。

1 压缩感知理论
- 稀疏变换
- 信号重构
2 压缩感知理论框架下的CT图像重建
- 重建目标
- 具体表示
3 迭代类算法
- ART算法

1 压缩感知理论

A s.t. B 在约束条件B下求解A

稀疏变换

CS理论框架
x代表长度为N的一维K稀疏离散时间信号，Phi为N*N的稀疏基，β是N1维的稀疏列向量。

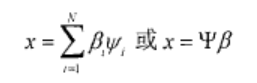
时域信号x可以用Phi变换域中的信号Beta等价表示。
用一个**MN**(M<<N)的变换矩阵Φ对信号进行线性投影，得到M*1的线性测量向量y：
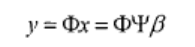
在这里插入图片描述
对于K稀疏信号x，上式中的Φ需要满足有限等距性质（Restricted Isometry Property, RIP），则K个系数就能够从M个测量值准确重构（得到一个最优解）。
RIP等价于测量矩阵Φ和稀疏基Ψ不相关。

信号重构

压缩感知理论将信号x的重构转化为有约束的L0范数最小化问题：
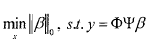
在这里插入图片描述
其中β的L0范数 ||β||₀ 表示向量中非零值的数量。
但是，L0范数最优化问题的数值不稳定，而且是NP非凸优化问题。
通常将L0范数最优化问题转换成L1范数最优化问题，凸优化问题：

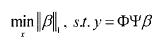
其中β的L1范数 ||β||₁ 表示图像像素值的绝对值之和：
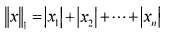
在这里插入图片描述
可以使用优化算法从这些投影中重建信号。

2 压缩感知理论框架下的CT图像重建

重建目标

压缩感知理论框架下的图像重建问题也可以转化为有线性约束的最小化问题：
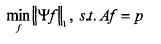
在这里插入图片描述
其中，f为待求的未知图像阵列，Ψ为某种稀疏变换（使图像f经变换后是稀疏的），A为M*N的系统矩阵，且M<<N，p为投影数据。
对于某些成像问题,通过对图像函数施加一个强假设,可以得到稀疏投影数据的较精确的迭代重建方案。例如,在血管的欠采样投影数据重建时,可以假设三维血管结构是稀疏的。可以设计一种有效的迭代算法，从稀疏投影数据中寻找最优解。大致过程为：
通过在图像f生成测量投影数据p这一事实的约束下，最小化图像的L1范数来实现。L1范数最小化受到线性约束，最终得到稀疏解。[29,30]

通常在医学和其他应用中,断层图像在一定体积内相对恒定，例如在器官内。图像的快速变化可能只发生在内部结构的边界处。因此,图像本身可能不是稀疏的，但是通过取其梯度的大小形成的图像可能近似稀疏[17],如图所示。离散梯度变换(DGT)也是目前图像迭代重建中广泛应用的稀疏约束[31-34]。

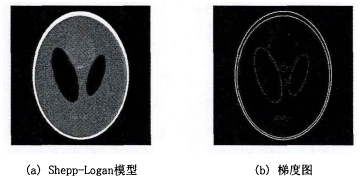
在这里插入图片描述
利用Shepp-Logan模型演示了图像梯度的稀疏特性。如果像素值由f_i,j标记，则图像梯度幅值为：

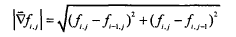
利用梯度变换代替下式中的稀疏变换Ψ：

最小化问题的目标函数为图像梯度幅值的L1范数，也就是图像的全变差(TV)，也称为图像的TV范数：
在这里插入图片描述

综上所述，压缩感知框架下的重建模型可转化为有约束的TV最小化问题。
在这里插入图片描述
如何求解？见图像压缩感知（二）

具体表示

图像函数表示为N_image的离散向量f，其中各个元素为：f_s(s=1,2,…,N_image)。当需要在二维图像中索引像素时，可以使用双下标形式f_i,j：
在这里插入图片描述
其中，整数H和W分别表示二维图像的高度和宽度，像素总数N_image=W×H。
投影数据向量表示为长度为N_data的离散向量p，其中各个测量值为：p_t（t=1,2,…,N_data）。

ART/EM等传统的CT迭代图像重建技术被用作求解线性系统Af=p的一些普通数值计算方法，即在TV算法中仅用于提供满足数据约束Af=p的图像f。
根据压缩感知算法对图像函数施加的约束条件、需要最小化的成本函数以及迭代方案的不同，来区分不同的算法。

3 迭代类算法

将图像重建问题转化为一个多维欠定方程组求解问题，主导思想是首先根据图像的性质建立一个目标函数，然后在满足己知的约束条件下使目标函数最优化。
代数重建技术(ART)[13,27]和期望最大化(EM)算法[13,14]是两种广泛使用的迭代类断层重建算法。

ART算法

在二维图像重建中，对于一个有W个像素的重建阵列，以及有M条射线穿过图像，ART算法实质上就是对的方程组求解，将矩阵展开为：
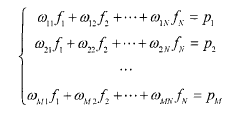
在这里插入图片描述
其中，f_n表示图像阵列中第n个位置的像素值，p_m个第条射线上的投影值，ω_mn表示第n个像素对第m条射线的贡献率，所有ω_mn组成一个MxN的矩阵W，即为系统矩阵。

通常在稀疏投影数据的重建中方程组是欠定的。ART算法就是通过迭代寻找能够满足一定收敛条件的{f₁,f₂,…,f_N}组合。首先将图像矩阵初始化，然后按照Kaczmarz迭代法执行如下迭代过程：对前一次迭代的结果图像相对于第m条射线进行正投影，获得第w条射线的投影值
将原始投影数据与步骤(1)中获得的投影数据作差，计算误差
对投影数据的差值作反投影，得到一个图像修正矩阵
使用步骤(2)得到的修正矩阵，对上次的图像估计中的像素值进行更新，得到新的图像估计
将步骤(4)得到的图像估计作为下一条射线迭代的输入，重复步骤(1)、(2)、(3)，直至m=M
检验是否满足收敛条件或符合迭代停止条件，否则将得到的图像估计作为输入，重复步骤(1)、(2)、(3)、(4)，直至满足条件，输出重建图像矩阵

对于第m条射线的第k次迭代过程，重建图像序列上第j个像素的更新公式为：
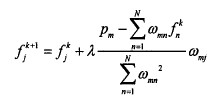
在这里插入图片描述
其中，λ为松弛因子，用来控制收敛速度，通常0<λ<2。