用最少的箭引爆气球----leetcode--贪心

最新推荐文章于 2021-09-25 18:37:31 发布

原创最新推荐文章于 2021-09-25 18:37:31 发布 · 365 阅读

0 ·

CC 4.0 BY-SA版权

java 同时被 2 个专栏收录

140 篇文章

订阅专栏

leetcode

37 篇文章

订阅专栏

本文探讨了一个二维空间中，通过精确计算找出引爆所有气球所需最少箭数的算法问题。介绍了解法1，不进行排序，逐个寻找可引爆多个气球的最佳射击点；解法2，先对气球坐标按结束点排序，再逐个射击，避免重复覆盖。两种方法均旨在减少射击次数，实现最优解。

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以y坐标并不重要，因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。

一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend，且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

Example:

输入:
[[10,16], [2,8], [1,6], [7,12]]

输出:
2

解释:
对于该样例，我们可以在x = 6（射爆[2,8],[1,6]两个气球）和 x = 11（射爆另外两个气球）。

解法1，不对数组进行排序，每次都要进行比较

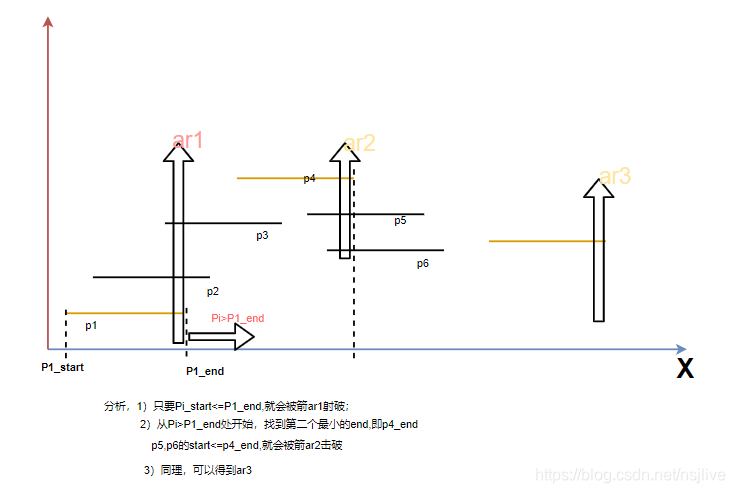
分析：1）找到end最小值对应的气球，标注为P1，在P1_end处射爆气球，则所有与P1交集的气球都可以被射爆（如下图ar1)；

问题：哪些气球Pi与P1有交集呢？ 只要求Pi_start<=P1_end即可；(如下图中的p2,p3的start都小于P1_end)

for(i=0;i<len;i++) {
if(points[i][0]>start&&points[i][1]<=end) {
k=i;
end=points[i][1];//找到end最小值
}
}

2）现在只需要考虑start>P1_end的气球即可；寻找到这样一个气球，标注为P2,（P2肯定与P1没有交集），在P2_end处射爆气球，则所有与P2有交集但是与P1没有交集的气球都可以被射爆；

start=points[k][1];

3）类推，找到气球P3,要求P3_start>P2_end,...

代码：

public class Solution {
    public static void main(String[] args) {
        int[] [] arr={{10,16},{2,8},{1,6},{7,12}};
        Solution test=new Solution();
        System.out.println(test.findMinArrowShots(arr));
    }
    public int findMinArrowShots(int[][] points) {
        int i,len=points.length,ans=0,k=0,end;
        double start=-2147483649.0;
        boolean added[]=new boolean[len],flag=true;
        while(flag) {
            flag=false;
            end=Integer.MAX_VALUE;

//每次找出一个新的end值最小的气球，在end端击破
            for(i=0;i<len;i++) {
                if(!added[i]&&(double)(points[i][0])>start&&points[i][1]<=end) {
                    k=i;
                    end=points[i][1];
                    flag=true;
                }
            }
            if(flag) {
                added[k]=true;
                start=points[k][1];
                ans++;//箭的数字加一
            }
        }
        return ans;
    }
}

参考：

https://blog.youkuaiyun.com/cobracanary/article/details/88873785

https://blog.youkuaiyun.com/weixin_31866177/article/details/87949657

解法2，对数组按照第二个元素进行排序

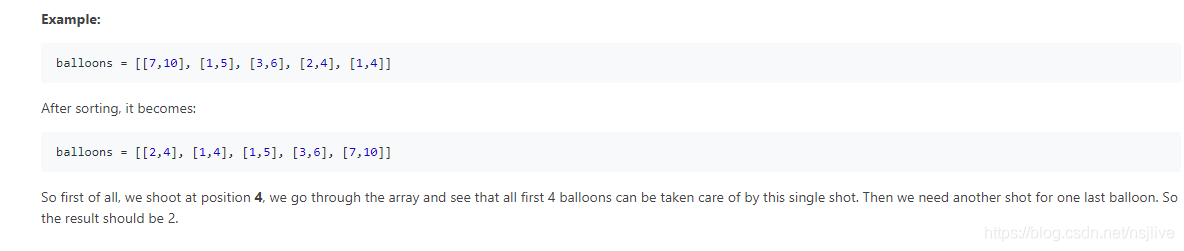
参考：https://leetcode.com/problems/minimum-number-of-arrows-to-burst-balloons/discuss/93703/Share-my-explained-Greedy-solution

所以首先，我们在第4位进行射击，我们通过阵列看到所有前4个气球都可以通过这一次射击得到照顾。然后我们需要另一个射击最后一个气球。所以结果应该是2。

/**
 * lambda数组排序
 * 对二维数组里面的元素（子数组）进行排序
 * 例如：a,b 子数组也是相当于{10,16},{2,8}
 * a[0]=10,a[1]=16,用a[1]-b[1]相当于按照子数组中的第二个元素进行升序排序；
 * b[1]-a[1]相当于按照子数组中的第二个元素进行降序排序；
 */

Arrays.sort(points, (a, b) -> a[1] - b[1]);//lambda数组正序排序

public int findMinArrowShots(int[][] points) {
        if (points.length == 0) {
            return 0;
        }
        /**
         * lambda数组排序
         * 对二维数组里面的元素（子数组）进行排序
         * 例如：a,b 子数组也是相当于{10,16},{2,8}
         * a[0]=10,a[1]=16,用a[1]-b[1]相当于按照子数组中的第二个元素进行升序排序；
         * b[1]-a[1]相当于按照子数组中的第二个元素进行降序排序；
         */
        Arrays.sort(points, (a, b) -> a[1] - b[1]);//lambda数组正序排序
        int arrowPos = points[0][1];
        int arrowCnt = 1;
        for (int i = 1; i < points.length; i++) {
            if (arrowPos >= points[i][0]) {
                continue;//终止本次循环，接着还执行后面的循环
            }
            arrowCnt++;
            arrowPos = points[i][1];
        }
        return arrowCnt;
    }