数和二叉树基本概念与性质

数和二叉树基本概念与性质

一、树的基本概念

1、树的定义

树(Tree)是n个结点的有限集合T，若n=0时称为空树。其中，最顶层的结点，称之为根节点。根结点可以有任意数量的子结点，每个子结点也可以有任意数量的子结点。

2、树的基本术语

（1）结点（node）

一个数据元素及若干指向其子树的分支。如上图中，A, B, C … 均为结点，结点A为根结点

（2）结点的度（degree）

结点所拥有的子树的棵树称为结点的度。如上图中，结点A的度是3，结点B的度是2，结点K的度是0

（3）树的度

树中结点度的最大值成为树的度。如上图中，树的度是3

（4）叶子结点、非叶子结点

树中度为0的结点成为叶子结点（终端结点）。上图中结点 F, H, I, J, K, L, M, N均为叶子结点
度不为0的结点称为非叶子结点（非终端结点或分支结点）
除根结点以外，分支结点又称为内部结点

（5）孩子结点、双亲结点、兄弟结点

如上图中
结点B，C，D是结点A的子结点（孩子结点），结点A是结点B，C，D的父结点
结点E，F 是结点B的子结点，结点B是结点E，F的父结点
结点B，C，D为兄弟结点

（6）结点的层次路径、祖先、子孙

从根结点开始，到达某结点P所经过的所有节点形成结点P的层次路径，某结点的层次路径有且只有一条。如上图所示，结点K的层次路径为A-B-E-K
结点P的层次路径上所有结点（P除外）称为P的祖先。如上图所示，A，B，E均为K的祖先
以某一结点为根的子树中的任意结点称为该结点的子孙节点。如上图所示，K，L为结点E的子孙结点。

（7）树的深度（depth）

树中结点的最大层次值，又称为树的高度。如上图所示，书的深度为4。可以理解为一共有多少代。

（8）有序树和无序树

对于一棵树，若其中每一个结点的子树具有一定的次序，则该树为有序树，否则称为无序树。
详细讲解见相关链接：链接: 有序树和无序树的区别.

（9）森林

有多棵互不相交的树的集合。

二、二叉树

1.二叉树的定义

二叉树（Binary tree）是n（n>0）个结点的有限集合。
（1）有且只有一个根结点
（2）其余的结点被分为两个互不相交的子集，分别称为左子树、右子树，并且左子树和右子树都是二叉树
（3）二叉树是有序树

2.二叉树的基本形态

二叉树有5种基本形态，如图所示

对于n个结点的二叉树，其形态总数为
$$\frac{C_{2n}^n}{n+1}$$

3.二叉树的分类

3.1 满二叉树

一个深度为k，且有$2^k-1$个结点的二叉树称为满二叉树。

满二叉树编号按“自上而下，自左至右”原则进行

3.2 完全二叉树

如果深度为k，有n个结点的二叉树，当且仅当其每一个结点都与深度为k的满二叉树中编号从1到n的结点一一对应，该二叉树称为完全二叉树。

4.二叉树的性质

性质1：
在非空二叉树中，第i层上有$2^{i-1}$个结点。

首项为1，公比为2的等比数列，第n项为$2^{n-1}$

性质2：
深度为k的二叉树至多有$2^i-1$个结点。

首项为1，公比为2，前n项和为$2^n-1$

性质3：
对任何一棵二叉树，若其叶子结点数为$n_0$，度为2的结点数为$n_2$，则$n_0=n_2+1$

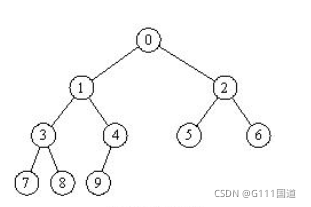
证明：
设二叉树的总结点数为N，叶子结点数为$n_0$，度为1的结点数为$n_1$，度为2的结点数为$n_2$，则有$$N=n_0+n_1+n_2$$
除根结点外，其余每一个结点都有唯一的一个进入分支，而所有的分支都是由度为1和2的结点射出的。设二叉树分支总数为B，则有$$B=n_1+2n_2$$同时$$N=B+1$$二者联立$$n_0+n_1+n_2=n_1+2n_2+1$$求得$$n_0=n_2+1$$

推广：
对于m度数，$n_i$表示度为i的结点个数，则有：$$n_0=n_2+2n_3+3n_4+4n_5+...+（m-1）n_m+1$$

5.完全二叉树的性质

性质1：
完全二叉树中，第i层上有$2^{i-1}$个结点。

首项为1，公比为2的等比数列，第n项为$2^{n-1}$

性质2：
深度为k的完全二叉树至多有$2^i-1$个结点。

首项为1，公比为2，前n项和为$2^n-1$

性质3：
对任何一棵完全二叉树，若其叶子结点数为$n_0$，度为2的结点数为$n_2$，则$n_0=n_2+1$

性质4：
深度为k的满二叉树中，编号从1到n的前n个结点构成了一棵深度为k的完全二叉树。其中$2^{k-1}\le n\le 2^k-1$

性质5：
若完全二叉树深度为k，则所有的叶子结点都出现在第k层或者k-1层。
性质6：
对于任意一个完全二叉树，如果其右子树的最大层次为K，则其左子树的最大层次为K或K+1。
性质7：
对于n个结点的完全二叉树，其深度为$[lo{g}_{2}n]+1$。

其中，$[x]$表示不大于x的最大整数
该性质可由性质4推导证明

性质8：
对于一棵有n个结点的完全二叉树，其结点按照层序自左向右进行编号，且根结点编号为1，则对于编号为i的结点：
（1）若i=1，则结点i是二叉树的根，无双亲结点；当i>1，则其双亲结点编号为$[i/2]$
（2）如果2i>n，则结点i为叶子节点，无左孩子；否则，其左孩子结点编号为2i
（3）如果2i+1>n，则结点i无右孩子，否则，其右孩子结点编号为2i+1