Libre OJ #6279 数列分块入门 3

最新推荐文章于 2021-11-08 09:41:46 发布

Error Man

最新推荐文章于 2021-11-08 09:41:46 发布

阅读量206

点赞数 1

CC 4.0 BY-SA版权

分类专栏： # 分块、莫队

本文链接：https://blog.youkuaiyun.com/no_O_ac/article/details/98475599

分块、莫队专栏收录该内容

10 篇文章

订阅专栏

本文介绍了一种基于数列分块的优化算法，通过预处理将数组分为多个块，每个块内部进行排序并标记更新操作，以加速区间查询和更新的效率。详细解释了算法的实现过程，包括构建块、更新和查询操作的具体步骤。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

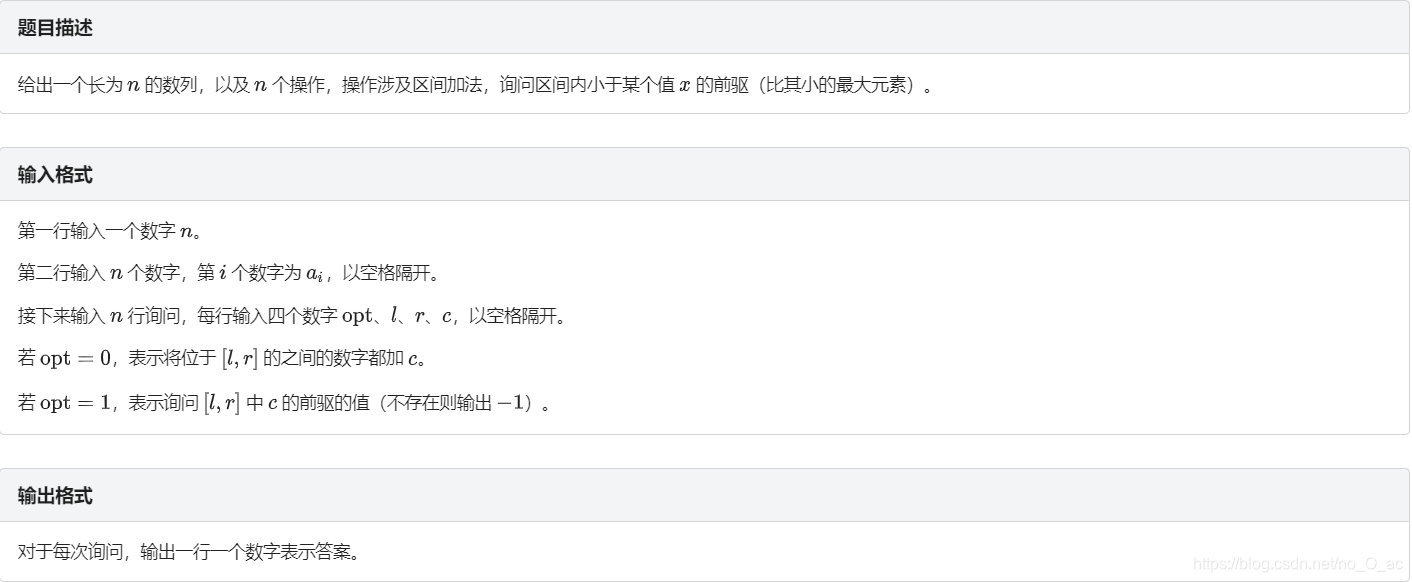
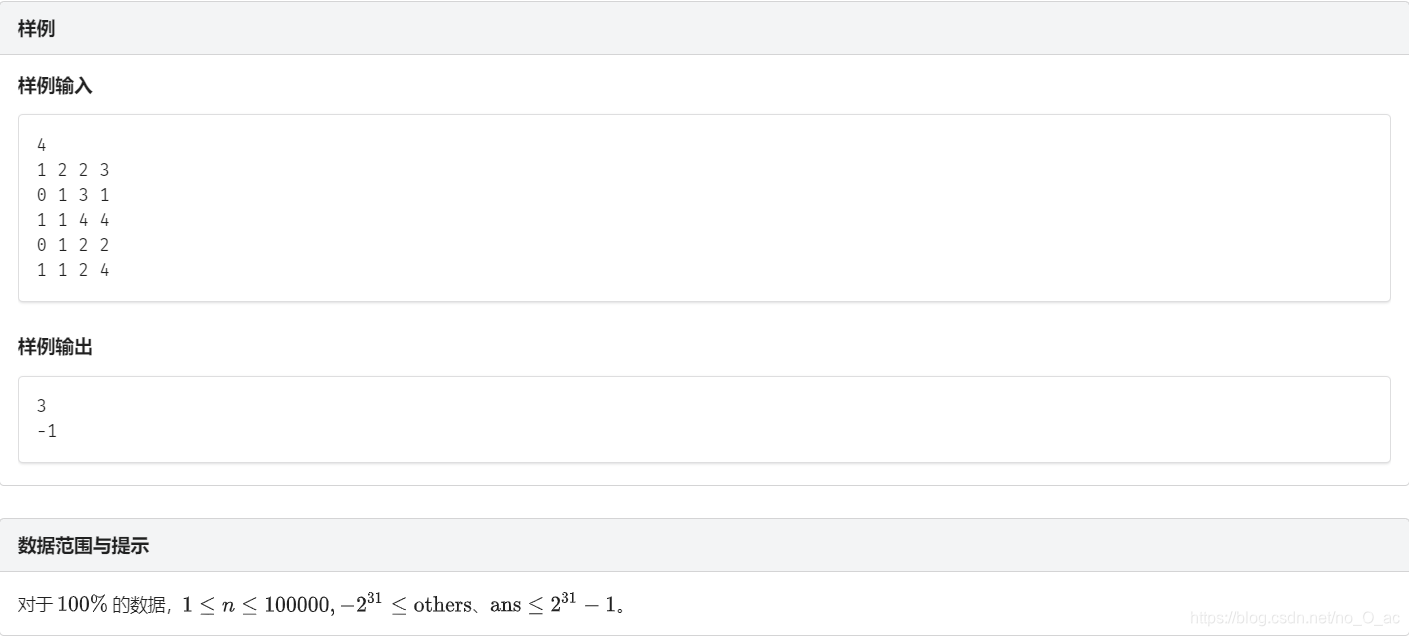
思路：和数列分块2几乎一样，在 lower_bound 处理答案时有点区别。

Code：

#include<bits/stdc++.h>
#define debug(x) cout << "[" << #x <<": " << (x) <<"]"<< endl
#define pii pair<int,int>
#define clr(a,b) memset((a),b,sizeof(a))
#define rep(i,a,b) for(int i = a;i < b;i ++)
#define pb push_back
#define MP make_pair
#define LL long long
#define ull unsigned LL
#define ls i << 1
#define rs (i << 1) + 1
#define fi first
#define se second
#define CLR(a) while(!(a).empty()) a.pop()

using namespace std;

const int maxn = 1e5 + 10;
const int inf = 0x3f3f3f3f;
int block,num,n;
int a[maxn],b[maxn],tag[maxn];
int l[maxn],r[maxn],belong[maxn];

void build(){
    block = sqrt(n);
    num = n / block; if(n % block) ++ num;
    for(int i = 1;i <= num;++ i){
        l[i] = (i - 1) * block + 1;
        r[i] = i * block;
    }
    r[num] = n;
    for(int i = 1;i <= n;++ i)
        belong[i] = (i - 1) / block + 1;
}

void Resort(int id){
    int x = l[id],y = r[id];
    for(int i = x;i <= y;++ i){
        a[i] += tag[id];
        b[i] = a[i];
    }
    sort(b + x,b + y + 1);
    tag[id] = 0;
}

void update(int x,int y,int c){
    if(belong[x] == belong[y]){
        for(int i = x;i <= y;++ i)
            a[i] += c;
        Resort(belong[x]);
        return ;
    }
    for(int i = x;i <= r[belong[x]];++ i)
        a[i] += c;
    Resort(belong[x]);
    for(int i = belong[x] + 1;i < belong[y];++ i)
        tag[i] += c;
    for(int i = l[belong[y]];i <= y;++ i)
        a[i] += c;
    Resort(belong[y]);
}

int query(int x,int y,int c){
    int ans = -inf;
    if(belong[x] == belong[y]){
        for(int i = x;i <= y;++ i)
            if(a[i] + tag[belong[x]] < c)
                ans = max(ans,a[i] + tag[belong[x]]);
        return ans;
    }
    for(int i = x;i <= r[belong[x]];++ i)
        if(a[i] + tag[belong[x]] < c)
            ans = max(ans,a[i] + tag[belong[x]]);
    for(int i = belong[x] + 1;i < belong[y];++ i){
        int pos = lower_bound(b + l[i],b + r[i] + 1,c - tag[i]) - b;
        if(b[pos - 1] + tag[belong[pos - 1]] < c)
            ans = max(ans,b[pos - 1] + tag[belong[pos - 1]]);
    }
    for(int i = l[belong[y]];i <= y;++ i)
        if(a[i] + tag[belong[y]] < c)
            ans = max(ans,a[i] + tag[belong[y]]);
    return ans;
}

int main() {
#ifndef ONLINE_JUDGE
    freopen("in.txt", "r", stdin);
    freopen("out.txt", "w", stdout);
#endif
    scanf("%d",&n);
    for(int i = 1;i <= n;++ i)
        scanf("%d",&a[i]);
    b[0] = inf;
    build();
    for(int i = 1;i <= num;++ i) Resort(i);
    while(n --){
        int op,x,y,c; scanf("%d%d%d%d",&op,&x,&y,&c);
        if(!op)
            update(x,y,c);
        else{
            int ans = query(x,y,c);
            printf("%d\n",ans == -inf ? -1 : ans);
        }
    }
    return 0;
}