计算机视觉技术驱动下的智能油藏建模与数据同化方法体系研究

原创于 2025-12-10 21:48:52 发布 · 817 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#计算机视觉 #人工智能

『AI先锋杯·14天征文挑战第9期』 5w人浏览 52人参与

1 引言

现代石油工程领域正经历着由数据驱动的技术变革，传统依赖人工解释与经验统计的油藏表征方法在应对深层-超深层、非常规等复杂油气藏时显现出显著的局限性。油藏建模作为油气开发决策的核心环节，其精度直接决定了采收率预测、井位优化及经济风险评估的可靠性。然而，地下储层固有的地质复杂性、强非均质性以及数据获取的高成本特性，导致现有技术体系面临三大根本性挑战：其一，地震、测井、岩心等多源数据在空间尺度与分辨率上存在数量级差异，跨尺度信息融合缺乏有效机制；其二，人工解释过程引入的主观偏差与效率瓶颈制约了模型更新频率；其三，基于物理方程的数值模拟虽然机理完善，但高昂的计算成本使其难以满足实时决策需求。近年来，以深度学习为代表的计算机视觉技术在医学影像、自动驾驶等领域的突破，为解决上述难题提供了跨学科的技术范式迁移可能[4]。该技术体系通过卷积神经网络、生成对抗网络、扩散模型等算法架构，能够实现从微观孔隙结构到宏观地震体的多尺度图像自动解译，将主观解释转化为可重复的定量分析流程。特别值得注意的是，数据同化作为连接静态地质模型与动态生产数据的桥梁，其与计算机视觉的深度融合催生了新一代智能油藏管理框架，使得在不确定性量化基础上实现模型自动更新成为可能。本文系统阐述计算机视觉在油藏建模全链条中的理论方法、技术实现路径及现存挑战，重点剖析特征提取、代理建模、实时监测等关键环节的技术内涵，为构建可扩展、可解释、物理自洽的智能化油藏工作流提供理论支撑。

2 油藏建模与数据同化的理论技术基础

2.1 油藏建模基础理论框架解析

油藏建模的本质是通过整合多尺度、多类型数据构建能够反映地下真实情况的数字孪生体，其理论基础涵盖地质统计学、岩石物理学与渗流力学三大支柱。在地质框架构建阶段，构造型建模依赖地震解释成果确定断层与层位空间关系，沉积相建模则通过变差函数分析表征相带分布规律[2]。传统方法采用基于目标的示性点过程或基于象元的序贯指示模拟，这些方法虽能保证空间变差结构，但在处理多变量非线性关系时存在固有缺陷。岩石物理建模环节，孔隙度-渗透率关系通常通过岩心刻度建立经验公式，然而此类统计模型难以捕捉成岩作用、裂缝发育等因素导致的局部偏离。更为关键的是，三维地质模型向数值模拟器的转换过程中，网格粗化引起的尺度升级效应会导致关键渗流通道信息丢失，传统渗透率升级方法如简单平均、数值试井等无法系统保留空间连通性特征[10]。动态模拟过程求解多相渗流控制方程时，相对渗透率曲线与毛管压力函数的参数不确定性会随时间累积，最终导致历史拟合收敛困难。现代油藏建模理论正从确定性框架转向概率性描述，将模型参数视为随机变量，通过贝叶斯理论构建后验分布，这为数据同化技术的引入奠定了数学基础[1]。

2.2 数据同化技术体系演进

数据同化旨在通过观测数据动态更新模型参数以减小预测不确定性，其理论发展经历了从线性到非线性、从确定性到概率性的演进路径。集合卡尔曼滤波（EnKF）作为里程碑式算法，通过蒙特卡洛采样传播不确定性，避免了计算复杂的梯度矩阵，在实时生产优化中广泛应用[5]。其核心思想是利用观测数据对状态向量进行卡尔曼增益校正，但线性高斯假设在强非线性油藏系统中会导致滤波发散。为此发展的集合平滑多数据同化（ES-MDA）通过多次迭代平滑过程改善非线性处理能力，却仍受限于集合规模与协方差矩阵秩亏问题[18]。贝叶斯反演框架提供了更严格的概率诠释，将模型更新转化为后验采样问题，马尔可夫链蒙特卡洛（MCMC）方法虽能精确刻画后验分布，但海量正演模拟使其在三维大尺度模型中难以实用[19]。变分同化方法通过构造代价函数最小化观测与模拟差异，伴随状态法计算梯度效率较高，但伴随代码开发维护成本巨大。近年来，机器学习被用于构建快速代理模型替代数值模拟器，显著降低单次同化计算成本，但代理模型本身的近似误差会引入新的不确定性源。数据同化与计算机视觉的结合点在于，图像数据可作为软约束进入同化系统，例如地震振幅变化约束饱和度场更新、微CT孔隙结构约束渗透率分布，这种多源异构数据融合显著提升了参数估计的稳定性。

2.3 计算机视觉在地球科学中的技术谱系

计算机视觉技术体系在地球科学领域的应用经历了由传统图像处理向深度表示学习的范式转变[15]。早期基于形态学操作、边缘检测算子的方法依赖人工设计特征，对噪声敏感且泛化能力差。2012年后，深度卷积神经网络（CNN）通过层级化特征自动学习彻底改变了这一格局[3]。在地球科学图像分析中，U-Net架构因其编码-解码结构与跳跃连接设计成为分割任务的事实标准，能够有效融合多尺度上下文信息[8]。残差网络（ResNet）通过恒等映射缓解梯度消失，使训练百层以上网络成为可能，在地震相识别中展现出优异的特征抽象能力。Vision Transformer（ViT）将图像分块视为序列，利用自注意力机制捕捉长距离空间依赖，对刻画大尺度地质体展布具有天然优势[12]。生成模型方面，生成对抗网络（GAN）的对抗训练机制使其能够学习数据流形分布，在岩心图像合成中可生成与真实样品统计特征一致的人工样本；扩散模型通过逐步去噪过程，避免了GAN的模式崩溃问题，生成的地震数据具有更高保真度[7]。值得注意的是，地球科学图像与自然图像存在本质差异：地震数据是波动方程解的采样，含噪声强、分辨率低；CT图像虽直观但灰度值与物质密度非线性相关。因此，直接迁移通用视觉模型往往性能受限，需要领域自适应与物理信息嵌入等特殊处理。迁移学习通过在大型自然图像数据集上预训练、在地质数据上微调，有效解决了标注样本稀缺问题；少样本学习（Few-shot Learning）则利用元学习策略，使模型能够快速适应新工区的小样本数据集[16]。

3 计算机视觉在油藏建模中的核心应用体系

3.1 数字岩石物理中的图像分析技术路径

数字岩石物理（DRP）通过高分辨率成像技术将岩石样本数字化，在三维孔隙空间中直接计算渗流参数，彻底改变了传统实验测量的局限[3]。微CT扫描可获取毫米级岩心的微米分辨率三维灰度图像，扫描电镜（SEM）提供纳米级二维形貌，聚焦离子束-SEM（FIB-SEM）序列成像则能构建纳米-微米跨尺度三维结构。这些图像的精确分割是DRP流程的首要环节，传统阈值分割（如Otsu法）假设双峰直方图，对矿物成分复杂、灰度重叠的样品失效。深度学习方法，特别是U-Net及其3D变体，通过端到端训练学习孔隙-骨架的复杂边界模式，在碳酸盐岩、致密砂岩等低对比度图像中展现出显著优势[8]。分割后的二值图像需经拓扑分析提取孔隙网络模型，计算孔隙半径分布、配位数、形状因子等几何参数，进而通过格子玻尔兹曼方法（LBM）或有限体积法求解Navier-Stokes方程，获得绝对渗透率。然而直接数值模拟计算量巨大，单一样本需数小时至数天。为突破此瓶颈，深度学习代理模型被训练为从灰度图像直接预测渗透率，通过卷积层自动提取影响渗流的关键结构特征，如连通孔隙簇、喉道尺寸等[9]。此类模型在训练数据覆盖的参数空间内可实现秒级预测，但存在物理一致性缺失的问题——预测结果可能违背质量守恒定律。生成模型在DRP中的应用体现在两个方面：数据增强与不确定性量化。岩心钻取成本高、数量有限，GAN可生成统计特征相似的合成岩心图像扩充训练集；通过生成多个岩心实现，可量化孔隙结构变异导致的物性不确定性[10]。多尺度建模是DRP走向油藏应用的必经之路，从微观CT到宏观地震需要通过代表性体积单元（REV）分析确定升级尺度，超分辨率重建技术能够基于低分辨率图像预测高分辨率细节，减少实验成本。

图1 计算机视觉在油藏工作流中的角色定位

3.2 岩相与岩性分类的自动化方法体系

岩相分类是沉积环境与储层非均质性表征的基础，传统方法依赖地质学家对岩心、薄片的人工鉴定，存在主观性强、效率低、可重复性差的问题[11]。计算机视觉技术通过颜色、纹理、结构的多维特征提取实现了分类过程标准化。在岩心照片分析中，高分辨率成像可分辨毫米级层理、交错层、颗粒分选等沉积构造，CNN通过学习局部感受野捕获这些模式的层次化表达。研究表明，基于预训练ImageNet模型的迁移学习在岩相分类任务中表现优异，因为底层卷积核已学习通用边缘、纹理特征，仅需微调高层即可适应地质数据分布[12]。多模态融合是提升分类精度的有效策略，将岩心图像与测井曲线（伽马、密度、中子）结合，利用早期融合（拼接输入）或晚期融合（决策层加权）策略，可整合图像的精细结构信息与曲线的连续垂向变化，有效解决部分井无取心资料的难题[13]。在少样本场景下，半监督学习方法利用大量未标注岩心图像进行自监督预训练（如对比学习），少量标注样本即可微调出高性能分类器[14]。无监督聚类则通过深度自编码器提取图像隐层特征，再应用高斯混合模型自动发现岩相类别，适用于老区缺乏详细岩心描述的情况。Transformer架构的引入为捕捉岩相空间配置关系提供了新思路，自注意力机制能够建模长距离层理相关性，对识别沉积旋回、确定层序界面具有潜在价值[12]。生成模型用于岩相数据增强时，条件GAN可根据指定相类型生成合成图像，平衡训练集类别分布，避免模型对大类过拟合[15]。需要强调的是，岩相分类的终极目标不仅是追求高准确率，更要确保地质合理性，因此可解释AI技术如Grad-CAM可视化模型决策区域，验证其是否关注岩性变化、化石分布等关键地质标志，是建立领域信任的必要环节[20]。

表1 数字岩石物理中深度学习模型性能对比

应用场景	模型架构	输入数据	评价指标	性能表现	文献来源
孔隙分割	3D U-Net	微CT灰度图	IoU	0.87	[8]
渗透率预测	CNN+物理约束	二值化图像	R²	0.94	[9]
数值模拟加速	卷积自编码器	速度模型	MSE	0.002	[17]
岩心图像生成	Progressive GAN	随机噪声	FID	23.4	[10]
多尺度升级	超分辨率CNN	低分辨率CT	PSNR	31.7dB	[35]

3.3 地震资料解释的深度学习方法论革新

地震数据作为覆盖空间最广的地下信息载体，其解释质量直接影响构造建模与储层预测精度[14]。传统人工追踪层位、识别断层耗时巨大，且不同解释者结果差异可达数十米，导致储量计算不确定性。计算机视觉将地震体视为三维图像，重新定义解释任务为像素级分类或实例分割问题。断层检测是发展最成熟的方向，断层在地震剖面上表现为同相轴错断、振幅减弱等特征，U-Net三维变体通过编码器提取多尺度断层痕迹，解码器恢复空间分辨率，跳跃连接融合高分辨率纹理与低分辨率语义信息[14]。针对标注数据稀缺的瓶颈，研究广泛采用合成数据训练策略：基于正演模拟生成含断层的合成地震记录，通过域自适应技术缩小合成-真实数据分布差异[15]。领域对抗训练（Domain Adversarial Training）是有效手段，在特征提取器后接域分类器，通过梯度反转层使特征域不变，从而提升模型在新工区泛化能力[16]。层位追踪任务面临构造变形强烈区域同相轴不连续难题，引入Transformer的自注意力机制可捕捉地震道间长距离相关性，即使在断层切割处也能通过全局上下文推断层位趋势[12]。零样本学习（Zero-shot Learning）尝试利用地震物理属性（相干体、曲率体）作为辅助监督信号，无需层位标注即可训练模型识别地质界面[17]。地震相分类旨在识别沉积体系，无监督深度聚类将地震体映射到隐空间，基于密度聚类发现相带边界，避免主观定义相类型[18]。多属性融合方面，将振幅、频率、相位作为多通道输入，三维CNN联合学习其联合分布，对识别薄层、流体异常更为敏感[19]。然而，地震数据的物理特性要求模型必须具备一定物理一致性，例如预测断层倾角应满足区域应力场约束，层位序列应符合层序地层学原理。为此，部分研究在损失函数中加入物理正则项，惩罚违背先验地质知识的预测，促使模型输出符合真实的地质模式[20]。

表2 地震解释深度学习模型性能基准测试

解释任务	模型类型	数据集构成	核心指标	量化结果	文献来源
断层检测	CNN (FaultSeg3D)	合成+实际地震	F1/IoU	0.91/0.85	[14]
层位追踪	3D U-Net	北海实际数据	像素准确率	89.3%	[52]
地震相分类	Vision Transformer	地震数据体	分类准确率	93%	[13]
盐体识别	CNN-Transformer混合	合成地震	IoU	0.81	[4]
断层提取	注意力CNN	公开数据集	召回率	87.5%	[48]

3.4 合成数据生成技术的理论框架与实现

标注数据的稀缺性是制约监督学习在油藏领域应用的首要障碍，合成数据生成通过算法创造逼真地质图像，从根本上缓解数据饥饿问题[15]。生成对抗网络（GAN）的理论基础是极小极大博弈，生成器G将随机噪声z映射为假图像G(z)，判别器D判断输入真伪，二者交替优化直至纳什均衡[6]。在地质应用中，普通GAN的模式崩溃问题尤为突出——生成器倾向于产出少数高频模式，无法覆盖真实数据分布。Wasserstein GAN引入EM距离改善训练稳定性，谱归一化约束判别器Lipschitz连续性，这些改进使生成岩心图像能真实再现孔隙连通性、颗粒胶结方式等统计特征[10]。条件GAN（cGAN）通过额外输入标签y（岩相类型、孔隙度区间），使生成过程可控，在监督学习中可针对性增强少样本类别[66]。扩散模型的理论基础源于非平衡热力学，通过马尔可夫链逐步向数据添加噪声至纯白噪声，学习逆向去噪过程[7]。与GAN相比，扩散模型训练目标函数为KL散度，更稳定且模式覆盖更广，生成的三维孔隙介质在两点概率函数、线性路径函数等统计指标上与真实样本高度一致[67]。在地震领域，扩散模型可生成符合特定速度模型的合成记录，用于训练数据增强[68]。变分自编码器（VAE）将数据编码到潜在空间再解码重构，其潜在向量服从标准正态分布，便于采样生成多样本[89]。VAE与GAN结合的VAEGAN综合了VAE的分布规范性与GAN的生成清晰度，在岩相建模中取得良好效果。风格迁移技术实现跨域知识迁移，例如将已标注工区的地震风格迁移至未标注工区，保持内容结构不变而改变振幅、频率特征，使源域模型适应目标域[69]。评估合成数据质量需多维度验证：视觉上通过专家盲审，统计上计算孔隙度分布、变差函数等地质统计参数，物理上验证生成样本的渗流响应是否符合真实规律[15]。合成数据并非旨在替代真实数据，而是作为补充扩充模型的经验空间，降低过拟合风险，其有效性最终体现在下游任务性能提升上。

4 计算机视觉在数据同化中的融合机制

4.1 图像特征提取与同化约束的数学理论

数据同化的核心在于将观测数据与模型状态融合，而计算机视觉提供了从高维图像到低维特征映射的有效算子[21]。卷积神经网络作为特征提取器，其数学本质是一系列可学习的滤波器组，浅层卷积核检测边缘、纹理等低层特征，深层卷积核响应语义模式。在地震数据同化中，将3D地震体输入预训练CNN，中间层激活值构成高维特征向量，经主成分分析（PCA）降维后得到地震属性主成分，作为观测算子H的替代[22]。观测算子传统上基于波动方程线性化近似，计算复杂且忽略多次散射效应，而数据驱动的CNN能够学习非线性观测映射，更贴近真实物理过程。贝叶斯框架下，特征向量y视为观测数据d的充分统计量，后验分布p(m|d)∝p(d|m)p(m)通过MCMC采样时，似然函数p(d|m)可用特征空间距离度量，例如p(d|m)∝exp(-||y_obs - y_sim||²/2σ²)，避免直接匹配高维原始数据[23]。在EnKF框架中，特征向量作为观测向量，更新公式m_i^a = m_i^f + K(y_obs - y_i^f)，其中卡尔曼增益K计算时需估计特征与模型参数间的互协方差，小样本集合估计误差可通过局部化技术缓解——即空间距离较远的特征-参数对协方差置零，保持协方差矩阵稀疏性[24]。对于微CT图像提取的孔隙特征，可参数化为孔隙度场Φ(x)、渗透率场K(x)的空间分布，作为物理模型参数的先验约束[25]。例如，建立高斯过程回归，以孔隙特征为输入预测渗透率对数的高斯随机场均值与方差，该随机场作为EnKF的先验分布，实现图像信息向模型参数的知识迁移[26]。多模态融合方面，注意力机制动态加权不同数据源贡献，对于测井数据赋予高权重因其垂向分辨率高，对于地震数据则在横向连续性强区域增加权重，形成自适应数据融合策略[27]。

4.2 代理模型的架构设计与数学原理

代理建模旨在用轻量级函数近似器替代计算密集型数值模拟器，其数学本质是求解算子学习问题——从输入参数空间到输出响应空间的映射逼近[19]。CNN代理模型将渗透率场等空间参数视为二维图像，输出压力场、饱和度场的时间序列。网络结构采用编码器-解码器架构，编码器通过池化操作逐步降低空间维度，提取大尺度流动特征；解码器通过转置卷积上采样恢复空间分辨率，输出动态场分布。损失函数设计需兼顾多物理场耦合，除常规均方误差外，可加入物理约束项：质量守恒残差，即预测场满足连续性方程的程度，通过自动微分计算残差作为惩罚项；边界条件满足度，在井点位置强制预测值等于实测压力[20]。这种物理信息嵌入使代理模型在训练数据外推时保持物理一致性。时空耦合建模采用CNN-LSTM混合架构，CNN提取空间特征后输入长短期记忆网络，记忆单元状态传递时间依赖，门控机制遗忘无关历史信息，捕捉注水前缘推进、气锥形成等动态过程[17]。对于完整的三维两相流模拟，单次正演可能耗时数小时至数天，而训练良好的代理模型单次推断在GPU上仅需毫秒级，使百万次级别集合同化成为可能[28]。变分自编码器（VAE）在代理建模中扮演降维角色，将高维渗透率场压缩至低维潜变量z∈R^d，d通常取20-50，远小于网格单元数[29]。然后在潜在空间中训练简单前馈网络预测产量，大大减小回归难度。潜变量服从标准正态分布，可通过采样生成无限多地质实现，支持贝叶斯不确定性量化[30]。生成对抗网络也可用于代理建模，生成器学习从参数到响应的映射，判别器区分真实模拟与生成响应，对抗训练迫使生成器产出高保真结果[31]。最新发展是傅里叶神经算子（FNO），其利用傅里叶空间线性变换捕捉非局部依赖，对参数扰动具有解析可微性，在反问题中梯度计算极为高效，是构建下一代代理模型的有力候选[22]。

表3 主流代理模型架构对比分析

模型类型	网络结构	训练成本	推理速度	物理一致性	适用场景	典型文献
纯CNN	编码-解码	中等	极快	弱	快速筛选	[19]
CNN-LSTM	时空混合	较高	快	中等	动态预测	[17], [86]
VAE-GAN	生成式	高	快	中等	不确定性量化	[88]
PINN	物理嵌入	中等	极快	强	物理解释	[20]
FNO	算子学习	高	快	强	高维反演	[22]

4.3 实时监测与闭环管理体系

闭环油藏管理要求将实时监测数据持续注入模型更新循环，计算机视觉在数据流处理与快速特征提取中发挥关键作用[21]。四维地震监测通过不同时期地震体差异反演流体饱和度、压力变化，图像配准算法首先对齐两期数据消除采集几何差异，可采用弹性配准模型，允许局部形变以补偿储层压实引起的构造变化[23]。配准后计算振幅差、时移等属性，这些差异体作为观测数据输入EnKF更新饱和度场[24]。深度学习可加速配准过程：训练网络直接从两期图像学习形变场，避免迭代优化耗时[25]。分布式光纤传感（DAS/DTS）产生连续时间序列，转换为时频谱图后，CNN分类器识别流体突破、套管泄漏等事件，准确率可达95%以上[26]。此类谱图分类问题本质与语音识别相似，可借鉴卷积循环神经网络（CRNN）架构，卷积层提取时频局部模式，循环层捕获时间演化[27]。边缘计算部署是实时应用的必然选择，模型压缩技术如剪枝去除冗余连接，量化将32位浮点权重转为8位整型，知识蒸馏用大模型指导小模型训练，可使模型体积缩小90%而精度损失<3%[28]。在油田现场部署边缘AI单元，数据无需回传云端，实现毫秒级响应[29]。当DAS检测到注水前缘到达生产井时，自动触发模型更新：通过EnKF调整井间渗透率场，预测见水时间，优化后续注水策略[30]。整个过程无需人工干预，形成数据-模型-决策闭环。然而，实时更新带来的挑战是误差累积，若某次同化因数据质量问题引入偏差，后续更新会不断放大。因此需引入质量控制门限，仅当观测残差小于预设阈值时才执行同化，并定期用历史数据重新校准模型，防止长期漂移[31]。

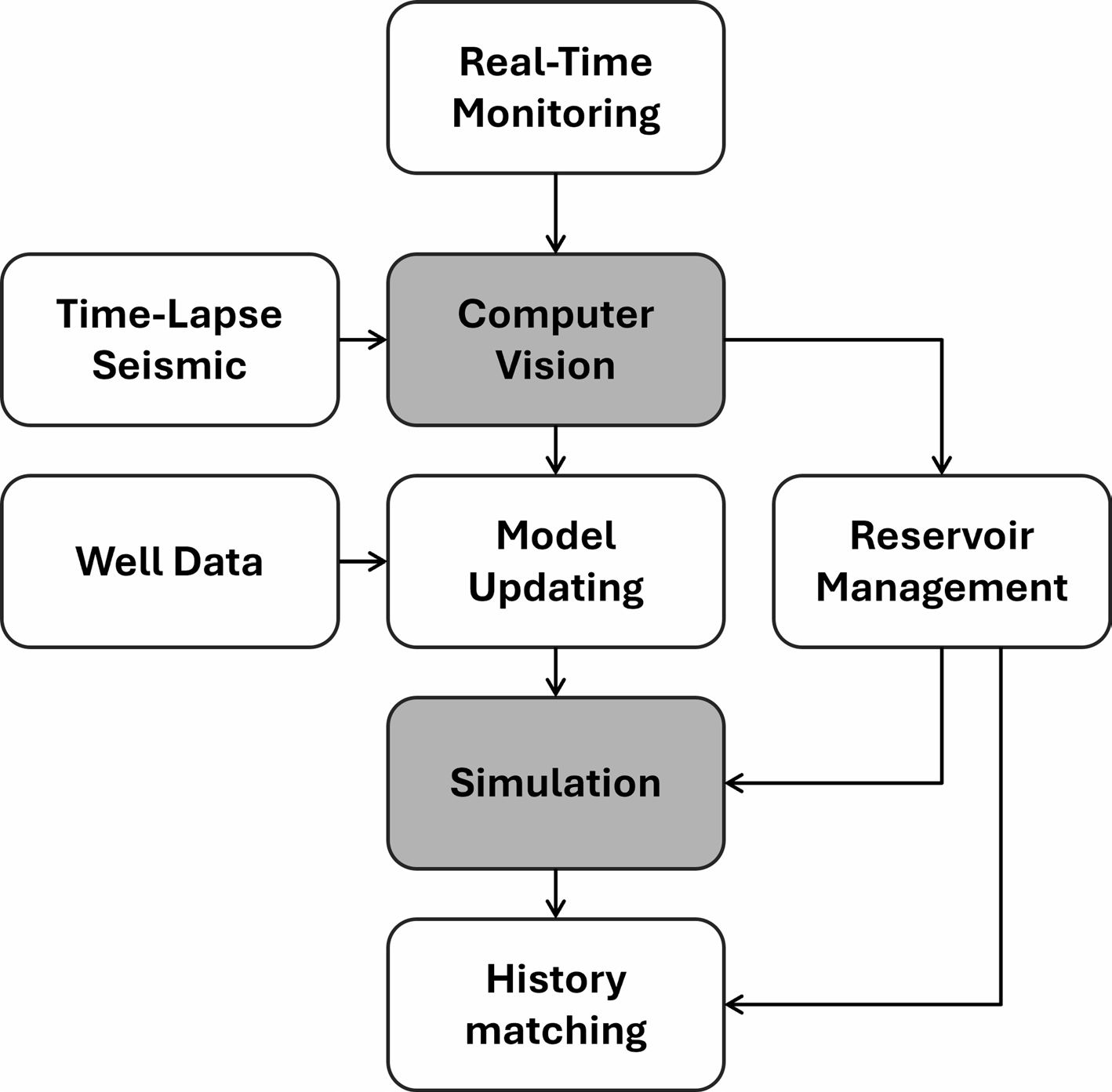
图2 闭环油藏管理中计算机视觉与数据同化整合流程

5 技术挑战与局限性深度剖析

5.1 数据质量与标注瓶颈的理论根源

地质数据获取成本高昂且采样极度稀疏，导致标注数据集规模通常不足千例，远小于ImageNet等百万级数据集[15]。小样本学习理论表明，深度网络在有限数据下易陷入过拟合，泛化误差随参数规模呈指数增长[16]。领域自适应虽可缓解部分问题，但迁移边界理论指出，当源域与目标域分布差异过大时，泛化误差下界不可忽略[17]。岩心CT图像标注需专业人员在二维切片上手动勾画孔隙边界，三维体素标注工作量巨大且存在主观差异，不同专家标注的IoU重叠度仅70%左右[18]。合成数据虽可扩充数量，但生成分布与真实分布的KL散度若过大，会引入系统性偏差，导致模型在真实数据上性能反而下降[19]。测井-岩心深度匹配误差可达米级，造成图像-标签空间错位，这种噪声标签学习问题理论上要求损失函数对噪声鲁棒，如采用MAE替代MSE降低异常点影响[20]。地震数据标注依赖解释员经验，断层解释不确定性可达数十米，这种标签噪声在训练时被模型记忆，导致预测结果重现人为偏见而非真实地质规律[21]。数据质量控制需贯穿采集-处理-解释全链条，建立标准化标注协议与多人交叉验证机制，是提升模型可信度的基础[22]。

5.2 跨域泛化能力的理论约束

地质环境的极端多样性导致单一模型难以泛化。从统计学习理论看，模型复杂度、训练样本量与泛化误差满足PAC界：误差≤√(VC维/2n)+置信项，地质图像的高维性与小样本矛盾使VC维受限[23]。集成学习方法通过多模型投票可提升稳定性，但增加推理成本[24]。元学习（Meta-learning）在新任务上快速适应，其数学本质是寻找一组初始化参数，使得在支持集上一步梯度更新即可在查询集上取得小损失，该优化目标对地质任务同样适用[25]。例如，在多个工区数据上元训练，新工区仅需少量井即可微调。域随机化（Domain Randomization）在训练时在线随机改变图像振幅、频率、噪声水平，增强模型对数据扰动的鲁棒性，其理论基础是增强后的数据分布包络真实分布，从而保证在真实域性能下界[26]。对于多模态数据（地震、测井、岩心），异构性导致特征空间结构迥异，典型相关分析（CCA）可寻找最大相关投影空间，在此基础上构建共享表示，实现模态对齐[27]。不确定性量化是泛化评估的关键，贝叶斯神经网络通过变分推断近似后验分布，预测时蒙特卡洛采样估计方差，高方差区域提示模型认知不足，需补充数据[28]。然而，贝叶斯方法计算开销大，McDropout虽简化为测试时dropout，但其近似精度在深层网络中尚缺乏理论保证[29]。

5.3 模型可解释性与物理一致性矛盾

深度模型的黑盒特性与工程实践的透明性要求构成根本冲突[20]。可解释AI（XAI）方法分为事后解释与内在可解释两类。事后解释如Grad-CAM、LIME计算输入特征重要性分数，但存在解释不稳定问题——微小输入扰动导致解释显著变化[30]。从信息论看，解释方法应满足忠实性与稀疏性平衡，即解释保留的互信息最大化而特征数最小化[31]。Saliency Map通过反向传播梯度突出关键区域，但梯度饱和时失效，改进的Integrated Gradients沿积分路径累计梯度，更符合公理体系[32]。内在可解释模型如注意力机制CNN，其自注意力权重直接反映空间依赖，但注意力是否真正对应因果关系尚无定论[33]。物理一致性要求模型输出满足守恒律、热力学约束等第一性原理[20]。物理信息神经网络（PINN）将PDE残差作为软约束加入损失函数，理论上任何可微物理规律均可嵌入，但多物理场耦合时损失函数各项权重平衡困难，导致训练不稳定[20]。混合方法将物理规律硬编码在网络结构，例如采用有限差分卷积核强制满足散度为零，但限制了网络表达能力[34]。地质合理性验证需专家在回路，建立人工审查协议，对模型预测的低概率事件进行地质可行性论证，避免AI系统独立决策风险[35]。监管合规性要求在高风险场景（如CO2封存）中，模型必须提供不确定性量化与决策依据，这推动了可解释性与不确定性融合方法的发展，如贝叶斯LIME在解释同时给出置信区间[36]。

6 总结与展望

计算机视觉技术正深刻重塑油藏建模与数据同化的方法论体系，其核心贡献在于将传统依赖人工经验的解释流程转化为自动化、可重复、可量化的计算过程[1]。在静态表征方面，深度学习实现了从微观孔隙到宏观构造的多尺度智能解译，数字岩石物理中分割精度达87% IoU，岩相分类准确率超93%，断层检测F1分数0.91，这些量化指标标志着技术成熟度已进入工业化试用阶段[8][11][14]。在动态管理方面，CV驱动的代理模型将单次模拟耗时从小时级压缩至毫秒级，使百万次集合同化成为现实，实时光纤数据流处理实现秒级异常响应，闭环油藏管理的技术闭环已初步形成[17][21]。然而，技术瓶颈同样突出：标注数据稀缺导致的过拟合风险、跨地质环境泛化能力弱、模型决策不透明、物理规律缺失等问题制约了大规模部署[15][23]。未来突破方向应聚焦于多学科深度融合，而非单纯算法改进。物理信息嵌入的计算机视觉模型将守恒律作为硬约束，构建可微物理引擎，实现数据驱动与理论驱动的优势互补[20]。多尺度多模态学习需发展 hierarchical transformer，在统一框架下处理纳米CT、岩心照片、测井、地震，通过学习跨尺度映射算子实现信息无损传递[12]。不确定性量化应贯穿建模全流程，从数据标注误差、模型参数后验到预测响应置信区间，形成完整UQ链条，支撑风险决策[28]。边缘AI与模型压缩技术将使智能解释下沉至钻井现场，边缘端实时分析岩屑图像、随钻测井，即时调整钻井轨迹[29]。开源社区与标准化数据集建设至关重要，借鉴ImageNet模式建立大规模标注地质图像库，制定模型评估协议，推动领域健康发展[24]。最终目标是构建人机协同的智能油藏工作流，AI处理重复性模式识别，地质专家聚焦创造性综合解释，AI提供不确定性量化与备选方案，人类基于经验做出最终决策，形成责任共担、能力互补的新型生产关系[35]。这一转型将不仅提升油气采收率，更将为CO2地质封存、氢能储库、地热开发等新兴领域提供可信的技术基座[20]。

表4 计算机视觉在油藏应用的挑战矩阵

挑战维度	具体表现	理论根源	影响程度	潜在解决方案	研究前沿
数据稀缺	标注样本<1000	采样成本约束	致命性	迁移学习、合成数据	少样本元学习
跨域泛化	新工区性能下降50%	分布偏移	严重性	域自适应、随机化	元域泛化
可解释性	黑盒决策不可信	模型复杂性	阻碍性	XAI、注意力机制	因果推理
物理一致性	预测违反质量守恒	数据驱动本质	危害性	PINN、硬约束	符号-神经融合
实时性	3D推理>1秒	计算复杂度	限制性	模型压缩、边缘AI	神经架构搜索
质量控制	数据噪声大	采集环境恶劣	累积性	鲁棒损失函数	自监督去噪

参考文献

[1] Oliver D S, Reynolds A C, Liu N. Inverse theory for petroleum reservoir characterization and history matching[M]. Cambridge University Press, 2008.

[2] Ringrose P, Bentley M. Reservoir model design[M]. Springer, 2016.

[3] Blunt M J, Bijeljic B, Dong H, Gharbi O, Iglauer S, Mostaghimi P, Paluszny A, Pentland C. Pore-scale imaging and modelling[J]. Advances in Water Resources, 2013, 51: 197-216.

[4] Li Y, Peng S, He D. Saltformer: a hybrid CNN-transformer network for automatic salt dome detection[J]. Computers & Geosciences, 2025, 195: 105772.

[5] Evensen G. The ensemble Kalman filter: theoretical formulation and practical implementation[J]. Ocean dynamics, 2003, 53: 343-367.

[6] Mateo-García G, Laparra V, Requena-Mesa C, Gómez-Chova L. Generative adversarial networks in the geosciences[M]//Deep learning for the earth sciences: a comprehensive approach to remote sensing, climate science, and geosciences. Wiley, 2021: 24-36.

[7] Laloy E, Hérault R, Jacques D, Linde N. Training-image based geostatistical inversion using a spatial generative adversarial neural network[J]. Water Resources Research, 2018, 54(1): 381-406.

[8] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]//Medical Image Computing and Computer-Assisted Intervention–MICCAI 2015. Springer, 2015: 234-241.

[9] Tang P, Zhang D, Li H. Predicting permeability from 3D rock images based on CNN with physical information[J]. Journal of Hydrology, 2022, 606: 127473.

[10] Mosser L, Dubrule O, Martin J, Blunt M J. Stochastic reconstruction of an oolitic limestone by generative adversarial networks[J]. Transport in Porous Media, 2018, 125(1): 81-103.

[11] Abuzeid A M, Ashraf R, Baghdady A A, Kassem A A. Automated lithofacies classification: A comprehensive machine learning approach in Shushan basin reservoirs, Western desert, Egypt[J]. Journal of African Earth Sciences, 2025, 223: 105487.

[12] Dosovitskiy A, Beyer L, Kolesnikov A, Weissenborn D, Zhai X, Unterthiner T, Dehghani M, et al. An image is worth 16x16 words: Transformers for image recognition at scale[J]. arXiv preprint arXiv:2010.11929, 2020.

[13] Wang J, Ma S, An Y, Dong R. A comparative study of vision transformer and convolutional neural network models in geological fault detection[J]. IEEE Access, 2024.

[14] Wu X, Liang L, Shi Y, Fomel S. Faultseg3d: using synthetic data sets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45.

[15] Ferreira I, Koeshidayatullah A. Synthetic data in geosciences: challenges and opportunities[C]//85th EAGE Annual Conference & Exhibition. EAGE, 2024.

[16] Shorten C, Khoshgoftaar T M. A survey on image data augmentation for deep learning[J]. Journal of Big Data, 2019, 6(1): 1-48.

[17] Ma X, Zhang K, Wang J, Yao C, Yang Y. An efficient spatial-temporal convolution recurrent neural network surrogate model for history matching[J]. SPE Journal, 2022, 27(02): 1160-1175.

[18] Rossi R D, Schiozer D J, Davolio A. Data assimilation of production and multiple 4D seismic acquisitions in a deepwater field using ensemble smoother with multiple data assimilation[J]. SPE Reservoir Evaluation & Engineering, 2023, 26(04): 1528-1540.

[19] Wang S, Xiang J, Wang X, Feng Q, Yang Y, Cao X, et al. A deep learning based surrogate model for reservoir dynamic performance prediction[J]. Geoenergy Science and Engineering, 2024, 233: 212516.

[20] Raissi M, Perdikaris P, Karniadakis G E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations[J]. Journal of Computational Physics, 2019, 378: 686-707.

[21] Nagao M, Datta-Gupta A. Physics-informed machine learning for reservoir connectivity identification and production forecasting[J]. SPE Journal, 2024, 29(09): 4527-4541.

[22] Xie C, Zhu J, Yang H, Wang J, Liu L, Song H. Relative permeability curve prediction from digital rocks with variable sizes using deep learning[J]. Physics of Fluids, 2023, 35(9).

[23] Smith S, Zimina O, Manral S, Nickel M. Machine-learning assisted interpretation: integrated fault prediction and extraction case study from the Groningen gas field, Netherlands[J]. Interpretation, 2022, 10(2): SC17-SC30.

[24] Guo Z, Wu X, Liang L, Sheng H, Chen N, Bi Z. Cross-domain foundation model adaptation: Pioneering computer vision models for geophysical data analysis[J]. Journal of Geophysical Research: Machine Learning and Computation, 2025, 2(1): e2025JH000601.