NJU 凸优化导论(3) Convex Sets 凸集（上）仿射集、凸集、保持凸性的运算

https://www.lamda.nju.edu.cn/chengq/optfall24/slides/Lecture_3.pdf

目录

1.Affine and Convex Sets：仿射集与凸集

2.Operations That Preserve Convexity：保持凸性的运算

2.1 Intersection 交集

2.2 Affine function 仿射函数  

2.3 Perspective function 透视函数

2.4 线性分式函数

---

1.Affine and Convex Sets：仿射集与凸集

1.Lines x1与x2连线 两个写法（两个点 / 一个点向另一个点方向延伸）

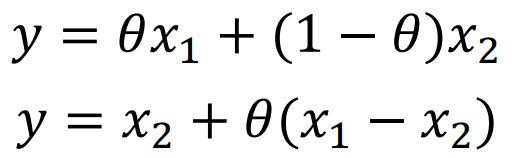
  时为线段

2.Affine Sets仿射集      集合包含 集合内部任意两点所连直线。

一条直线 一个平面都是仿射集。

k个点则为仿射组合 对θ范围没要求 只是k个和为1

  

3.subspace子空间 对加法和数乘封闭 

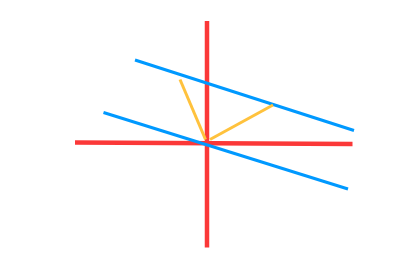
仿射集由子空间平移x0得到。 子空间是偏移量为0的仿射集。

比如 一条不过原点的直线，移动到过原点 就变成子空间。这个平移值x0不是固定的，只要移动过原点即可。

黄色为进行平移的方式 是不固定的x0 但得到的V 都是这样的过原点的直线。

4.线性方程组的解集是仿射集，每个仿射集都能表示为线性方程组的解集

5.Affine hull 仿射包 最小的包含C的仿射集

比如不共线的三个点 仿射包就是 这三点确定的平面；为2维。 

6. Convex Sets 凸集  和为1&系数非负

  

仿射要求所有的θ都满足 条件更强。 所有的仿射集都是凸集。

凸组合   

  凸包 

7.锥