B站吴恩达深度学习视频笔记（11）——多样本梯度下降和向量化处理多批次数据

前言

多样本梯度下降原理和单样本是一样的，只不过使用了代价函数——样本集中每个样本对应损失函数的平均值。而向量化对于深度学习处理数据速度的提升是非常大的，我们结合刚刚的多样本梯度下降讲一下向量化。

m 个样本的梯度下降和向量化处理数据

在之前的笔记中,已经讲述了如何计算导数，以及应用梯度下降在逻辑回归的一个训练样本上。现在我们想要把它应用在m个训练样本上。

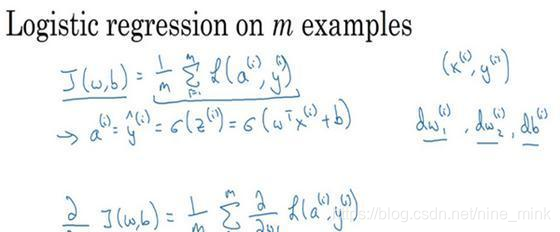
首先，让我们时刻记住有关于损失函数就J(w,b) 的定义。

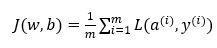
当你的算法输出关于样本y 的 a(i)， a(i)是训练样本的预测值，即：

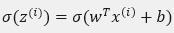
所以我们在前面展示的是对于任意单个训练样本，如何计算微分当你只有一个训练样本。

因此dw_1，dw_2和db 添上上标i表示你求得的相应的值。

如果你面对的是我们在之前演示的那种情况，但只使用了一个训练样本(x^(i),y(i)) 。

现在你知道带有求和的全局代价函数，实际上是1到m项各个损失的平均。

所以它表明全局代价函数对w1的微分，w1的微分也同样是各项损失对w1微分的平均。

但之前我们已经演示了如何计算这项，即之前幻灯中演示的如何对单个训练样本进行计算。

所以你真正需要做的是计算这些微分，如我们在之前的训练样本上做的。并且求平均，这会给你全局梯度值，你能够把它直接应用到梯度下降算法中。

所以这里有很多细节，但让我们把这些装进一个具体的算法。同时你需要一起应用的就是逻辑回归和梯度下降。

我们初始化 J=0,dw_1=0,dw_2=0,db=0

代码流程：

   J=0;dw1=0;dw2=0;db=0;
    for i = 1 to m
         z(i) = wx(i)+b
         a(i) = sigmoid(z(i)