费马点+模拟退火。。。今天yzc无聊说的。。。
每次向最远点反向挪。。长度退火。。。
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<functional>
#include<iostream>
#include<cmath>
#include<cctype>
#include<ctime>
using namespace std;
#define For(i,n) for(int i=1;i<=n;i++)
#define Fork(i,k,n) for(int i=k;i<=n;i++)
#define Rep(i,n) for(int i=0;i<n;i++)
#define ForD(i,n) for(int i=n;i;i--)
#define RepD(i,n) for(int i=n;i>=0;i--)
#define Forp(x) for(int p=pre[x];p;p=next[p])
#define Lson (x<<1)
#define Rson ((x<<1)+1)
#define MEM(a) memset(a,0,sizeof(a));
#define MEMI(a) memset(a,127,sizeof(a));
#define MEMi(a) memset(a,128,sizeof(a));
#define INF (2139062143)
#define F (100000007)
#define MAXN (100+10)
#define eps 1e-10
long long mul(long long a,long long b){return (a*b)%F;}
long long add(long long a,long long b){return (a+b)%F;}
long long sub(long long a,long long b){return (a-b+(a-b)/F*F+F)%F;}
typedef long long ll;
long double sqr(long double x){return x*x;}
struct P
{
long double x,y,z;
P(){x=y=z=0;}
P(long double _x,long double _y,long double _z):x(_x),y(_y),z(_z){}
friend long double dis(P a,P b){return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y)+sqr(a.z-b.z));}
friend P operator+(P a,P b){return P(a.x+b.x,a.y+b.y,a.z+b.z);}
}a[MAXN],st;
struct V
{
long double x,y,z;
V(){x=y=z=0;}
V(long double _x,long double _y,long double _z):x(_x),y(_y),z(_z){}
V(P a,P b):x(b.x-a.x),y(b.y-a.y),z(b.z-a.z){}
friend V operator+(V a,V b){return V(a.x+b.x,a.y+b.y,a.z+b.z);}
friend V operator*(V a,long double b){return V(a.x*b,a.y*b,a.z*b); }
};
P operator+(P a,V b){return P(a.x+b.x,a.y+b.y,a.z+b.z);}
int n;
int main()
{
//freopen("CF106E.in","r",stdin);
cin>>n;
For(i,n) cin>>a[i].x>>a[i].y>>a[i].z,st=st+a[i];
st.x/=n,st.y/=n,st.z/=n;
long double step=1;
while (step>eps)
{
int p=1;
Fork(i,2,n)
if (dis(st,a[i])>dis(st,a[p])) p=i;
st=st+V(st,a[p])*step;
step*=0.999;
}
//cout.setf(ios::fixed);
//cout.precision(2);
cout<<st.x<<' '<<st.y<<' '<<st.z<<endl;
return 0;
}







 本文介绍了一种使用费马点和模拟退火方法来确定银河系中最佳救援站位置的技术。该方法通过不断调整候选位置使其远离最远行星的距离最小化。
本文介绍了一种使用费马点和模拟退火方法来确定银河系中最佳救援站位置的技术。该方法通过不断调整候选位置使其远离最远行星的距离最小化。
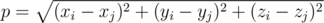 .
The rescue station can be positioned in any point in the space. It can also coincide with some planet.
.
The rescue station can be positioned in any point in the space. It can also coincide with some planet.















 2557
2557

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








