Java哈希表

什么是哈希

在顺序存储结构或者是链式存储结构中，元素关键码与其存储的位置之间没有明显的对应关系。因此在查找一个元素的时候， 需要和其他元素进行多次比较，顺序存储结构的查找时间复杂度为O(n)，链式存储结构中，平衡树的查找时间复杂度可以达到O()。

如果可以不经过比较，就可以获得想要搜索的元素，那么查找的时间复杂度就可以降低到O(1)。构造一种数据结构，可以让元素存储的位置和它的关键码之间能够建立映射关系，那么就可以很快的查找到该元素。

该方法就称为哈希方法（散列）

哈希函数

hash(key) = key % capacity

• 其中key关键码

• capacity为存储元素底层空间的总大小

如何使用这个哈希函数？

例如，这里有一组数据{1，7，6，4，5，9}

利用哈希函数，可以得到如下：

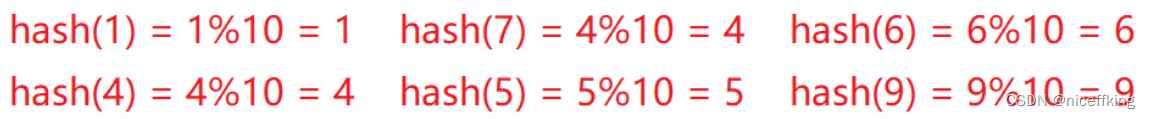
通过哈希函数计算，获得的hash值就为该数据存放的地址：

Hash冲突

什么是冲突

例如哈希函数：hash(key) = key % capacity进行插入一定不会出现问题吗？

如果还是用这组数据：{1，7，6，4，5，9}，然后向里面插入11会如何？

如果要插入11，利用哈希函数，可以得到hash(11) = 11 % 10 = 1

这个结果和插入1 ： hash(1) = 1 % 10 = 1 得到了相同的哈希地址，但是1下标这个位置已经被数据“1”所占据,那么该如何处理这种情况？

为什么会冲突

使用hash存储数据的时候，难免会有多个相同hash地址的数据，但是他们不可能存放在同一个hash地址上，这种冲突就不可避免的产生了。

我们称这种具有相同的哈希地址的数据元素为“同义词”，这种冲突现象我们称之为哈希冲突或者哈希碰撞

这种冲突是必然的，我们不可能完全避免，只能尽量做到降低冲突的概率。

如何降低冲突率

引起哈希冲突的原因可能是哈希函数设置的不合理, 哈希函数的设计应该遵循一些原则:

• 哈希函数的定义域必须包含需要存储的全部关键码, 如果散列允许有m个地址的时候, 其值域必须在0到(m-1)之间

• 哈希函数计算出来的地址能均匀的分布在整个空间之中, 而不是集中在一个地址

• 哈希函数设计和计算起来应该更加的简单

常用的解决冲突的方法:

1. 直接定制法:

去关键字的某个线性函数为散列地址

哈希函数为: Hash(key) = A* key + B;

优点: 简单, 均匀.

缺点,:需要实现知道数据的分布情况.

2. 除留余数法:

设散列地址数位m, 去一个不大于m的数, 但是最接近或者等于m的质数 p作为除数

哈希函数为: Hash(key) = key % p

3. 平方取中法:

假设关键字为1234，对它平方就是1522756，抽取中间的3位227作为哈希地址； 再比如关键字为4321，对它平方就是18671041，抽取中间的3位671(或710)作为哈希地址 平方取中法比较适合：不知道关键字的分布，而位数又不是很大的情况.

还有开放地址法和分离链接法等等, 下面会详细讲解最常用的开放地址法.

负载因子

散列表负载因子的定义为: fac = 填入表中的元素个数 / 散列表的长度

也就是说, 负载因子fac是散列表装满程度的表示方法, 由于表长度时定值, 当填入表中的元素个数越多, 或者散列表的长度越短的时候, 表名表的装满程度就越大, 产生冲突的可能性就越大, 反之越小, 所以解决哈希冲突的办法就是尽量去降低负载因子.

开放地址法

线性探测

如果我们使用哈希函数hash(key) = key % 10, 如果现在有一个数据4 和14需要存储到散列表当中去, 那么毫无疑问的他们会产生冲突, 所以我们就把14 放在4的地址的右边一位:

这样就解决了冲突, 同理如果有个数据是44, 那么就把他放在14后面, 以此类推, 这个被称为线性探测

缺点: 如果我们要查找的话就会非常的麻烦, 如果要删除呢? 例如, 如果直接删除4 , 那么44 的查找就会很麻烦, 如果使用hash函数去查找44, 它首先是去查找4这个值, 发现这个地方没有值则会直接认为44不存在.

二次探测

为了解决线性探测带来的问题, 我们采用以下哈希函数:

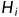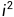= ( + ) % m

例如: 在已经插入4的情况下, 插入14, 24,44. 插入14的时候为第一次冲突, i = 1, h0 = 4, 所以hash值为 5, 以此类推.

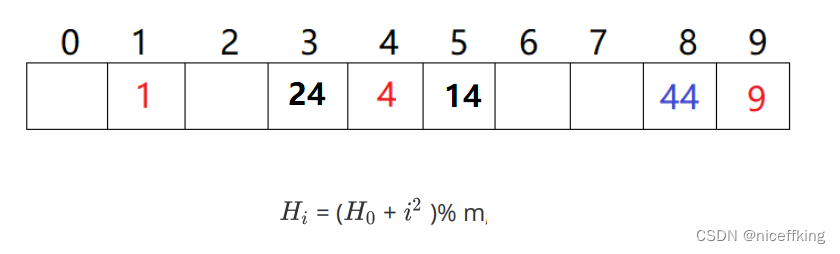
链地址法

原理

如果每一个地址只能存放一个值的话, 那么势必会有地址冲突的种情况, 对于二次探测这种方法, 也难免会造成空间浪费的情况, 而且空间的利用度也很低.

接下来介绍的这种链地址法, 来解决上述的问题:

原理, 也就是设置一个数组, 数组里面存放着一个类, 这个类里面包含着哈希地址和一个链表的头节点, 这个链表里面存放着 等于这个数组里面类对应哈希地址的哈希值, 例如:

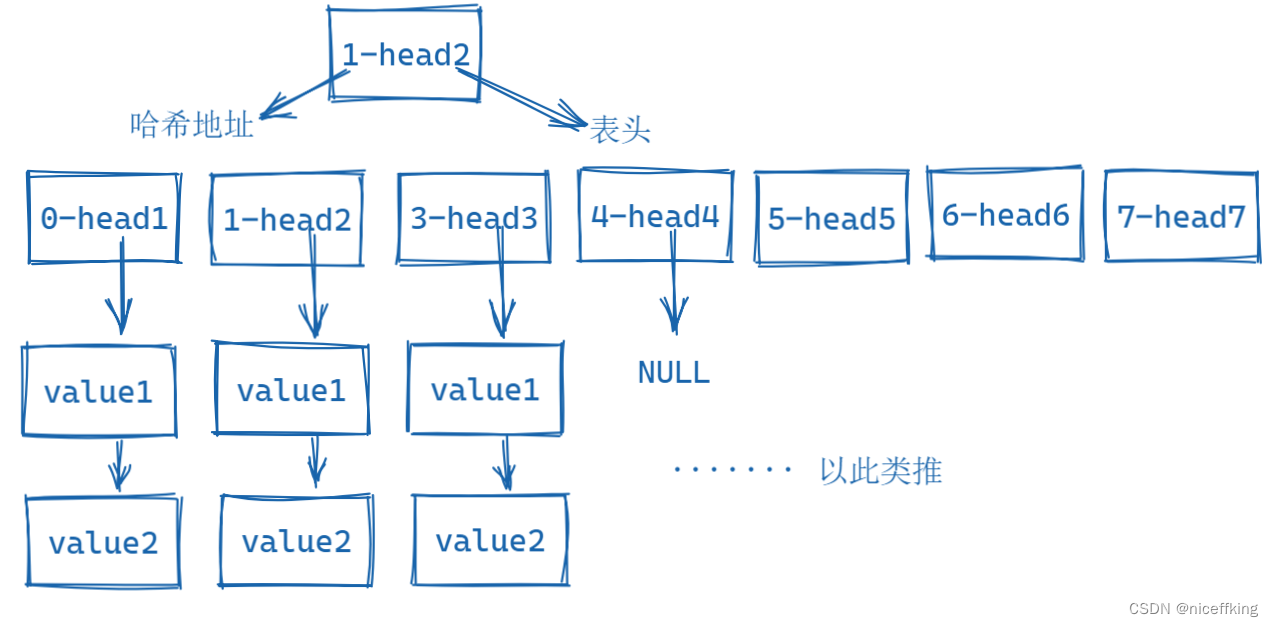
实现

1. 构造一个哈希类

public class HashBack {
    // 内部类
    static class Node {
        public int key;
        public int value;
        public Node next;

        public Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }
    public Node[] arr;
    public int usedSize; 
    
    // 负载因子
    public static final double LOADFACTOR = 0.75;
}

2. put方法

public void put(int key, int val) {
        int index = key % arr.length;
        Node cur = arr[index];
        while(cur != null) {
            if (cur.key == key) {
                cur.value = val;
                return;
            }
            cur = cur.next;
        }
        Node tem = new Node(key, val);
        tem.next = cur;
        arr[index] = tem;
        usedSize++;

        if (calculateLoadFactor() >= LOADFACTOR) {
            reSize();
        }
    }

3. get方法

    public int get(int key) {
        int index = key % arr.length;
        Node cur = arr[index];
        while ( cur != null) {
            if (cur.key == key) {
                return cur.value;
            }
        }
        return -1;
    }

4. 计算负载因子

    // 计算负载因子
    private double calculateLoadFactor() {
        return usedSize * 1.0 / arr.length;
    }

5. reSize方法(扩容)

扩容的时需要注意将原有key重新排列如新的数组当中

    void reSize() {
        Node[] newArr = new Node[2 * arr.length];
        for(int i = 0; i < arr.length; i++) {
            Node cur = arr[i];
            while(cur != null) {
                Node curNext = cur.next;
                int index = cur.key % newArr.length; // 找到了在新的数组当中位置
                cur.next = newArr[index];
                newArr[index] = cur;
                cur = curNext;
            }
        }
        arr = newArr;
        System.out.println("扩容成功");
    }

6.总览

public class HashBack {
    static class Node {
        public int key;
        public int value;
        public Node next;

        public Node(int key, int value) {
            this.key = key;
            this.value = value;
        }
    }
    public Node[] arr;
    public int usedSize;

    public static final double LOADFACTOR = 0.75;

    // 构造方法
    public HashBack() {
        arr = new Node[10];
    }

    // 扩容

    /**
     * 这地方需要对所有的因子进行重组
     * @return
     */
    void reSize() {
        Node[] newArr = new Node[2 * arr.length];
        for(int i = 0; i < arr.length; i++) {
            Node cur = arr[i];
            while(cur != null) {
                Node curNext = cur.next;
                int index = cur.key % newArr.length; // 找到了在新的数组当中位置
                cur.next = newArr[index];
                newArr[index] = cur;
                cur = curNext;
            }
        }
        arr = newArr;
        System.out.println("扩容成功");
    }

    // 插入
    public void put(int key, int val) {
        int index = key % arr.length;
        Node cur = arr[index];
        while(cur != null) {
            if (cur.key == key) {
                cur.value = val;
                return;
            }
            cur = cur.next;
        }
        Node tem = new Node(key, val);
        tem.next = cur;
        arr[index] = tem;
        usedSize++;

        if (calculateLoadFactor() >= LOADFACTOR) {
            reSize();
        }
    }

    // 计算负载因子
    private double calculateLoadFactor() {
        return usedSize * 1.0 / arr.length;
    }

    //get方法
    /**
     * 获取
     */
    public int get(int key) {
        int index = key % arr.length;
        Node cur = arr[index];
        while ( cur != null) {
            if (cur.key == key) {
                return cur.value;
            }
        }
        return -1;
    }
}

对于class类型的key参数

我们可以使用泛型来修改这个实现, 对于单个类的对象, 我们需要重写hashCode方法和equals方法.

性能分析

在实际使用过程中，我们认为哈希表的冲突率是不高的，冲突个数是可控的，也就是每个桶中的链表的长度是一个常数，所以，通常意义下，我们认为哈希表的插入/删除/查找时间复杂度是O(1)

实际应用

oj练习:

使用

1. 只出现一次的数字

2. 复制带随机指针的链表

3. 宝石与石头

4. 坏键盘打字

5. 前K个高频单词

其中1235为leetcode, 4为牛客.