编译原理：短语、直接短语和句柄

概念：

如果Ｓ->* αＡβ and A->+γ，则称γ是句型αγβ的相对于变量A的短语
如果Ｓ->* αＡβ and A->γ，则称γ是句型αγβ的相对于变量A的直接（简单）短语，最左直接短语叫做句柄

一般画出语法树来判断

判断方法：一个句型的语法树中任一子树叶结点所组成的符号串都是该句型的短语；

                  当子树中不包含其他更小的子树时，该子树叶结点所组成的字符串就是该句型的直接（简单）短语；

                  一个句型的最左直接短语汇称为该句型的句柄。

每棵语法树的叶子结点从左到右排列构成一个句型 
每棵语法树的子树的叶子结点从左到右排列构成一个短语 
每棵语法树的简单子树（只有父子两层结点）的叶子结点从左到右排列构成一个简单(直接)短语 

例题：

已知文法

E→T| E+T | E-T

T→F| T*F |T/F

 F→(E) | i

请写出该文法句型T+T*F+i的短语，直接短语和句柄。

先画出语法树：

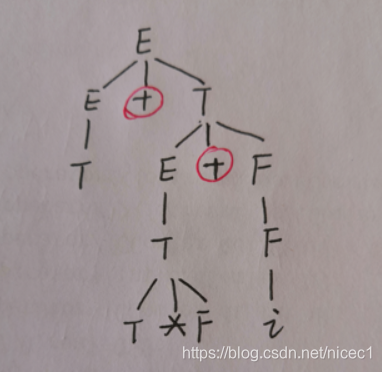
判断短语： 

1. 对于第一层的非终结符 E ，其叶节点所组成的短语是 T + T*F + i 
2. 对于第二层的非终结符 E，其叶节点所组成的短语是 T
3. 对于第二层的非终结符 T，其叶节点所组成的短语是 T*F + i
4. 对于第三层的非终结符 E ，其叶节点所组成的短语是 T*F
5. 对于第三层的非终结符 F ，其叶节点所组成的短语是 i
6. 对于第四层的非终结符 T，其叶节点所组成的短语是 T*F
7. 对于第五层的非终结符 F ，其叶节点所组成的短语是 i

 所以短语有：T+T*F+i , T*F+i , T , T*F , i 

图中画圈的“+”号，虽然是叶子结点，但是他的父节点所在子树不是简单子树

直接短语： T , T*F , i

句柄：T